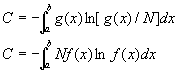
§
7.5连续变量的复杂程度公式 我们对广义集合的分析以标志值为离散取值的情况为主线。这符合当代的所谓“数字化”(现代很多电子产品广告中所谓的数字化实际是指用离散量代替连续变化的模拟量)潮流,而公式简单含义清楚也是原因。但是这并不表示对广义集合的分析仅对离散变量适用。实际上弄清了离散情况的问题以后处理连续变化的标志值也很方便。这里引出标志值为连续变量情况下的复杂程度的公式。 前面求代数平均值时曾经用g(x)表示对应的密度分布函数;用f(x)表示相对密度分布函数。即标志值x有单位增量时个体个数的增量。g(x)与Δx的乘积对应于标志值出现于x→x+Δx区间时个体的数量;f(x)Δx对应于标志值出现于x→x+Δx区间时个体数量增加的百分比(概率),参照离散情况时复杂程度公式(7.5),可以类比地得到标志值(变量)连续情况时的复杂程度公式应当是(关于处理中某些数学问题与物理思考在第九章中说明)。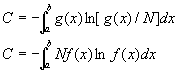
很显然,如果已经知道了连续的分布函数的数学表达式,而且可以做积分,就可以得到一个具体的计算复杂程度的公式。这些公式在下一篇中我们会适当介绍。所以连续变量的复杂程度的计算示例在这里也不介绍了。
§7.6讨论和小结| 大家都熟悉平均值,但是指出过去计算的那些平均值都是对应的广义集合的每个个体的标志值的平均值则是我们新认识。用广义集合多项式计算平均值也是新认识。 | |
| 本章从算术平均值、几何平均值、调和平均值进而引出从一种特殊的平均值。它由广义集合的分布函数计算出来,恰好有能力描写一个广义集合的内部发状态的丰富程度、标志值的差异程度(在某些场合也被称为混乱程度、无序程度)。我们称它为复杂程度。这种对复杂程度的定义与人们对“复杂”的理解是一致的。 | |
| 计算复杂程度的公式是(7.5)和(7.7),它们并不复杂。它们也是本书使用最多的公式。 | |
| 如果各个个体的标志值都相同,该广义集合的复杂程度为零。如果各个个体的标志值都不同,其复杂程度C的公式简化为C=NlogN 。N是广义集合内个体的总个数。 | |
| 复杂程度的计算单位与现在计算机界、信息论中广泛使用的计量信息的单位比特(Bit)等单位是一致的。 | |
复杂程度也可以看成是广义集合内不同的标志值在随机抽样中被抽中的概率的一种特殊的平均值。 | |
| 人们围绕平均值已经做过很多工作了。现在发现一切可以计算平均值的问题中都可以利用相同的资料(实际更少--不要求知道标志值具体是多少仅要求知道有多少不同的标志值和它们对应的个数)再计算该广义集合的复杂程度。这启示我们也可以把复杂程度计算用到很多领域去。 | |
| 总体的复杂程度≥部分的复杂程度的合计值。 | |
我们总是可以从某种角度(侧面、层次)把客观事物看成是广义集合,每个广义集合又都对应着唯一的一个复杂程度。于是我们又认识到复杂程度也像质量或者能量那样普遍存在于一切事物中。它提示我们复杂程度和质量、能量都是一样的真实一样的重要。 | |
物质的质量联系着质量不灭定律,物质的能量联系着能量不灭定律,复杂程度也与物质的质量或者能量一样有一个客观规律吗?这是下一篇讨论是问题。在本篇的下一章我们还要讨论复杂程度与信息、熵的关系。 |
--附录:数学说明--