第七章复杂程度概念（2000.4）
| §7.1 从平均值到复杂程度 §7.2 对复杂程度公式的初步说明 §7.3 整体的复杂程度≥各部分的和 §7.4 宇宙的父与母 §7.5 连续变量的复杂程度公式 §7.6 讨论和小结 附录 数学说明 |
人们都吃水稻，水稻种植技术的改进就泽惠众生。 人们都使用“复杂”这个词，把它从定性提高到定量就泽惠众多科学学科。 |
“复杂”是小学生都理解的名词其用途非常广，这也就说明了它非常重要。它目前的弱点是没有定量化。科学发展历史说明重要概念的定量化会推进科学规律的发现。本章的任务是让“复杂”从定性概念走向定量化。
本章指出大家熟悉的平均值都是指广义集合的标志值的平均值 。平均值有很多种它们都是对广义集合的某种计算而得到的一个有特定意义的数值。在引入了标志值的函数的平均值的概念后，我们关注标志值一种特殊的函数的平均值，由于它具有描写广义集合内的状态的丰富程度的含义，我们以复杂程度称呼它，以C表示它。
于是我们就从特殊的平均值的角度引入了一个概念：复杂程度。
本章还对复杂程度公式做了初步分析讨论。广义集合的客观存在伴随着分布函数和复杂程度的客观存在。复杂程度既然是个客观的物理量，它必然有一个复杂（程）度定律存在，这是下一篇讨论的问题。
§
7.1从平均值到复杂程度 现在的小学生学习计算平均值，很多计算器也设计了功能键专门计算平均值，这都说明平均值的应用非常广。我们从平均值谈问题有两层含义：7.1.1代数平均值
一个系统（广义集合）内各个个体有不尽相同的标志值时，如果标志值是数量（离散的或者连续的）人们会问它（标志值）的平均大小是多少。代数平均值（也称为算术平均值）就是一种科学的答案。 全班40个学生的平均身高是多少？只要把每个学生的身高值（hi）相加然后再除以全班人数（40）就可以得出平均身高值（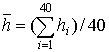
）。写成算式就是
根据这个定义，标志值（变量）xi（i从1，2，到N有N个值）的平均值
的计算公式可以写成
（7.1a）
这里的xi实际是标志值的数值部分，并且把它做数值处理（下同）。N 代表广义集合内个体总个数。N 的值如果不大，用计算器做这种计算并不难。但是N 的值超过50个，计算就难免在输入数据时出差错。克服上述缺点的办法是先求出该广义集合的分布函数再用它计算平均值。例如全校学生有800人，学生身高与人数的关系用分布函数表示如表（7.1）。
表（7.1）不同身高的学生人数和百分比
| 标志值 （身高，m） |
1.25 |
1.35 |
1.45 |
1.55 |
1.65 |
1.75 |
分布函数 |
54 |
78 |
152 |
253 |
169 |
94 |
相对分布函数（ %） |
6.75 |
9.75 |
19.0 |
31.6 |
21.1 |
11.8 |
在表中我们以1.25
表示身高在1.20-1.29 cm范围（余类推）。根据这个表给出的身高与学生人数的关系，平均值
计算公式应当是各档次的身高与学生人数相乘后再相加，最后再以学生总人数去除，即
＝(1.25*54+1.35*78+1.45*152+1.55*253+1.65*169+1.75*94)/800
或 ＝[（身高值）×（人数）]/（总人数）= 1.54
即学生的平均身高为1.54m（米）。以上的求和号Σ代表的不是800个数的相加而仅是六个乘积值的相加。有了分布函数可以大量减少求平均值的计算量。
如果从百分比（相对分布函数）来计算平均值还可以有
＝Σ（身高值）×（人数的百分比）
根据上面的讨论，利用广义集合分布函数求平均值的公式应当是
（7.1b）
这里的k表示不相同的标志值共有k 个。ni 的含义是标志值为xi 的个体的个数。上式的右边求和部分实际上是纯代数的写法（仅利用xi的数值部分）。即平均值就是广义集合多项式的代数值被个体总数N
除。
如果分布函数是以各个标志值在广义集合占的百分比（第三章以p 表示）的形式给出，其平均值的公式更简单：
（7.1d）
这里的a,b分别表示x的下限和上限（本章后面的一些公式中也是以a,b代表下限和上限而不另作说明）。如果用相对密度分布函数（概率密度分布函数）f(x)计算平均值显然应当用下式计算
平均值计算大家比较熟悉。把平均值与分布函数联系起来不仅简化了它的计算，也使表明平均值是对广义集合的分布函数或者代数式的一种特殊的计算。这不仅使平均值找到了主人（广义集合），也丰富了广义集合的形象。
最后要补充的一点，即只有标志值为数值的广义集合才可以计算它的平均值。标志值为字符时无法计算平均值。
7.1.2几何平均值 前面计算的代数平均值在各个部门中用的最广。确实，把各个个体的标志值相加再用个体总量除我们就得到了一个含义非常清楚的物理量----平均值。这个平均值也确实代表了广义集合内标志值的平均水平。但是求平均值并不必须用变量的相加的方法。几何平均值就不是把变量相加，它用的是变量相乘再开方的方法。 与代数平均值公式（7.1a）对应的几何平均值x’公式是
(7.2)
在这里代表从1到N 这N 个x 的值连乘积。把上式取自然对数就有
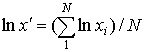
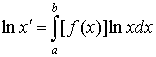
x=3.5
而它的几何平均值x’应当是
这个例子也说明代数平均与几何平均值并不一定相等（一般是代数平均值大）。
从公式中可以看出只要有一个个体的标志量是零，几何平均值就等于零了。另外如果有的个体的标志量为负值还会在开方时出现虚数，从而使计算失去意义。鉴于这些情况几何平均值计算仅能用于每个个体个标志量必然大于零的广义集合（总体）内。而代数平均值就没有这个问题。不过话也可以反着说：只有每个个体的标志值都必然大于零的广义集合才有资格享受几何平均值的优点。 几何平均值对理解复杂程度的概念、后面介绍的幂分布和伽玛（Gamma）分布都有重要意义。 7.1.3标志值的函数的平均值我们讨论了两种平均值的计算方法。不妨说前面求平均值是对广义集合的标志值和分布函数的一种运算。这种运算得到的是一个数而不再是一个函数（这个数的量刚、单位与标志量相同）。现在介绍另一种对标志量和分布函数的运算，它引出来了更广义的平均值概念（它的量纲有可能变化）。
如果把求平均值的公式中的标志值（如x）改为标志值的某个函数[如u(x)]，就得到了标志量的函数u的平均值
。对于标志值的函数的平均值
的公式参照
函数
u(x)的具体形式不同，它可以计算出不同含义的平均值。例如 u(x)=x，它就是代数平均值，如果u(x)=xn 它就是统计学中讲的变量（标志值）x 的n 阶矩。 如果 u(x)=1/x，它的含义就是标志值（变量）的倒数的平均值。习惯上称为调和平均值。如果用x”代表标志值（变量）的调和平均值，计算它的公式就是：
（7.4）
下一篇会用到这个公式。下面介绍另外一种标志值的函数，它引出的平均值就是复杂程度。
7.1.4复杂程度公式 对于一个广义集合，由于其个体总个数N 是确定值，而标志值为x 的个体个数n 是x的函数，所以n/N 也是x 的函数，令
我们就得到了另外一个标志值的函数的平均值，
（7.5）
它就是广义集合的内部状态的复杂程度的计算公式（也是本书中最重要的公式）。公式中的k 表示广义集合内的不同的标志值的个数，ni 表示每种标志值占有的个体的数量，N
是个体总量。
例如有10个不同颜色是球组成一个广义集合。由于每种颜色的球都仅有一个个体，所以上式中各个n的值都等于1，k=10,于是(下面的计算中对数以10为底，而log10=1)
C=-10[log(1/10)]=10log10=10
这就是10个颜色不同的个体组成的广义集合的复杂程度。如果10个球中的颜色都相同，则k=1,n=10,N=10
C=-10log(10/10)=0
即复杂程度是零。比较这两个例子可以看出：
一个系统（广义集合）内的各个个体的特征（标志值）差别越大（如这里的不相同的颜色越多），C值就越大。而各个个体的特征（标志值）完全相同（清一色，没有差别）则C为零。
这说明C值可以综合描述广义集合内各个标志值的差别的严重程度或者说内部状态的丰富程度。有鉴于此，我们称C为广义集合的复杂程度。即（7.5）式就是计算一个广义集合的内部状态的复杂程度的公式。考虑在英文中复杂一词用Complexity 表示，我们用其第一个字母C 表示复杂程度。
或者说，正是由于统计量C具有描述一个系统内的状态的丰富程度的能力，我们才定义它为复杂程度。复杂程度也简称为复杂度。
这样就从特殊的一种平均值的角度引入了一个新的物理量----复杂程度。