钟义信的全信息公式有意义吗?
鲁晨光
1. 引言
大家知道, Shannon信息论只考虑随机信号传递的信息,不考虑语义信息、感觉信息、偶然事件信息。Shannon理论问世不久,当时很有名气的科学家Warren Weaver写了一篇评价和意图推广Shannon理论的文章: “通信数学理论的最近贡献”,和Shannon的文章放一起出版了,书名仍然是Shannon那篇信息论长文的名字:“通信的数学理论”【1】。Weaver在这篇文章力里提出了“通信的三个水平”的著名论点,对后来的学者推广Shannon理论起到很大影响(有关研究参看我的网页”广义信息论溯源”,网址http://survivor99.com/lcg/books/GIT/sy.htm)。
钟义信是北京邮电大学教授、博士生导师、副校长、校学术委员会主席,国家863计划通信主题首届首席专家,中国通信学会通信理论委员会主任委员,….(更多头衔参看:http://www.bupt.edu.cn/~icii/president/zhong.htm)。他最为著名的研究成果是他的全信息理论【2】――该理论试图贯彻Weaver的通信的三个水平思想。
我也是一个广义信息论研究者【3】,因为出过专著《广义信息论》【4】,不少人要我谈谈我对钟义信全信息理论的看法。我过去一直没把这当回事。我以为,就信息论来说,钟义信的最大贡献是使Weaver的广义信息论思想在中国广为传播, 而他自己建立的全信息理论并没有多少实质性进展;特别是,他提出的那些全信息公式,完全经不起推敲,不会有人拿它们当真。但是最近, 我发现,许多年轻人把钟义信的全信息理论当作权威理论,很少怀疑。现在我觉得,如果明知其错误而不作澄清,那将误国误民!
因为在学术刊物发表批评文章太难(比如按《电子学报》的做法,文章要征求被批评人意见,这一关就很难过),所以我将文章贴在网上。
科学理论是可以检验的,一种信息理论或一个信息公式是否合理, 我们用它解释和验算日常信息交流实例就知道了。钟义信的公式是否经得起检验呢?十多年前,钟义信用加权系数或开关函数把Shannoon熵,模糊熵等加在一起,说那说全信息熵。我说模糊性只能减少信息,不能增加信息(后来我发现,在预测不准时, 模糊性可以减少负信息的绝对值,是一种保守策略),相加是没有道理的。他说:全信息熵不是信息, 先验熵减后验熵才是信息。我仍然存有疑问。我问他是否能用他的公式度量任何一种广义信息――比如天气预报信息,经济预测信息,颜色视觉信息….。钟义信的答复是:他现在的研究还处在理论探讨阶段,还没有用到实践。十多年过去了,钟义信的公式,以及这些公式的应用和检验有所进展吗? 几乎没有!其理论建构得更庞大了,传播更广了,可是内核还是那些不能解释任何信息交流的全信息公式。
其实拿日常信息交流事实来检验信息理论也不是什么难事。 钟义信自己不愿检验,我来帮他检验。感谢互联网,让大家都可以发言,都可以反驳别人。我相信白纸黑字, 是对是错, 大家迟早能分得清。下面我从日常信息交流实例来看钟义信的全信息公式的荒谬性。要是钟义信和任何其他人嫌我举的例子不典型, 他可以拿出更典型的例子来。 同时我也愿拿我的信息公式来供他或别人检验(参看下面附录或网页:http://survivor99.com/lcg/books/GIT/index.htm)。
2. 钟义信的全信息公式
要知道钟义信的全信息理论的来源, 我们先看看Weaver关于通信三个水平的论述【5】:
Level A. How accurately can the symbols of communication be transmitted? (The technical problem.)
Level B. How precisely do the transmitted symbols convey the desired meaning? (The semantic problem.)
Level C. How effectively does the received meaning affect conduct in the desired way? (The effectiveness problem.)
There is a close relation between these levels and the semiotic distinctions:
A: Syntax and the forms of language.
B: Semantics and the meanings of language.
B: Pragmatics and the use or function of language.
要知道钟义信全信息公式的来源,我们还要看Deluca-Termini的模糊测度公式:
F(A)= -∑ [mi log mi + (1-mi) log(1-mi)]/N (∑是求和,i从1到N) (1)
其中A表示模糊集合,F表示模糊度, mi表示xi在A上的隶属度。这个公式本来是用来度量模糊集合的模糊度的。 可以证明:对于所有i, mi=0.5时, 模糊度最大,等于1。说明这时集合A最模糊。当所有mi=0或1时, 模糊度最小,等于0。这说明集合是清晰的。作为模糊度,上面公式是合理的。
现在我们看钟义信的全信息公式:

图1. 钟义信的全信息公式【6】
其中, 随机(random)信息就是Shannon信息。 偶然(Incidental)事件信息比如:上课铃或地震警报提供的信息。 模糊(Fuzzy)信息比如模糊语句”明天可能有雨”提供的信息, cn就是模糊数学中某元素在某模糊集合上隶属度, 我后面用mi表示。 上面语义信息公式中tn是命题的可信度。 xi在模糊集合A上的隶属度mi,就是命题“xi在A中”的可信度, 所以后面我同样用mi表示。 在我看来,只有语义信息,没有语法信息。如果说有语法信息, 那只是语义信息在预言或命题总是正确时的特例。其中un代表效用. 应该在0和1之间变化.
钟义信的语义信息I(T;X)和模糊度F(A)之间的关系是:
I(T; X)=最大可能模糊熵-模糊熵=log2-F(A)
(2)
其中log2是最大可能信息。后面我们重点讨论钟义信的语义信息公式。其他公式的荒谬是类似的。
3. 通过计算看钟义信语义信息公式的荒谬
钟义信的语义信息大小可用图三说明。
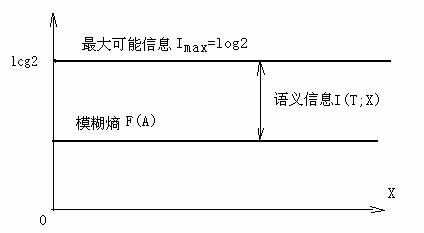
图3 钟义信的语义信息图解(语义信息和事实X=?无关)
我们用天气预报来说明集合和语言的模糊度和信息计算。
设U是不同降水量集合,xi是U中元素, A是U上的一个模糊集合{有小雨},mi是降水量xi在A上的隶属度,或命题“xi在A中”的可信度,那么F(A)就反映A的模糊度。假设有4个语句: y1=”明天肯定无雨”; y2=”明天阴有小雨”; y3=”不确定明天有雨还是无雨”, y4=”明天可能有雨也可能无雨”. 响应的模糊集合是 A1={无雨}, A2={有小雨}, A3={不确定有雨还是无雨},A4={有雨或无雨}。 那么这四个集合的隶属函数及响应的语义信息I(T; X)可用下图表示:
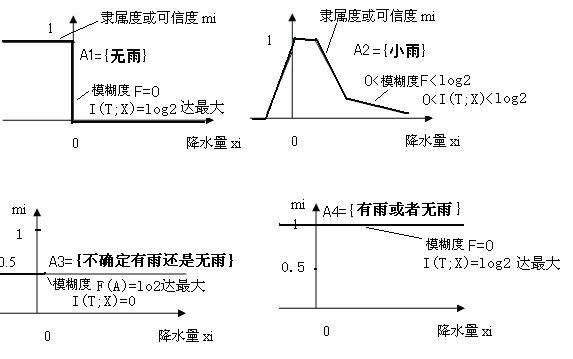
图2 模糊集合隶属度及模糊测度
那么这四个语句或集合的模糊度如何呢? 计算可知: F(A1)=F(A4)=0, F(A2)大概是0.2-0.4比特, F(A3)=1比特达最大。这符合我们通常的”模糊”概念。 有人可能认为第四个语句是模糊度的,这是不对的。 因为y4=”明天有雨或无雨”在任何情况下都是对的, 可信度总是等于1,所以其模糊度等于0。
如此计算出的语义信息存在这样一些问题:
1) 信息量大小和哪一个xi实际发生无关。如果明天下雨,你预报“无雨”,预报错了,信息量也是这么多吗?按照常识,预测错了, 信息量是负的才对。可是钟义信采用的公式太简陋了, 根本无法顾及预言对错问题。没有对错检验, 如何度量语义信息?
2) 语句y4=”明天可能有雨也可能无雨”和y3一样,是废话,不提供任何信息。可是按钟义信的公式,y4提供的信息达最大。这不符合常理。
3) 按照常识或Popper的科学进步理论, 把一个越是偶然或特殊的事件预测对了,信息就越多。比如“明天有特大暴雨”提供的信息就比“明天有雨“提供的信息多,如果两者都是对的。而按公式(2), “明天有雨”提供的信息可能还多些, 因为它更加不模糊。这是违背常识的。
4) 按公式(2),语义信息最大量是log2=1比特。这是不合理的。我们用Hartley公式粗略地计算, “特大暴雨”的信息I=log(总天数/特大暴雨天数)也不止2比特。一个好的广义信息公式应该和经典信息公式兼容,这在钟义信那里完全做不到。
5) 我要问:按图1或公式(2)算出的信息I(T;X)是一个语句y(比如“明天有雨”)和它的否定语句not y(“明天无雨”)提供的平均信息,还是单个y提供的信息? 如果是平均信息, 应该有两者出现的概率才是(现实中等概率情况是没有的)。如果是单个语句信息,通过计算我们会发现, y和not y 提供的信息一样多。事实怎么会有这种情况呢? 把有雨说成“有雨”和把有雨说成”无雨”,语义信息是一样的吗?
6) 语言信息交流时, 可选择语句一般来说有许多,比如天气预报语句有:“有小雨”, “小到中雨”,“中到大雨”….这时候如何用Deluca-Termini公式?该公式用到A和非A两个集合隶属度,是因为两者是互补集合。语句多时,考虑互补集合,问题就复杂了,采用DeLuca-Termini公式显然不行。
上面的例子中,我们把天气预报换成粮食产量预测,股市指数预测,问题是一样的。如实描述事实的语句是预言和事实符合情况下的特例,问题2)-6)依然存在。这些都说明, 用模糊度或模糊度的差根本就不能解决语义信息度量问题!钟义信用它们只能得到荒谬结果!
4.如何理解语用信息?
效用在经济学中是非常基本的概念, 但是也是没有明确定义的概念。 我们可以用获得的财富价值作为效用, 也可以用价值的对数作为效用. 甚至也可以用达到目的的程度作为效用。 钟义信用的就是后一种, 因为其最大值是1.
首先,其通信模型含混不清。 我不禁要问: 究竟什么提供关于什么的信息? 是关于效用的语言或预言提供信息, 还是实现效用的进度ui提供信息?
为什么效用函数可以放到对数后面, 而且这样就表示信息? 无论是Shannon公式还是Deluca-Termini公式, 对数里面放的都是不确定性测度。 概率测度pi是客观事件的随机不确定性测度, mi是主观概念外延的不确定测度[6]。 而效用和价值概念完全不同,他们不是不确定测度。
我觉得, 钟义信对Weaver效用信息的理解很成问题。 在我看来,只有服务于效用或围绕效用而优化的语义信息,并没有用效用计算出的所谓的效用信息,或者说,用效用的对数计算出的东西不是信息。按照钟义信的做法, 好像我们计算什么信息就要把什么量放到信息公式中去。 我们计算能源信息,是否就应把能量数值放到公式中去,计算温度表信息就要把温度数值放到公式中去?
虽然,我也有类似做法,我在《投资组合的熵理论和信息价值》里把资本价值(未必小于1 )放进某种熵公式里了, 但是我用来表示的不是信息,而是资本增值速度, 表示多少轮投资后,平均翻多少倍,意义很明确。钟义信的语用信息I(U;X)究竟表示什么?
我们还是用天气预报来检验他的公式。假设,某林场希望在最近一次下雨前后栽树, 所以对下雨的时间要掌握准确。差错时间越长,损失就越大。我们假设效用函数是
ui=1-f(xi-x0) (3)
其中x0是实际下雨时间, xi是预测下雨时间。1是准确预测时的效用值,f(xi-x0)是|xi-x0|的单调增加函数, f(xi-x0)最大值是1 。ui就是钟义信效用公式中的un. 按照上面效用信息公式, ui=1,2,…n, 确定了, 语用信息I(U;X)就确定了, 和预测完全无关? 不管你预测哪天下雨, 结果都一样。这叫什么效用信息?
即使只带入实际预测的时间xj一个值进公式,算出uj, 别的ui不要了,或者让别的ui都等于uj, 结论也奇怪:不是预测最准的时候(xj=x0),信息量最大,而是效用函数uj=0.5时信息量最大。这样的语用信息有意义吗?
我记得在纪念Shannon信息论诞生50年的宜昌信息论会议上,北邮的吴伟陵老师的报告非常精彩,他说Shannon信息论的核心是他的通信优化思想。 我以为Weaver提出语用信息也是从优化的角度来讲的。研究语用信息的目的是要:如何用尽可能少的信息(Shannon信息或语义信息)得到尽可能多的效用,或信息价值。我很难相信钟义信对Weaver思想的理解符合其原意。
5.结束语
以前的说法不妥, 现在纠正--2016-2-19.
现在我相信钟义信作为信息科学旗手不比英国的Floridi差。 他的公式是有问题, 看来和整个学术风气有关。 我们缺少相互交流,相互批评, 共同研究的学术气氛。相互批评的文章也不容易发表、
注释:
【1】The Mathematical Theory of Communication, Claude E. Shannon and Warren Weaver, The University of Illinois Press, 1963
【2】参看钟义信的专著:
《信息学漫谈》,中国科学技术出版社,1884
《信息科学基础》,和平出版社,1984
《信息的科学》,光明日报出版社,1986
《信息科学原理》,福建出版社,1988
《信息技术导论》,上海科学技术出版社,1994
《信息科学原理》北京邮电大学出版社(再版),1996
钟义信主页介绍说:(他)具有重要创新意义的学术贡献主要包括 “知识论”、“全信息理论”、“意识机模型”、“信息科学原理与信息科学方法论”、“信息基础结构理论模型”等。 其中《信息科学发展研究》和《信息科学原理》被评价为“开创性著作”,“由信息论到信息科学的标志”,分别获得邮电部科学进步一等奖和二等奖, "基于全信息理论的智能型自动文摘系统" 等多项研究成果通过专家鉴定,评价为国际先进水平。
【3】我的个人主页: http://survivor99.com/lcg
【4】鲁晨光,《广义信息论》,1993,中国科学技术大学出版社。
【5】来自网页:http://coral.lili.uni-bielefeld.de/Classes/Winter98/LingHyper/Hyptext/Text/hyptext/node8.html
【6】参看:自然语言理解与全信息理论――方法论的探讨及应用,网址:http://www.china-language.gov.cn/doc/NLP0/06.pps