From Hartley’s Information Formula to Generalizad Information Formulae
—Explaining Intuitively with fish-cover model
Lu/Chenguang (independent researcher)
Abstract: With the fish-cover model, the paper intuitively expains the measurement of information by extending Hartley formula to generalized information formula gradually. It also discusses the essence of information and how to set up the bridge between classical information theory and scientific evolution theory.
Keywords: formulae of information amount, measuring information, sensitive information, semantic information, essence of information.
从Hartley信息公式到广义信息公式
――用罩鱼模型通俗讲解
鲁晨光 (独立研究者)
230063 安徽省合肥市省出版局鲁茂松转
摘要:本文通过罩鱼模型,直观地说明信息的度量――从简单的Hartley公式,一步一步推广,得到广义信息公式。并由此说明信息本质, 以及如何在经典信息论和科学知识进化论之间搭起桥梁。
关键词:信息量公式,测量信息,感觉信息,语义信息,信息本质
在日常信息交流和电子通信之间, 在哲学信息研究和电子信息研究之间(比如在Popper 和Shannon之间)存在巨大鸿沟。我的努力是在两者之间搭起桥梁。我以为我找到了所需要的工具,搭起了如愿的桥梁(参看笔者的《广义信息论》[1])。这里我用尽可能易于理解的语言,叙述如何逐步推广经典信息公式得到广义信息公式。我希望我的努力有助于大家对信息本质的理解。
1 Hartley信息公式和简化通信的鱼罩子模型
Hartley信息公式【2】是
I=logN
(1)
其中I表示确定N个等概率事件中的一个出现时提供的信息。如果事件y把不确定范围从N1个缩小为N2个,那么信息就等于
I=I1-I2=logN1-logN2=log(N1/N2)
(2)
我们且称这个公式是Hartely信息差公式。在说明这个公式性质之前,我讲一个用罩鱼子捕鱼的故事。
鱼罩子是用篾做的,像过去家家户户用的烤火罩,形如半球壳,上面有个圆口,便于抓鱼。它适合浅水捕鱼。我小时候看人家用鱼罩子捕鱼,我也拿个通了底的篮子学着捕。也真捕到了。后来我总结经验:鱼罩子大,容易罩住鱼,但是罩住以后抓鱼困难些。如果鱼罩子和池塘一样大,那就百发百中,但是没有意义,因为要抓到鱼,还是一样很难。我用篮子或小鱼罩子罩鱼,虽然罩中困难,但是罩到了,抓就很容易。
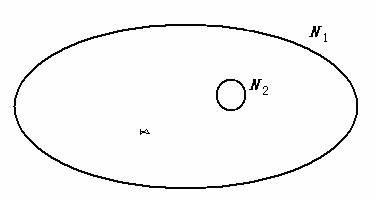
图1 信息的罩鱼模型
一个不确定事件就像是池塘里随机出现的一条鱼,设事件y=罩住鱼了,y就提供关于鱼的位置信息。信息是多少呢?如N1是池塘的面积,N2是鱼罩子底面积, 那么信息就是I=log( N1/ N2)。N2相对N1越小,信息量越大,这正反映了篮子的优点。当N2= N1时,信息是0, 这正反映:鱼罩子和池塘一样大,罩中也没有意义。至于鱼罩子和篮子相比的优点,上面公式不能反映,因为使用Hartlry公式有这样的前提:客观事件必然是N2个事件中的一个。相当于假设:鱼罩子或篮子不会罩不中鱼。后面我们将通过广义信息差公式解决这一问题。
我们称上面罩鱼假设为通信的罩鱼模型。相应的信息公式是Hartley信息差公式。
3 模型改进――把物理空间或事件空间变为可能性空间
用Hartley公式计算信息,N个事件是等概率的,但是通常的情况并不如此。 比如,鱼在水深的地方可能性大些,在水浅的地方可能性小些。这时候如何处理? 这时候我们用可能性空间大小代替池塘面积就行了。
我们用1表示可能性空间大小,那么池塘面积N1就变成1, 鱼罩子面积N2就变成P= N2/ N1。公式就变成【5】
I=log(1/P)
(3)
4.相对信息公式
我们再假设:池塘可化成若干块,鱼在某一块的概率是P1, 正确判定鱼在某一块(判断y0)的信息是I 1=log(1/ P1)。用鱼罩子罩住鱼,或者确定鱼的位置(判断y)提供的信息就是I2=log(1/ P2)。我们把已知y0时,y提供的信息称为相对信息, 那么相对信息量是:
I=I2- I1=log(P1/ P2)
(4)
我们设鱼所在位置为随机变量X, 它取值于集合A中元素, A={x1, x2, …}; 随机事件Y提供关于X的信息, Y取值于B中元素,B={y1, y2,…}。那么相对信息公式就是
![]()
(5)
其中I(xi; yj)表示yj 提供关于xi 的信息, P(xi )是鱼在位置xi 的概率,P(xi | yj )是给定yj 的条件概率。
值得特别注意的是,这个公式要求y0和y1 都是对的, 如果有一个不对,公式都不能成立。 Shannon从来不谈单个事件的信息,只谈事件的平均信息,就是因为单个事件信息涉及到判定准确与否问题。而Shannon避免谈论语义问题。
5.Shannon互信息公式和Kullback信息公式
我们用求数学期望的办法可以求出yj 提供的关于X的平均信息I(X; yj ):
![]()
(6)
该式也就是Kullback信息,可用来计算单个事件提供的平均信息。再用类似的方法求不同Y关于X的平均信息, 于是得到Shannon互信息公式【3】:

(7)
其中H(X)是X的熵, H(X|Y)是X的条件熵。当Y=X或者H(X|Y)=0时(Y和X有确定对应关系时),Shannon互信息就等于Shannon熵。即
I(X;Y)=H(X)
(8)
而这在一般情况下熵不成立的。一般情况下H(X)不表示X的平均信息,它表示潜在的最大可能信息。
6.用相对信息公式度量测量信息
现在我们以温度表信息为例,说明如何用相对信息公式度量信息。
如果假设实际温度是X, 读数是Y; A={x1, x2, …},B={y1, y2,…}, 读数是Y= yj 时,最大可能的温度是xj 。假设“鱼罩子”清晰,当读数是yj 是, 实际的温度一定在某个确定范围Aj内, 比如Aj =[xj-0.2, xj+0.2], 当xi发生时, 我们就用上面的相对信息公式计算信息:
![]()
(9)
其中P(xi| Aj)是已知xi在 Aj中,xi发生的概率。
设集合Aj的特征函数是Q(Aj|xi)(呈矩形), 根据Bayes公式, 有
P(xi |Aj)=Q(Aj | xi )P(xi )/Q(Aj )
(10)
其中Q(Aj)是Q(Aj | xi )的平均值。即
![]()
(11)
由(9)和(10),我们得到
![]()
(12)

图2 测量信息图解
我们称该信息公式是集合信息公式。因为它度量的是:事件“X在集合Aj”中提供的信息。这个公式要求实际发生xi必然在Aj中,如果不在,信息是负无穷大。没有意义。
7.混淆范围模糊时的测量信息
上面我们假定,读数是yj时,X必然在Aj中,并且Aj是清晰集合。特征函数Q(Aj|xi)可理解为xi和xj相混淆的概率。对于清晰集合Aj,如果xi在Aj中,混淆概率时1, 否则是0。而实际情况是,Aj可能是模糊的,混淆概率可能在0和1之间变化。
假设我们做许多次试验,当读数Y= yj时,改变xi, 只有当xi和xj差异大到一定程度,读数才会变化。 不引起读数变化的所有xi构成的集合是一个清晰集合,许多次(设为n->无穷大)试验得到许多这样的集合sj1, sj2,…sjn,然后我们定义
![]()
(13)
是xi和xj 相混淆的混淆概率, 它也就是xi在模糊集合Aj 上的隶属度【4】。其中Q(sjk|xi)表示集合sjk的特征函数,也就是第k次试验得到xi和xj的混淆概率(等于0或1)。
混淆概率函数曲线Q(Aj|xi)形状类似于正态分布函数。
要计算混淆范围模糊时的温度信息, 我们只需要用混淆概率函数取代前面的特征函数,公式如同(9)和(12),是:
![]()
(14)
这就是广义信息量公式。不同的是,这里Q(Aj|xi)是山形函数而不是矩形函数。
公式(14)的几何性质如图3所示。它表示,当读数是yj时, 实际发生的xi 与xjj差别越大,信息量越小。差别大到一定程度,信息量就是负的。如果把Q(Aj|xi)理解为命题yj为真的可信度函数,这个公式就可以用于语义和预言信息计算(参看图3)。
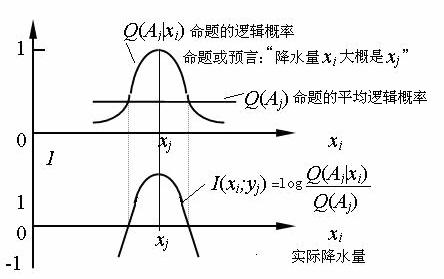
图3 广义信息量(测量信息和预言信息)公式图解
这个公式在测量不准时(比如由于误操作),算出的信息量也是合理的。负信息表示错误的测量结果和谎言会减少我们已有的信息。
根据这个公式,越是把偶然的东西预测为必然,并且预测正确,信息量就越大,反之就小。谎言提供的信息是负的。如果把这样的信息作为评价科学理论的标准,则命题或预言的先验逻辑概率越小,后验逻辑概率越大,相应的理论就越有价值;若两者总是相等,理论就是非科学的。这和Popper的结论是一致的。
8. 预言信息度量
像“降水量大概是x毫米”,“下一此地震的地理位置大概是经度x纬度y”之类的带有数字的预测, 显然可以用上面广义信息公式度量。 对于一般的语义信息,比如“明天有小雨”,或“明天有小到中雨”,公式同样适用。这时候Q(Aj|xi)表示xi 在模糊集合Aj上的隶属度。它同样可以假设为随机集合的统计结果【4】 我们也可以这样理解:相对命题yj , 存在一个理想事件xj(相当于柏拉图的理念,不一定在Aj中),任意xi 在Aj 上的隶属度就是xi 和理念xj混淆的概率。这样测量信息和语义信息在本质上就没有什么不同。
我们还可以把Q(Aj|xi)解释为命题“xi 在Aj中”的逻辑概率。理念xj在Aj 中的逻辑概率是1, 其他xi 在Aj 中的逻辑概率小于或等于1。而Q(Aj)就是谓词yj(X)的逻辑概率, 或命题yj的先验逻辑概率, 和平均逻辑概率。所以, 语义信息量

(15)
这一语义信息公式能够反映Popper的科学知识进化思想。它表明,越是把原以为偶然的事件预测准了,信息量越大;命题的先验逻辑概率越小,后验逻辑概率越大,信息量越大;语言模糊将减少信息的绝对值――因为说错了,负的信息量很大;永真命题信息是0 [2]。
假设总有Q(xi|Aj)= P(xi|yj), 语言信息就变为描述事实的语义信息。所以,语言描述信息是预言信息的特例。
9.广义Kullback公式和广义互信息公式
我们对广义信息I(xi; yj)求平均, 就得到广义Kullback公式
![]()
(16)
其中P(xi)也可以不是来自统计,而是来自主观估计,这时候我们记它为Q(xi)。广义Kullback信息公式的性质可以通过图4说明。可以证明,当预测Q(X|Aj)和事实P(X|yj)越是重合,信息量越大, 信源P(X)或先验估计Q(X)越是与事实P(X|yj)不同(表示预测的事情越是出乎意外),信息量越大。这和公式(14)一样,体现了Popper的科学进步评价准则。不同的是, 这里所预测的事实不是简单事件,而是时间或空间种分布的事件。
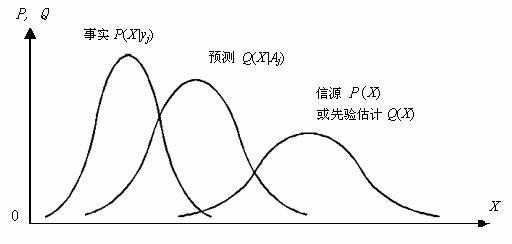
图4 广义Kullback公式性质――反映Popper科学进步评价准则
再对I(X; yj)求平均,我们得到广义互信息公式
I(X;Y)=H(X)-H( X|Y)=H( Y)-H( Y|X)
其中
![]()
(16)
是广义熵,
![]()
(17)
是广义条件熵或模糊熵。可以证明Deluca-Termini模糊熵【5】是上面模糊熵的特例。
9.从色觉、编码、数字图像、海啸预测和设计图纸的信息度量看信息的本质
我之所以举这5个例子,是因为他们很有代表性。如果这几种信息度量问题解决了,其他信息度量也不成问题。
1)色觉信息
色觉信息和温度表读数信息是类似的,不同的是:对于每种温度读数yj ,真地存在一个xj。但是对于色觉来说,相对一种色觉yj,并不存在一种色光,而是存在许多色光――同色异谱色光。但是这时候我们不妨任选其中一种作为xj, 然后通过试验得到混淆概率函数Q(Aj|xi), 由该函数和P(xi)算出Q(Aj), 从而用广义信息量公式算出感觉yj的信息I(xi; yj)。
2)编码信息
常见的编码有ASCII码,莫斯电码,相对某个文件的特殊编码。古人结绳记事也是一种编码。编码一是为了适合信号传递,二是为了节省信号数量。
假如有一组码{x1, x2, …}, xi出现的概率是Pi, 那么编码的平均信息就是Shannon熵H(X)。log(1/Pi)就是xi出现提供的信息。Shannon理论表明,如果信息量小的字母,比如e, 码长较短,信息量大的字母,比如z, 码长较长,那么,传递文件的平均码长就能较短,并接近仙农熵。这就是为什么莫斯码长短不一。
假如有一组码{y1, y2, …}编码允许误差,给定误差限制集合,比如用为yj 编的码一定在Aj中,Aj 是模糊的或清晰的, 那么,根据Kolmogorov的复杂性理论【6】,我们可以用最短码长定义编码信息。我在《广义信息论》第五章定义的限误差信息率就是这一信息,我证明了,它就等于式(16)所示广义熵。
3)数字图像信息
一幅M行N列的彩色图像可以设想为 3×M×N维矢量空间中的一点, 点是简单的, 但是可能性空间变大了。知道该点发生的先验概率P,就能计算其信息I=log(1/P)。
从我的广义信息论看, 3×M×N维矢量空间中的一点和它相邻的许多点是不可区分的, 信息多少和人眼分辨能力有关。计算信息要用广义信息公式(13)。
Kolmogorov的复杂性理论[3]应该说是仙农理论的一个很好补充。该理论假设我们不知道信源的性质—概率分布P(X), 只知道信宿—比如一幅数字图像(或一串0-1码)—是什么样子。 把数字图像压缩编码, 无失真编码的最短码长就是图像的复杂性, 也就图像的信息。 用这种观点理解图像信息, DNA遗传信息….似乎比用仙农理论更直观。
假设有M行N列彩色图像, 每一点用颜色矢量(b,g,r)表示,颜色空间有256×256×256格点。这样定义图像信息实际上是假设先验熵达最大,为Hm =3MNlog(256)=24MN (bits)。因为图像有规律(比如工程图纸),比如相邻象素的颜色之间有相关性,而规律提供信息Ir,利用这些信息为图像编码就可以减少码长。图像的复杂性或信息就是Ic=Hm-Ir。按照这种定义,无规则的图像最复杂,信息量最大。
但是, 我们要注意,这样的信息和仙农信息是不同的,仙农理论或广义信息理论度量的是图像反映外物(各种可能外物中的一个)的信息,而Ic反映的是:要为图像无失真编码, 需要多少信息。
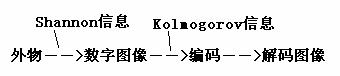
图4 Shannon信息和Kolmogorov信息的区别
而编码信息可以用仙农熵度量。码的长度越长,码所表示就是维数更多空间中的一点,不确定空间就越大,码就越特殊,信息就越多。所以,Kolmogorov信息,或用复杂性定义的信息,并不超出仙农理论。
4)海啸信息
海啸预测和前面说的降水量预报是类似的。只是可能性空间复杂一些。一个可能的预测yj 是:海啸发生时间大概是某天――设为dj,引起海啸的地震中心大概是某处—设为经度aj, 纬度bj 附近,严重程度是cj。设此四维空间化成许多小块,地震发生在点(dj, aj, bj, cj)所在的小块的概率是P(dj, aj, bj, cj) 。 逻辑概率Q(Aj|xi)可以假设为以时空坐标xj=(dj, aj, bj, cj) 为中心的正态分布函数,它就像一个边界不太清晰的大鱼罩子。这样就可以算出实际发生xi=(di, ai, bi, ci)时yj 提供的信息I(xi; yj)。可以证明,对于越是偶然发生的大海啸,预测的逻辑概率函数Q(Aj|xi)覆盖的海啸范围越是接近受灾范围,信息量就越大。反之,信息越小,甚至是负的。这是符合常理的。
5)设计图纸信息
图像信息是衡量主观感觉和认识同客观事物符合与否的信息, 而设计图纸信息是衡量客观事物和主观设计符合与否的信息,两者都存在符合不符合问题,以及所反映的东西是否特殊问题。
如果有某人的某项设计yj, 各种不同建筑出现的概率分布是P(xi), i=1,2,… 一种建筑xj和其他建筑xi的混淆概率是Q(Aj| xi), 那么我们就可以用(12)和(13)计算设计图纸信息。如果建成的建筑和设计完全一致,那么信息就变为I(xj; yj)=log[1/Q(Aj)]。可见,设计图纸信息和其创新有关。但是如果设计有问题, 无法施工,甚至不久倒塌, 那么信息就是负的。
如果计算设计图本身的复杂性或信息,那么它就是绘出图纸的最简程序(用0-1码编写的)长度。仍然反映的是某种特殊性。
从上述例子看,说”信息是被反映的特殊性” 仍然成立。从各种信息的度量看,信息的本质仍然如罩鱼模型(鱼罩子可能是模糊的)所示,是减少的不确定性;或者说:是被反映的特殊性(关于信息论的更多讨论参看我的个人网站[4])。
[1]鲁晨光,广义信息论,中国科学技术大学出版社,1993
[2] Hartley R V L. Transmission of information, Bell System Technical Journal,7 (1928),535
[3]Shannon C E. A mathematical theory of communication,Bell System Technical Journal,27 (1948),379—429,623—656
[4]汪培庄. 模糊集和随机集落影,北京师范大学出版社,1984.
[5] De Luca A. and Termini,S.: A definition of nonprobabilistic entropy in the setting of fuzzy sets,Infor. Contr. 20(1972),201—312
[6] Ming Li and Paul Vitanyi, An Introduction to Kolmogorov Complexity and Its Applications, Springer-Verlag, New York, 1993; Revised and Expanded Second Edition 1997
(2005-5-12修改稿)