语义信息公式浅谈及图解
鲁晨光
1.经典信息量计算公式
仙农没有提供单个信号信息量公式,只提出平均信息量公式:
I(X;Y)=H(X)-H(X|Y)
(1)
意思是:随机信号Y提供关于随机事件X的信息等于X的先验熵H(X)减去X的后验熵H(X|Y). 有时候我们也说H(X)是平均信息量,那是假定,Y=X,这时H(X|X)=0. 于是I(X;Y)=H(X).
倒是Hartley曾提出了单个事件的信息公式:
I=logN
(2)
比如掷骰子打赌,一个骰子显示的数目是6个当中的一个, 于是信息量等于log6=2.59比特(以2为底). 后来有人结合Hartley公式和Shannon公式, 提出用
I=P2/P1
(3)
计算单个事件的信息。其中P2表示后验概率, P1表示先验概率。比如100个人摸奖,最后只有一人得奖. 假设事件y=前面90个人没摸到,那么,开始模奖时,以=每个人得奖的概率P1=1/100, y发生后,剩下10个人,每个人得奖的概率P2=1/10, 那么y提供的关于剩下10个人中谁得奖的信息就是I=log(P2/P1)=log(10)=3.32比特.
显然, 这个公式和Hartley公式是相通的。可以证明,它和Shannon公式也是相通的。
2. 单个语句信息量计算
2.1 两个困难:符合-不符合问题和精确-模糊问题
语义信息计算有两个困难。 一是有对错检验问题,也就是语义和客观事实是否符合问题;二是如何处理好语言的精确性和模糊性问题。好的信息公式要保证:1)说对了信息(量)就多, 说错了信息就少, 甚至是负的; 2)越是精确信息量绝对值越大(如果是错的,负信息量也越大), 越模糊信息量绝对值越小。
因为正确描述语句是预测或预言在预测符合事实时的特例,所以我们只考虑一般情况的语义信息――预言信息。
假设我们预测最近一个月降水量X,如果你预测是:”降水量大概是10毫米”,而结果是0, 5,10, 15 ,20…毫米, 那么,好的信息公式应当有怎样的结果呢?对于该具体问题,公式
I=m-|X-10|
(4)
计算出的结果比较符合常识。参看图1。据此,预测误差越大,信息越少,甚至是负的。事实最符合预测时信息量最大, 为m。
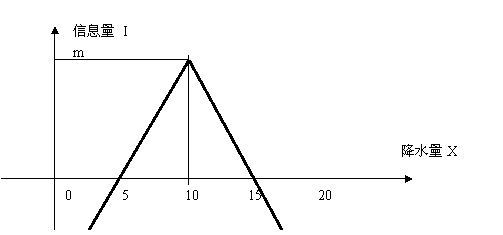
图1 一个特殊情况下的符合常识的信息量计算图解
但是,要度量这样的模糊语句“降水量不小于10毫米” 的信息量,这个公式就不行了。要区别模糊语言和不模糊语言的信息量,比如区别“有中到大雨”和“可能有雨”的信息量,这个公式更加不行。
2.3 新的语义信息计算公式及其和Popper科学进化理论的一致性
能不能找到更好的信息量计算公式呢? 有,我找到了, 其实很简单:
信息量I=log[命题的逻辑概率/谓词的逻辑概率]=log[Q(Aj|xi)/Q(Aj)]
(5)
其中xi是客观事件,Aj事件的模糊集合;其中Q(Aj|xi)是命题yj=“xi在Aj中”的逻辑概率。用不确定的X代替确定的xi, 命题yj(xi)就变成谓词yj(∙)。 Q(Aj)是谓词yj(∙)的逻辑概率,它是命题的逻辑概率Q(Aj|xi)的平均数:
Q(Aj)=∑ P(xi)Q(Aj|xi)
(6)
命题的逻辑概率Q(Aj|xi)就是也就是学者们常说的命题的可信度。它就是事件xi在模糊集合Aj中的隶属度。因为我们用可通过语义试验的统计得到该隶属度和可信度(参看附录1),所以我用“逻辑概率”而不用“可信度”。
用公式(5)是否会得到和公式(3)类似的结果呢? 可以!图2 计算结果显示,所计算出的信息同样能保证:预测误差越大,信息量越小,甚至是负的。事实最符合预测时,即降水量就是10毫米时,信息量最大。
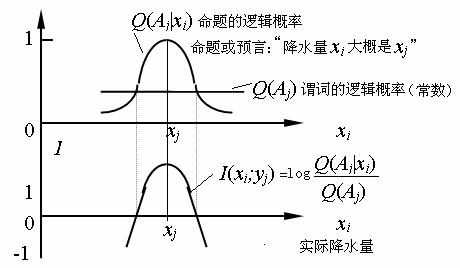
图2 单个语句信息量计算图解
这个公式不仅能反映预测误差减少信息,还包含了哲学家Popper的知识进化评价准则(包括模糊性减少信息)。
图3显示的是股市指数预测信息评价,我们也可以把它当作降水量预测信息评价,海啸死亡人数的预测信息评价,石油产量和价格预测信息评价。其中Q(X)表示的是未来不同指数发生的先验概率估计。当前指数是x0, Q(X)往右减小表示先验估计的更大指数发生概率渐小。山型曲线表示命题的逻辑概率。

图3 语言模糊性不同、被预测的事件偶然性不同时的预测信息比较
该图表明:1)语言越精确,信息量的绝对值越大,但是因预测错误而减少信息的可能性也越大;语言越模糊,信息的绝对值越小,因犯错误减少信息的可能性也越小; 2)越是把源以为偶然的信息预测对了,信息量越大,反之信息量越小。这正反映了Popper的科学进化信息准则[1]。
假设有预言:“股市指数可能涨,也可能跌”, “明天可能有雨也可能无雨”,这时命题的逻辑概率总Q(Aj|xi)总是最大,为1;谓词的逻辑概率也必然是1,所以可以算出信息总是0。这正反映了Popper名言:永真命题不提供任何信息,不是科学命题,因为不可证伪。
(未完待续)