分布函数b

§3.3 例子

分布函数定量说明了广义集合的内部结构。

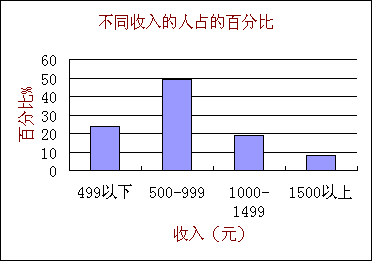
个人收入是个重要问题。我们也可以把它归为一个广义集合（个人是“个体”，收入是“标志值”）把个人收入问题提为“不同的收入的个人各有多少”问题。而它的答案是一个分布函数。国家统计局对我国12个城市的调查结果（引自1998年12月《百科知识》26页，估计是1997年的资料）是表3.2

表3.2 不同的个人收入各有多少的一个调查结果（12个城市）

标志值x ：每人每月收入（元）	499以下	500-999	1000-1499	1500以上
个体数量n（相对）：占的百分比	24%	49%	19%	8%

图表对象不同收入的人占的百分比

很显然这个统计恰好符合分布函数的格式。它描述了一种经济结构。

发现水的化学成分是氢二氧一在化学上是重要的事，如果把一个水分子看成是一个广义集合，并且把原子看成是个体，那么水的化学成分的发现也就是在原子水平上认识水分子这个广义集合的组成。这个广义集合的分布函数就是表3.3

表3.3 水分子的分布函数

标志x ：原子序数（或原子量）	H氢的原子序数=1 （原子量=1）	O氧的原子序数=8 （原子量=16）
个体（原子）的数量n：	2	1

水分子由氢二氧一组成，换为新语言就是这个广义集合的分布函数是表3.3。即广义集合概念和分布函数都是描述分子的化学组成的等价语言。当每个化学家发现一个化合物的原子组成时等价于找到了一个广义集合的分布函数。化学家发现了上百万种分子的原子组成，这等价于发现了上百万个分布函数。

如果我们把原子看成是一个广义集合（换了一个层次），而分析每种原子是由那些基本粒子组成的，那么电子、中子、质子就是标志值。而地球上自然存在的近100种的原子中每种都是一个广义集合。这近100种广义集合的差别仅在于广义集合内不同的基本粒子（电子、中子、质子--标志值）的个数不同。例如氢是仅有一个质子和一个电子，而氧有8个质子、8个电子和8个中子等等。这样我们就把广义集合概念用到了另外一个层次的问题中去了。

上面的例子说明化学家200年的努力搞清楚了上百万种化学物质的原子组成、物理学家50年的努力弄明白了不同的原子是由那些基本粒子以什么配方、成分（不同的基本粒子各有多少）组成的（当然他们还在其他方面做了很多工作）。今天看来他们的这些努力都是在找各种的广义集合的分布函数！

为了增加感性认识，表3.4列举了在社会现象和自然现象中的一些广义集合与分布函数的实例（没有给出具体的分布函数的数值）。

表3.4a 社会现象中的一些广义集合与分布函数

广义集合	个体名称	标志名称	分布函数要说明的问题
中国所有家庭	每个家庭	家庭的人口数	不同的人口数的家庭各有多少
地球上的国家	每个国家	国家领土面积	不同面积的国家各有多少
中国的农田	每亩农田	一年的产值	不同产值的农田各有多少
中国的机动车	每辆机动车	车的马力	不同马力的机动车各有多少
中国人	每个中国人	年龄	不同年龄的中国人各有多少
中国在奥运会上获奖	每个奖牌	奖牌等级	不同等级的奖牌各有多少
耀华股票	持有股票的人	持有股票数量	不同数量的股票的股民各有多少
进商场的所有顾客	每位顾客	顾客购物金额	不同购物金额的顾客各有多少
某市一天的电话	每次通话	通话时间长度	不同通话时间的电话各有多少
中国的国营工厂	每个国营工厂	职工人数	不同职工人数的工厂各有多少

不同年龄的中国人各有多少？这是个大问题，而表中恰好用一个广义集合的分布函数描述了这个问题。表中的其他个例也都有启发性。广义集合可以把很多社会问题提清楚，而分布函数可以对问题作出明确的回答。这说明社会科学的研究中应当应用广义集合。

在表中仅给出了广义集合对应的分布函数的物理含义。社会科学工作者应当在这种思路的指引下去寻找分布函数。每找到一个分布函数都意味着发现一个客观规律（定律、经验公式）。函数不是让社会学者讨厌的抽象概念，而是自己的朋友和助手。

表3.4b自然现象中的一些广义集合与分布函数

广义集合	个体名称	标志名称	分布函数要说明的问题
太阳系小行星	每个小行星	行星的质量	不同质量的行星各有多少
中国的煤矿	每个煤矿	煤矿的储煤数量	不同储量的煤矿各有多少
某年的地震	每次地震	地震释放的能量	不同能量的地震各有多少
一次暴雨过程	每平方公里暴雨	雨量	不同雨量的面积各有多少
全国的湖泊	每个湖泊	湖泊的面积	不同面积的湖泊各有多少
全国的土地	每平方公里土地	海拔高度	不同海拔的国土各有多少
一片西瓜地	每个西瓜	西瓜的重量	不同重量的西瓜各有多少
一片松树林	每棵松树	树龄	不同树龄的松树各有多少
人体	体内每段血管	血管的直径	不同直径的血管各有多少
一瓶氧气	每个氧分子	分子运动速度	不同速度的分子各有多少

表里的有些分布函数的数学公式已经被找到了。例如氧气的例子就由物理学家麦克斯威在上世纪从理论上给出了、地震的分布函数也已经被人从地震数据中归纳出来了。如果关于煤矿或石油的储量的理论分布函数已经知道了对我国的开发显然很有指导意义。这都说明广义集合的研究在自然科学中也是非常重要的。在下一章还要介绍关于广义集合和分布函数的更多的例子。它们或许使读者吃惊：我为什么没有想到在自己最熟悉的领域竟然有这么多的数学问题！它们或许使读者兴奋：我今后一定要在用这些新概念和新规律分析我最熟悉的问题。

§3.4从观测数据中求分布函数

我们不仅看到了很多广义集合，也看到了与它相伴的分布函数。现在的问题是每个具体的广义集合的分布函数是如何求得的。

求广义集合的分布函数的途径有两个。一个是从理论上求其分布函数，一个是对客观事实做观测和统计计算求出它的分布函数。从理论上求分布函数是理论工作（如后面介绍的最复杂原理等）的任务，这些以后再谈。现在介绍从观测调查的事实中得到分布函数的方法。

求分布函数首先要弄清楚什么是研究的客观事物（广义集合）、什么是它里面的（我们关注的）个体以及什么是要研究的标志这三个环节（把其他问题都排除在外）。下一步是明确什么是本问题中的“不同的标志值的个体各有多少”。求其分布函数就是回答上面的问题，这道理其实很浅显。

选举是现代政治活动的重要一环，大家对选举的过程也比较熟悉。这里就以它为例说明统计选票也就是求分布函数。首先明确什么是本问题中的广义集合、个体、标志和分布函数。表3.5可以把问题提清楚。

表3.5 用新语言分析选举问题

广义集合	个体名称	标志名称	分布函数
所有的有效选票	每张选票	候选人	不同的候选人各有多少张票

上面的表说明选举过程中投票以后的统计选票的过程就是求分布函数的过程--求得不同的候选人各有多少张票。看来求分布函数并不神秘也不难。

是的，我们对统计选票过程很熟悉。最笨的统计方法是列出两个表。第一个表是原始资料表（即上一章介绍的广义集合的原始列表），它给出了每张选票的原始情况。

表3.6 把选票整理成一个原始列表

选票编号	1	2	3	4	5	6	..	..	..	100
被选举人	A	B	A	D	A	C	A			A

表里共有100张有效选票，而被选举人仅有A、B、C、D四位。利用这个表统计每个人的得票时我们中国人的做法是在黑板上用正字的多少表示每个候选人的票数（正字五笔，每笔代表一张选票，每有一张选票加一笔）。于是就有第二个表。例如它表3.7。

表3.7对原始列表的计票统计

被选举人	A	B	C	D	标志值
得票数	正正正正正正正正正正正正正正正	正正正	正正	正	个体数量
百分比%	75%	15%	10%	5%	合计100%

每个正字代表五张选票，所以四个候选人的得票数分别为75，15，10，5。合计为100。得票百分比的合计为100%

这个表既是选举结果也是由有效选票组成的广义集合的分布函数。它说明了不同的候选人各有多少张票。而A的票最多，他当选了。

实际的选举统计工作可能比我们的做法还要简单，即仅列出第二个表就可以了。我们以一个最简单的例子用了最笨的方法得出了分布函数。其目的是说明从原始资料（也就是从所谓广义集合的原始列表）中求分布函数的过程。

概括地说从资料中求分布函数的步骤是：

1.明确什么是本问题中的广义集合、个体、标志和分布函数的格式；

2.把原始资料(每个个体的标志值）整理成上一章介绍的原始列表；

3.利用表中的原始资料再统计成表3.8形式。

表3.8 把原始列表整理成分布函数的一般格式

标志值	x₁	x₂	x₃	…	x_I	…	x_k
个体数量	n₁	n₂	n₃	…	n_I	…	n_k
百分比	p₁	p₂	p₃	…	p_I	…	p_k

这个表就给出了不同的标志值x_i的个体各有多少n_i，它就是你要的分布函数。利用数学技术和软件还可以把它变成一个曲线、直方图或者一个解析公式。利用后面介绍的广义集合符号化方法、再有计算机帮助，求分布函数更容易。

从资料中（原始列表）求分布函数的道理很简单，做起来有时很繁。但是实际统计工作可能有很多的窍门。在《熵气象学》一书中（1992年气象出版社）有更多的气象上的比较复杂的统计分布函数的例子。

从资料中得到一个分布函数相当于找到了一个经验公式。这本身就是有相当的科学价值。现在有很多工程师可以使用一些书本上现成的公式。但是自己从客观观测数据中发现一个经验公式的工程师并不多。有了广义集合的概念，知道每个广义集合必然伴有一个分布函数，这就为广大的工程师们发现新的公式（分布函数）提供了清楚的思路。

§3.5分布函数的一些性质 回本章首