 | 1.由于分布函数中的函数值的物理含义是本广义集合内的与某个标志值对应的个体的个数，而个体的个数不可能是负数或者有两个值，所以分布函数的函数值都是单值的正数而没有负数。在前面的例子中就是每个候选人的得票数不会是负值。 |
| 2.每个个体必然有一个确定的标志值，所以各个标志值对应的函数值（即对应的个体的个数）的合计必然等于本广义集合的含有的个体的总量。在前面的例子中就是四位候选人的得票总数应当等于有效票的总数100。 |
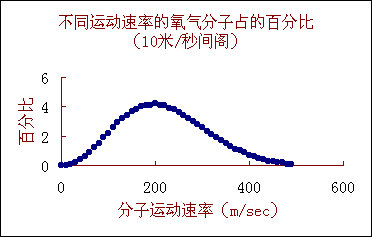
| 3. 如果用个体的总数去除每个函数值，我们当然得到了一串新数，它是相对的函数值，或者说是该种标志值在总体中占的比例（权重、百分比）。我们把这一串新数称为相对分布函数或者权函数。在前面的例子中表3.8 的最后一行就是相对分布函数值。显然相对分布函数的合计值应当等于1（在概率论中这被称为归一性）。 |
| 4.相对分布函数与概率分布有等价性。这个问题很重要，后面将另行说明。 |
| 5.分布函数可以是离散函数也可以是连续的函数。在前面的例子中候选人是标志，而各个候选人（标志值）都是单个的个人。这对应于标志值仅能离散的取值（离散值是字符串变量）。其分布函数也是一些离散（分立）的数。 |
图3.1 不同运动速度（速率）的氧分子占的百分比---连续的分布函数的例子
但是在科学上将会看到很多事例其标志值是连续变量（但是它通常有单位）。这时它们的分布函数很可能也是连续函数。例如常温下氧气的各个分子都是在快速运动，其不同的运动速度占有的不同比例如图所示，它是个连续曲线。这个分布函数里的标志值可以是连续变化的量（对应于概率论中的随机变量），其分布函数通常也是个连续函数。
此时仿照概率论中的做法，我们一般把分布函数改称为密度分布函数。其数学含义是标志值的单位增量所对应的个体的个数的增量。它被个体总量N 除了以后就与概率密度分布函数相同了。
§
3.6 小结讨论某个总体（系统、体系）时经常用到“分布”一词。如果对这个系统的描述精确到广义集合的程度，对分布一词的应用就可以精确到分布函数的水平。分布函数是函数中的一种，它描述一个广义集合内的标志值和它对于的个体的个数的关系。质言之，分布函数就是用于描述广义集合（总体、系统、体系）内具有不同的标志值的个体各有多少个的。它是一个有数学又有物理的概念。
利用关于广义集合的原始列表资料，经过统计处理就可以得到其分布函数。每个广义集合都伴有一个分布函数，是本章最重要的结论。这意味着每认识一个明确的广义集合也就发现了一个分布函数；也意味着分布函数是描述广义集合的一种简明方法。
在科学上每找到一个事物间的函数关系经常意味着发现了一个客观规律（牛顿发现的万有引力就是）。有了广义集合和分布函数的概念也就理清了你在科技领域寻找定量的客观规律的一种思路。
一般把标志值作为分布函数的自变量而把它对应的个体个数作为分布函数的函数值（因变量）。各个自变量所对应的因变量（个体的个数）的合计值应当等于总体内的个体的总量（N）。用N去除分布函数值得到的函数称为相对分布函数。在标志值和个体个数都是连续变量的情况下我们经常研究分布函数对自变量的微分，它被称为密度分布函数。
分布函数可以用表、图或者公式（表达式）等方式表示它。下一章介绍关于广义集合和分布函数的更多的例子。关于它们的符号化和运算规则问题在第六章介绍。对它们的理论分析则放在下一篇介绍。
--第三章结束--