第十七章概率分布的统一（1）     

2001年11月公布于 http://entropy.com.cn 

张学文 zhangxw@mail.xj.cninfo.net 

§17.5几何分布

一个广义集合的标志变量如果仅能取离散的值（如b,b+1，b+2，b+3，…），而且又有类似前面的约束条件，那么最复杂原理引出的分布函数也是类似的。具体地说，有N个个体组成的广义集合，标志变量x的取值如果是b,b+1，b+2，b+3，… 它们对应的个体个数分别是n_0,n₁,n₂,n₃,…,那么类似的约束条件是各个标志变量具有的个体的总量应当等于N ：

N= n₀+n₁+n₂+n₃+…=∑n_i

上面的约束对应前面的公式（17.10），而与（17.11）对应的约束条件是：

a=[b n₀+(b+1)n₁+(b+2)n₂+(b+3)n₃+…]/N

复杂程度C应当是

C=-∑n_iln(n_i/N)

当广义集合具有随机性时，它满足最复杂原理，利用第十二章的拉哥朗日方法，有

  F=-∑n_iln(n_i/N)+C₁(∑n_i-N)+C₂[∑(b+i)n_i-a]

求F对n_i的偏微商，并且令其为零，得到

-lnn_i-1+C₁+C₂b+i C₂=0

前面的b, C₁ C₂ 是常数，以上结果经过整理可以写为

n_i=n₀qⁱ        （i=0,1,2,3） （17.17）

形式。这里的q也是常数。请注意这种写法已经与等比级数公式一致了。它表示标志值为b+i 的个体的数量与标志值的顺序值i成等比级数关系（仍然是指数函数）。由于等比级数也称为几何级数，这可能就是这种分布也称为几何分布的原因。

在《干旱区地理》杂志1991年4期16-21页上，分析新疆无雨期维持的天数的文章就用类似的思路研究了一个具体事例。

§17.6分数维与幂分布（1）

17.6.1分数维问题

20世纪70年代在科学园地出现了所谓“分型几何学”（分数维）这个新词汇，80年代传入我国。分型几何学以新的眼光分析事物，可以横跨众多的学科，形成了一股学术新思潮。它与其他一些新学科一起撼动着牛顿时代以来的科学分类体系的权威性。

B.B.Mandebort 是这个新学科的旗手 。他最早提出了自然界不仅存在一维的直线，两维的平面、三维的立体，还存在维数是分数的所谓分数维。海岸线的维数界于1-2之间就是一个例子。分数维意味着两个量x，y之间存在着幂函数关系,即y=ax^b 。而这里的b可以不是正整数。把数学上早已知道的幂函数戴上了一顶半物理学的新帽子--分数维，它竟然激起了人们的新热情！于是人们在各个领域寻找幂函数关系，并且宣布我发现了某某领域的分数维！这成了科学舞台上的一道景观。这种努力打破了原有的科学分界，推进了科学发展。

人们发现月球上不同直径（x）的陨石坑各有多少（y）、地球上（或者某个区域）不同长度的河流（x）各有多少（y）等等都服从幂函数关系y=ax^b，见表17.2。

表17.2 分布函数为幂函数的自然现象的个例

在分数维的旗下，在这么多学科中找到类似的数学规律，这是分数维研究的一个功绩。

表17.2中列出了一些符合幂分布的“分型”事例。但是“分型”研究中强调的幂关系可能是我们的词汇中的分布函数，也可能指另外的变量之间的幂函数关系。对于后者，下面不做讨论。这里仅分析“分型”研究中揭示的，并且具有分布函数含义的那些幂函数关系。

17.6.2 幂分布是最复杂原理的一种体现

分数维研究以发现这些幂函数而喜。但是为什么幂函数在自然界和社会界的现象中普遍存在？形成这种函数关系的物理原因是什么？遗憾的是，分数维研究并没有正面回答这个问题。

现在我们指出利用最复杂原理和一个特殊的约束条件，就可以从理论上推导出幂函数形式的分布函数来。这样最复杂原理就帮助分型研究找到了不同领域的很多幂分布的共同物理原因。

第十二章分析过斩乱麻问题，在利用最复杂原理求其分布函数时还利用了一个约束条件，就是被切割的麻线总长度是不变的。这个约束实际上等价于求解时要求变量（标志值）的平均值不变。

从数学角度看，一般所谓的平均值实际是指算术平均值，然而我们还可以有其他类型的平均值。实际上只要把算术平均值不变的约束改为几何平均值不变，得到的分布函数就从原来的负指数分布变成了幂函数分布了。

如果一个广义集合的个体总量是N，标志值为连续型的变量，其分布函数（指相对密度分布函数）是f(x)。复杂程度C是

---（17.6a）

与此对应的信息熵H是

---（17.6.b）

这里的a，b是变量的下限和上限。对于相对密度型的分布函数，应当有

--（17.7）

由于几何平均值m的含义是N个体的标志值（变量）x的连乘积再开N次方。在离散情况下的计算公式是

(m^N)=[(x₁)ⁿ¹][(x₂)ⁿ²]…[(x_i)ⁿⁱ]      

这里的n_i是标志值为x_i 的个体的个数。把上式两边取自然对数，有

Nlnm= n₁lnx₁+n₂lnx₂+…n_ilnx_i +…=∑n_ilnx_i 

对于连续变量，其几何平均值m应当与上式类似，即有

  （17.18）

所谓几何平均值不变，在这里的含义就是m是不变量，未知的分布函数f(x) 应当适应上面的约束条件。

如果研究的广义集合本身存在随机性，它就服从最复杂原理，其复杂程度C（或者信息熵）应当自动达到最大值。对于本问题，它还要求满足条件（17.7）和（17.18）。根据拉格朗日方法，用待定常数C₁，C₂分别乘（17.7），（17.18）式再与（17.6）相加得一个新的函数F

F= -∫f(x)[lnf(x )]dx-+C₁[∫f(x)dx-1]+C₂[∫f(x)lnxdx-lnm]

把上式对f求偏微熵，并且令它为零，我们就得到了满足最复杂原理和几何平均值不变的广义集合的分布函数，即

   （17.19a）

这里的常数C₁，C₂应当从约束条件（17.7），（17.18）中求出。由于 exp(-1+C₁) 也是常数，以及常数C₂是变量x的“幂”（C₂次方，power），按照数学习惯称谓，分布函数f(x)与变量x之间就是“幂函数”的关系。这样，我们认识到几何平均值不变（没有更多的约束）的广义集合，如果标志值以最任意、最混乱（复杂程度最大）的方式取值，那么，其分布函数仅能是幂函数形状的。

上面的公式显然也可以写成下面的简练形式（r，s是两个常数）

f(x)=rx^s   (17.19b)

几何平均值的计算公式还使我们认识到变量不仅要大于零，而且不能等于零（否则无法求几何平均值），所以在这一类问题中变量必然存在一个大于零的最小值，它也就是积分的下限值a。

分析实际问题时究竟这个最小值等于什么是与取的变量的单位有关的。我们不妨规定变量的最小值等于1，使问题规范化。如果N个个体中有N-1个个体都取最小值，那么在几何平均值等于m的要求下，余下的唯一的一个变量就必须等于m^N。它也就是标志值的上限值b。这是非常极端的情况。这也提示我们分布函数在b以外的值应当是0。在利用公式（17.7）、（17.18）求C₁，C₂时明确这些会比较方便。

如果规定变量的最小值是1，而变量在积分上限b处的分布函数值为0，可以得到分布函数（相对密度）公式为

      （17.20）

这就是标志变量的最小值为1，几何平均值为m的广义集合在服从最复杂原理情况下的分布函数的具体分布公式（相对密度形式的）。变量下限不是1情况下的公式笔者尚没有得到。

这样我们就从最复杂原理结合具体约束得出了幂函数形式的分布函数，它统一回答了分数维研究中的一些悬案。

图17.4给出了幂分布的图形。它是利用（17.20）公式在最小值为1、几何平均值为5的情况下得到的。图形显示随着标志变量值的增加，它出现的概率在下降。但是它下降的速度比前面介绍的负指数分布要慢。

图17.4幂分布的图形

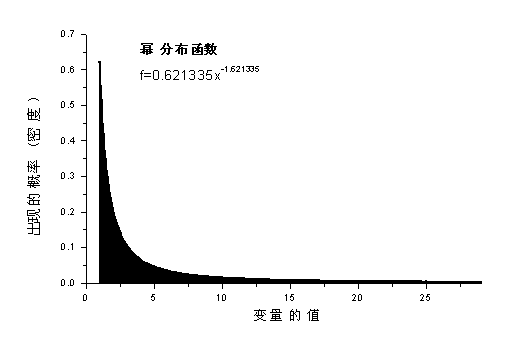
通过上面的分析我们看到分型研究强调的幂分布如果具有分布函数的含义，它就可以从几何平均值不变和最复杂原理的角度推导出来。

17.6.3 初步分析

l         公式（17.19）或者（17.20）是相对密度形式的分布函数，即标志变量的值出现于x-0.5到x+0.5这单位区间内的个体占个体总量的百分比是用这个公式求得的f值。

l         由于变量必须为正值而分布函数的积分必须等于1，这就要求幂的值（即C₂）必须是负的。

l         对公式（17.19）的两边取对数，显然得到：

lnf=(C₁-1)+C₂lnx           (17.21)

由于C₁，C₂都是常数，这个结果说明对变量x和它的出现概率密度f分别取对数以后，两个新变量之间是直线关系。如果用图形检验两个变量是否为幂函数关系，检验它们的对数之间是否在一条直线上就是一个等价又用直观的好办法。

l         如果该广义集合的个体总量是N，那么标志变量出现于x-0.5到x+0.5这单位区间内的个体的实际数量就是Nf。这也就是g(x)=Nf(x)的关系。

l         如果几何平均值很大，-1/(lnm) 就接近于0，上式就简化为

(17.22)

这个公式说明分布函数（相对密度）是变量负一次方。或者说f和x的乘积值是一个常数。这时f和x显然是双曲线关系。在分型研究中把负一次幂称为Zipf律，他们也发现了很多事物服从这个分布。

§17.7幂分布函数的数值模拟