第十七章概率分布的统一（1）

   2001年11月公布于 http://entropy.com.cn 

张学文 zhangxw@mail.xj.cninfo.net

§17.7幂分布函数的数值模拟

 第十二章介绍斩乱麻问题时曾经给出了一种数值实验的方法以获得一个服从负指数随机数值系列。现在我们要给出一种方法，以得到一个服从幂函数分布的数值系列。具体地说，我们要生产一批数据（如数百个），它的几何平均值必须等于给定值m，而各个数据的取值又是最任意、最随机、最混乱的。其做法是（这里给的是标志变量的最小值是1的情况，小做变动也可以推广到任何大于零的实数）

1.         如果变量的最小值是1，几何平均值是m，变量的总个数有N个，令Q=Nlnm 。

2.         利用电脑生产N-1个界于0-1之间的服从均匀分布的随机数—满足最任意的要求，并且分别乘以Q，得到数列A 。MICROSOFT的OFFICE软件中的EXCEL就可以得到这些数。

3.         把数列A的数据按升序由小到大排列，并且在首尾分别补上0和Q，得到数列B。它显应当是N+1个数。

4.         把数列B中的各个相邻的两个数做减法（大减小），就得到具有N个数的数列C。

5.         数列C中的N 个数值有大有小，分别代表了N个标志变量的对数的值。统计不同数值的数据各有多少个（笔者用origin5.0软件）。

6.         设不同的数据x₁,x₂,…,x_k对应的个数分别是 n₁,n₂,…,n_k，把n₁,n₂,…,n_k分别取对数。就得到k对数：(x₁;lnn₁), (x₂;lnn₂)，…，(x_k;lnn_k)在以lnn为纵坐标，x为横坐标的直角坐标图上点上这k个点。

7.         如果这些点都集中在一条直线附近，就说明变量的出现频率的对数与变量x存在直线关系。

8.         把数列C中的各N个变量值x_i分别求exp（x_i）就得到真正的满足几何平均值为m的N个随机数y_i。这些数据才是符合幂分布的标志变量。

9.         对得到的直线求直线拟合公式，对拟合公式中的常数做变换就得到对原始的标志变量的幂分布公式。

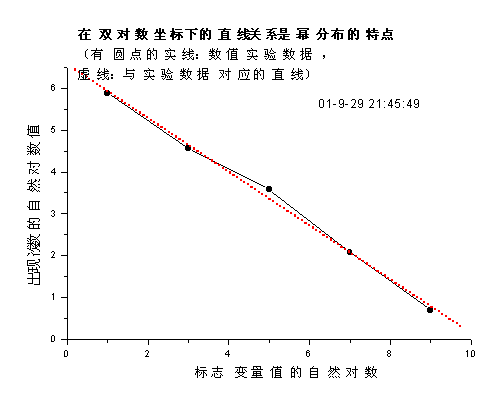
图17.5是我们做的一个数值模拟实验。我们取其几何平均值为5，最小值是1，数据个数是500。图中有圆点的实线（折线）是实验数据的实际值，而虚线是对这个结果再模拟出来的直线。我们看到实际的折线与选配的直线非常接近。它说明标志值取对数以后确实与其出现次数的对数值是直线关系。而依照前面的分析，这正是幂分布函数的特点。所以这个直线说明了原变量服从幂分布。

图17.5对幂分布的一个数值实验结果

       为什么这样做数值实验得到的数据满足最初的设定？细说每个环节费笔墨，现在仅分析这个数据的各个变量的几何平均值是什么。

数列C包括了500个数据。根据操作的步骤，这些数据的合计值显然等于500ln5。即

500ln5=∑x_i

上面的求和对应500个数相加。我们曾经利用 exp(x_i)=y_i 得到了500个y_i 的值。并且说y_i 就是符合幂分布的数列。而根据这里的关系显然ln y_i= x_i 。于是

500ln5=∑x_i =∑lny_i

利用对数相加等于各个变量相乘再取对数的性质，有

500ln5=ln(y₁×y₂×y₃×…×y₅₀₀)

ln5⁵⁰⁰= ln(y₁×y₂×y₃×…×y₅₀₀)

所以

5⁵⁰⁰= y₁×y₂×y₃×…×y₅₀₀

上面的关系说明500个变量的连乘积的值恰好等于5的500次方，根据几何平均值的定义，这说明500个变量的几何平均值就是5。所以最初的那些步骤保证了得到的数列的几何平均值等于预先的给定值。

这个数值实验说明在几何平均值为固定值，并且具有最任意、最混乱、最随机的数列（广义集合）的分布函数与相同约束下从最复杂原理得到的理论分布函数是一致的。即数值实验证实了最复杂原理的一种推论是正确的。

§17.8分数维与幂分布（2）

前面用最复杂原理说明了幂分布函数的物理原因，也使分型几何学得到了一部分物理解释。另外，我们还注意到分型几何学强调“自相似”这一个重要性质。

孙广元教授为日本学者写的《分数维》的中译本作序，他写到：

“自相似”是自然界普遍存在的现象。在一个系统中，整体和部分之间，这一部分和那一部分之间都具有相似性。如一棵大树，树上任取一枝杈和树的整体具有明显相似性；冬季窗户上的冰花，任取一部分和其整个在结构上亦有明显的相似性；一个水系任取一个支流其分支结构和任一级河网结构间具有明显相似性。…

对幂函数做一些分析会把自相似问题看得清楚一些。

如果把幂分布函数的两边取对数，再取微分，可以得到

dlnf= C₂dlnx

注意到对数的微分具有变量微分与原量的比值的含义, 即

dlnx=dx/x  ,dlnf=df/f

所以 [(df/f)/(dx/x)]= C₂

注意到C₂是一个常数，我们看到分布函数的相对变化（即df/f）与变量的相对变化dx/x 成线性关系（不是与变量本身成线性关系！）。把它翻译为物理语言就是该系统有自相似性质。

自相似性则是分数维的重要性质。说得再通俗些就是某系统（广义集合）中标志变量的相对改变量（dx/x）与其对应的个体的相对数量的改变量（df/f）是正比例关系。

       问题也可以反过来考虑：如果一个广义集合的标志变量的相对改变量与它们对应的数量的改变量成正比例，那么其分布函数应当是幂函数。这样我们就对于自相似与幂分布的内在关系加深了认识。

我们愿意为分型研究发现的大批幂函数分布而鼓掌，我们也希望他们注意到最复杂原理可以为其中不少幂分布做出统一的物理学说明。认识到这些对双方都有好处。

大批自然与社会现象中广泛存在着幂分布函数，这说明最复杂原理在很多领域约束着客观事物。不利用最复杂原理就难以对这么多不同领域的事物符合相同的数学公式的物理原因给出说明。我们应当认识到最复杂原理横跨很多科学门类的能力几乎是牛顿力学所不及的。

       现在社会看重“学历”，于是伪造学历的事就出现了。现在分型研究热，于是一些不是幂分布的自然现象也被拉进了分型研究中，这显然是不正确的。

例如地震所释放的能量（标志变量）与地震出现的次数之间是负指数关系，在数学语言中负指数函数与幂函数不是一个概念（负指数与负的幂在函数图形的重要部分有类似性），但是一些文献中就用“幂指数”这种混淆视听的词装进了分型几何园地。

       又如已经知道某些广义集合的分布函数服从所谓韦伯（Weibull）分布，某些分型研究把这个函数做级数展开，然后针对其中的一小段，说它符合幂分布。这种做法显然很片面。

我们要认识到幂分布仅是很多种分布中的一种，勉强把一切分布都拉进分型研究的范围内不仅与事实不符，也使自己离开科学走向偏见。

       地震现象服从负指数分布，它是最复杂原理和地球在一定时期释放的总能量为常数的必然结果。为什么一些现象符合韦伯（Weibull）分布？我们在后面也可以从最复杂原理引出。

       我们用了一些篇幅谈论了分型几何学的事，并且利用最复杂原理帮助理解他们揭示的一些规律。分型几何学的内容十分丰富。笔者学识有限分型几何学的很多内容我们也没有也无力涉及。有不妥之处欢迎讨论。

§17.9 小结与讨论

l         概率论和统计学中广泛应用着十多种重要的概率（或者概率密度）分布函数。但是没有统一说明它们形成的原因。本章利用最复杂原理配合不同的约束条件推导出5种概率分布。为这些概率分布的形成给出了统一的物理解释，也推进了概率论知识的系统化。

l         用最复杂原理推导这5种概率分布时所利用的约束条件列于下表17.3中。

表17.3 5种概率分布的形成背景

l         对应5种分布，我们明确了对应的约束条件，它们都是非常简单的约束，每个约束在概率公式中体现为物理意义清楚的参数。最复杂原理不仅帮助得到了这些对应的分布，它也意味着：只要该系统满足而且仅仅满足给定是约束条件，那么你就不可能再找到另外一个概率分布函数，其复杂程度比这里给的分布函数所对应的复杂程度更大。理解这层含意会使我们对得到的结果有深刻的物理认识，而不把这些看作是数学游戏。

l         这5个不同的分布让我们认识到约束条件不同，与最复杂原理相伴的分布函数也不同。它说明具体准确分析约束条件是我们研究问题的非常重要的一个环节。不具体解决约束条件究竟是什么，就没有办法定量应用最复杂原理（熵原理）。

l         最复杂原理配合代数平均值不变的约束对应着负指数分布，配合几何平均值不变就对应幂分布，这是前面得到的结论。于是人们问如何判断一个物理系统（广义集合）中其平均值不变是指代数平均值还是指几何平均值？

一般而言，代数平均值不变都与总量不变等价。斩乱麻问题中原线的总长度不变是很明显的约束条件。在那里你无法推断该事物具有几何平均值（各个变量相乘后再开方）具有不变的特点。在统计物理学中，平均值不变常常对应着总能量或者总质量不变。

对于几何平均值，首先要求变量必需是大于零的量。如果一个变量的值是0，或者是负的，就造成了无法开方，或者无法取对数的问题。变量要大于0是个有深刻物理意义的要求。所以当你假设一个变量的几何平均值不变时，最低的要求是它仅能取正值。另外，分型研究提出的自相似性质（见上节）也是帮助判断问题的一个角度。

下一章我们继续介绍另外一些概率分布，它们都是最复杂原理配合另外的约束条件下的必然推论。

第十八章概率分布的统一（2）a