第十七章概率分布的统一（1）

   2001年11月公布于 http://entropy.com.cn 

张学文 zhangxw@mail.xj.cninfo.net

§17.1引论

统计学和它的理论基础概率论现在广泛应用于各个领域。在这些应用中关于离散变量和连续变量的概率分布函数是其重要内容。这些概率分布函数中应用最广的大约有十多种。

利用实际数据分析出某自然现象服从某种概率统计分布、并且找到了它对应的数学公式是一项很好的科技工作。但是没有进一步的物理分析说明，仅为数据选配概率分布函数就可能被认为是一种数学游戏。难怪日本著名统计学加赤池弘次说“统计学的课本往往被看做应用上有用方法的大杂烩”（《数学译林》，“统计与熵”，1984，（2）141-153）。

统计学应用的范围如此之广，它们用的基本概率公式的数量又不多，这里面的深刻原因在目前主流统计学和概率论中是没有给我们指明的。人们期待一个理论可以对此做统一的说明 。确实，人们期待着统计学能够对客观规律提供更有物理意义的理论解释。

组成论的出现使我们有的新视角：具有概率特点的客观事物本身应当具有随机性。有随机性的研究对象（广义集合）都应当遵守最复杂原理。那么最复杂原理是否可以对目前的统计学情况有所改进？

第十七和第十八章就正面回答这个问题。我们要从最复杂原理配合不同的约束条件，从理论上推导出概率论中常见的若干概率分布函数。这为分散的概率分布函数找到了统一的，系统的物理的说明，也使概率分布的理论成因的物理背景清楚了一大步。

人们对牛顿的力学公式配合不同的约束条件从而得到了例如直线运动、等加速度运动、圆周运动、抛物线运动留有深刻印象。是的，各种具体的运动规律都符合牛顿力学公式，这恰好说明牛顿公式在力学中的核心地位。

在分析由多个个体组成的系统中各个成分占的百分比时，如果系统具有随机性，就可以利用最复杂原理（熵原理）配合不同的约束条件得到不同的分布函数。而这一类函数在一些场合（一些视角下）就是概率分布函数。最复杂原理（熵原理）在大量粒子组成的有随机性的系统中的地位几乎与牛顿公式在简单力学系统的地位是相当的。

确实，热力学第二定律被爱因斯坦说成是宇宙的基本法则。第二定律就是关于熵的定律，我们说的最复杂原理也就是在更广泛领域使用的熵原理。所以我们认为把一个具体客观规律（如某自然现象遵守正态分布函数）用最复杂原理给予说明，这个答案的理论地位应当与另外一个问题（例如真空中的自由落体做等加速度运动）被牛顿力学给予说明是相同的。1992年笔者说“用最大熵原理阐明的事理与用力学原理阐明的事理至少在离终极真理的距离是一样的近。”（见《熵气象学》131页）。

用最复杂原理（最大熵原理）有可能具体说明各种概率分布的理论成因，所以这个原理应当在概率论和统计学中占有重要地位。概率论和统计学应当欢迎这种认识，而不是排斥这个认识。

§17.2等权分布

等权分布是最复杂原理用于离散的情况下的一个特例。

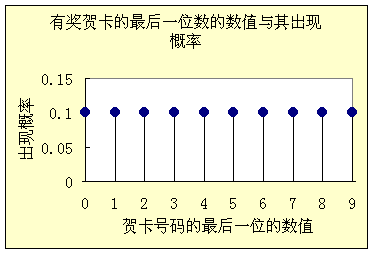
新年时收到了100张有数码（有奖）的贺年卡。如果我们研究贺年卡数码的最后一位（0，1，…，9）究竟是几，可能提出一个问题：在最可能的情况下，不同的末位数码的贺年卡各有多少张？

什么是最可能？它也就是出现概率最高、该广义集合的复杂程度最大。由于得到的贺年卡有随机性，所以可以利用最复杂原理（保证复杂程度最大）求不同数码的贺年卡各有多少张（即求一个分布函数）。

把100张贺年卡看成是一个广义集合。最后一位的数码有0，1，…，9 计10种不同的值（标志值），把最后一位的值是0，…，9的贺年卡的张数分别用m₀，m₁，m₂，…，m₉ 表示。显然有

m₀+m₁+m₂+…+m₉=100张---(17.1)

成立。

这个广义集合的复杂程度C，根据复杂程度公式（7.5），即

--（17.2）

结合本问题，它应当等于

C=- m₀ [ln（m₀/100）]- m₁ [ln（m₁/100）]-…-m₉[ln（m₉/100）]

为了利用复杂程度C最大（最复杂）反求分布函数（也就是求不同末位数码的贺卡张数m_i），根据第十二章第5节关于拉格朗日方法的介绍，本问题中的约束条件仅有一个，即公式（17.1），我们构造一个新函数F

F=C+C₁（m₀+m₁+m₂+…+m₉-100）    （17.3）

C₁是一个未知的常数（不要与复杂程度的C混淆！）。根据（17.1），（m₀+m₁+m₂+…+m₉-100）与C₁相乘的数显然仍然是零，所以复杂程度C最大与F最大是一致的。但是，从另外的角度看，F现在是各个m的函数了。求F最大就是把它对m_i求偏微熵（在i=0，1，…9这10个情况下分别做）并且利用F最大时这些偏微熵等于零的条件，而有（参考拉格朗日方法的介绍，或者自己去参考有关的数学书籍--这大约是大学理科一、二年级的数学教学内容）：

0=-ln(m_i /100)-1+ C₁    （i=0，1，…9）

上面的等式实际有10个（i=0，1，…9），由于各个m_i都满足相同的关系，显然要求各个m_i的值相等。利用关系（17.1），得到

m_i =（100/10）=10              （i=0，1，…9）

即无论i等于1或者2或者3…或者9，m_i都等于10 。

这个结果的含义是在贺年卡有随机性的情况下复杂性最大、熵最大、可能性（概率）最大、最混乱的结果是末位数为0或者1或者…或者9的明信片都是10张。即各种末位数码的明信片占的比例或者说权重（百分比）都相同。用我们的术语说就是各种标志值的个体的数量（分布函数值）都相同（相等）。我们把分布函数的值不随标志值而变化的这种分布函数称为等权分布（“权”字的含义就是比例、比重、权重）。

如果用横坐标上的一些孤立的点表示标志值，用纵坐标的长度表示广义集合中该标志值的个体占的数量（或者权重），那么这个图上的等权分布就是立着的一排长度都相等的小棍。

图17.1等权分布函数的例子

n_i=N/k    （i =1，2，…，k）     （17.4）

即不同的标志值占有的个体数量（权重、百分比）都相同。

换为概率语言就是随机变量仅可能取k个值时，每个取值的出现概率都恰好是1/k的等权分布是最可能出现的结局，这也是该广义集合的复杂程度最大时的结局。即其他结局的出现概率和复杂性都没有它大。写为公式就是

p_i=1/k     (i=1，2，…，k)   （17.5）

本分布对应于概率分布中的等概率分布。

结局个数为有限值，并且概率分布对应的复杂程度最大的分布是等概率分布。

10个学生谁会考第一？在没有其他约束（知识）的条件下，我们仅能说每个人考第一的概率是相同的。没有进一步的知识的情况下，有k种可能结局，我们假设每种结局的出现概率都相同就是一个明智的选择（出错最少）记得这被称为拉普拉斯原理（找不出充足的理由说谁的可能性更大）。

气象观测要求把空气温度测量到小数点后面的1位。而这最后1位显然与空气温度的随机性有关。如果某观测员的1000次观测中最后1位的数码是“5”的竟然占了40%，根据最复杂原理，（与明信片问题一个道理）数码“5”仅占10%，所以这些数据显然有弊！

根据最复杂原理求得的不同的末位数码的有奖贺年卡的数量可能与实际有差别。但是当收到的贺年卡的数量越大，这个结果越符合实际。盒子里有10个格子，把10²⁰个气体分子放到盒子里。每个格子的分子个数是几乎相等的可能性大还是有的格子分子很多，有的几乎没有分子的可能性大？当然是每个格子里的分子的个数都相等的可能性最大（否则我们住的房子早就爆炸了或者变成真空了！）。统计力学中推导分子在格子中的个数的公式（即分布函数）的过程与这里的贺年卡末位码问题是相同的。在统计力学里这被称为微正则分布。不考虑最复杂原理（熵原理），把各个状态出现的机会都相等作为一个基本假设也可以搭起统计力学中的一些知识框架。

等权分布或者称为等概率分布、微正则分布是最基本最简单的一种分布。我们定义广义集合的个体时强调每个个体的地位相同，也就是要保证每个个体在总体中的地位相同（等权）。此时，对广义集合的个体做随机抽样，每个个体被抽中的概率也就必然相等。

§17.3均匀分布

等权分布是在标志值为离散取值（分立）的情况下得到的。如果变量（标志值）是连续变量，而其他的约束条件类似，就得到了这里介绍的均匀分布。均匀分布就是标志值为连续变量时的一种广义集合的分布函数。

上一节引的贺年卡的例子实际上是限定了明信片的末位号码仅可能是10个数码中的一个，即标志值仅可能有有限的10个值。与此对应的连续变量（标志值）则是变量限定出现于某个区间。对应的问题成了下面的形状。

某广义集合中有N个个体，每个个体的标志值（变量）仅出现于从a到b的区间（上）内，当广义集合的标志值究竟取什么值具有随机性时，问：此广义集合的复杂程度最大时，具有不同的标志值（实为出现于不同的小区间的标志值）的个体分别是有多少（对应于求一个分布函数，知道一个具体的组成情况）？

用拉格朗日方法处理这个问题的步骤与“斩乱麻”例子中的做法类似：

当标志值是连续变量时，经常用相对密度分布函数 f(x)，即标志值出现于x-0.5，到x+0.5区间（单位增量）的个体的百分比是f(x)乘1（单位增量），而出现在这个区间的个体的个数是N f(x)。其复杂程度C为

       （17.6）

而本问题对应的约束仅有下面一个：

             （17.7）

由于变量仅出现于a，b区间上（内），其分布函数f(x)仅在区间上（内）有值。由于在区间外其函数值都是0，所以上面两个积分仅在a，b内进行就足够了 。依拉格朗日方法，把未知的常数C₁乘（17.7）再与（17.6）相加得到F

            (17.8)

由于复杂程度C最大与F最大是等价的。我们求F对f 的偏微熵（它的含义是改变函数f的形状但是x不变，这实际是所谓求泛函数的极值，即变分），并且令它等于零（使F极大），就得到

Nlnf(x)= C₁-1

它表明分布密度函数f(x)仅能是一个不变的数，而不是随x而变化的函数。利用关系（17.7），得到

f=1/(b-a)        标志值在区间b-a内（上）（17.9a）

f=0，            标志值在区间外                  (17.9b)

用图表示这个函数，它在区间上是一条与变量x 的轴平行的一段水平线，其高度是1/(b-a) ，而在其他地方它与x轴重合。

你家的钟的秒针在什么位置？它肯定出现于0-60秒之间。由于提问题时的具体时间有随机性，所以秒针出现于各个位置的概率遵守一个分布。当仅仅知道它必然在0-60之间，而且有随机性时，就得到均匀分布（图17.2）。

图17.2 均匀分布函数的例子

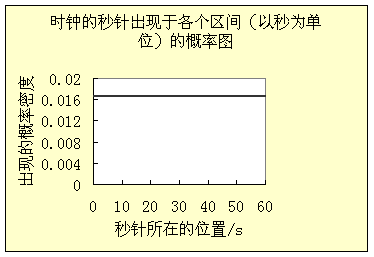
这个结果说明在区间内标志值为各种值的概率是相同的。由于标志变量均匀地分布在区间中，故称为均匀分布。这个名称也与概率论中的概率密度分布函数为均匀分布是对应的。

连续变量情况下的均匀分布与离散变量情况下的等权分布是对应的。它们都是概率论中基本分布。现在的电脑统计计算软件中大都具有生成一批服从均匀分布规律的随机数的现成的小程序。它有助于我们做一些随机性的试验。

例如微软公司的Excel97软件中，利用“=RAND()”函数命令就可以生成一个界于0-1之间的随机数。表17.1就是从中得到的30个随机数。

表17.1用软件生成的30个随机数

§17.4负指数分布

第十二章曾经得到了满足最复杂原理和i个约束关系的广义集合的分布函数（相对密度）应当是

f (x)=exp[-1+∑C_iu_i(x)]        (12.7)

这里的C_i是i个未知常数。而u_i(x)代表i个已经知道的函数，而且这个函数与分布函数的乘积的积分为常数k_i （所有才称它们为约束条件），即有

k_i=∫u_i(x)f(x)dx ， i=1,2,…, m   （12.4）

如果现在我们具体地把约束条件限定为下面的两个：

      （17.10）

   （17.11）

与此约束条件对应的函数显然是

u₁=1              （17.12）

u₂=x        （17.13）

我们把这两个具体函数代入（12.7）式，也就得到了具体满足这两个约束并且符合最复杂原理的广义集合的分布函数，即有

f (x)=exp[-1+C₁+C₂x]    （17.14）

目前上式中的两个常数C₁，C₂的值还不知道。但是利用（17.10），（17.11）这两个关系容易得到

              （17.15）

于是得到结论：广义集合的分布函数（相对密度形式的）如果应当满足（17.10）和（17.11）的关系，并且其复杂程度最大，那么其分布函数（相对密度）就必然是公式（17.15），即它是一个负指数函数。

约束条件（17.10）还表示了一层含义，那就是变量本身必然是大于零的正数。

上面得到的公式是面对相对密度分布函数的。如果广义集合有N个个体，用分布函数g(x)表示标志变量界于x-0.5到x+0.5之间（单位增量）个体的个数，显然分布函数g(x)=Nf(x),那么用g(x)表示（不是用相对密度，仅是用密度分布函数）的负指数分布就是

              （17.16）

细心的读者会发现这里得到的结果与第十二章关于“斩乱麻”的例子是相同的[见（12.11）式]。所以本节仅是用略微不同的语言，重复了第十二章讨论的问题。

图17.3 负指数分布函数
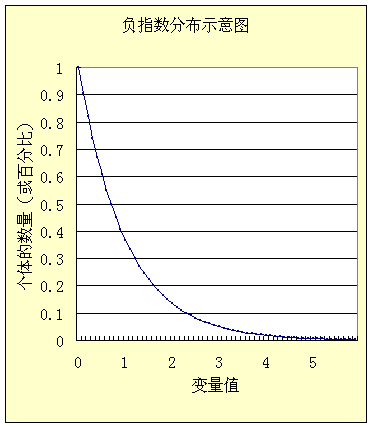
公式（17.15）或者（17.16）都体现了标志变量x的值越小，它占有的个体的数量越多（g，f的值越大），标志变量值越大，具有该标志值的个体的数量就越少(图17.3)。

斩乱麻是负指数分布的生动例子，但类似的例子还有很多。如果有一桶水用最任意（最混乱、最随机）的方式洒到了一个布满了小水杯的地面上，得到水的小水杯有N个，而水的总量为V（一桶水的体积）。这就对应负指数分布所要求的两个约束条件。在复杂程度最大的情况下（满足最复杂原理）得到不同水量的小水杯的个数就应当符合负指数分布。这个思路我们曾经用于降水过程。对很多的大降水过程的实际雨量的分析证实，多数地区雨量很少，少数地区雨量很多，不同雨量与其占的地域面积恰好符合负指数关系。

在一定的温度下、一定量的气体分子具有的运动能量的总和是个固定值，而分子个数也是不变量。当分子的能量在各个分子中呈现最复杂的分布时，最复杂原理是有效的，在前面的两个约束下，分子的能量也应当符合负指数分布。这就是物理学中著名的麦克斯威—玻尔兹曼分子能量分布率。

你把1000粒花生米扔给20个猴子，它们会把花生米平分？不，在最任意的情况下，有的抢了很多，有的得到的很少。“最任意”对应于结局的“最复杂”，于是利用最复杂原理也得到了负指数分布：多数的猴子得到很少，少数的得到了很多。

一个社会具有有限的人数和有限的财富----这对应前面的两个约束条件。如果没有更多的约束（见第二十一章再讨论），最复杂原理告诉我们财富在人群中应当服从负指数分布：多数人贫穷，少数人是富翁。我们对今日中国的财富在人群中的分配状况都不陌生，它很可能是最复杂原理的又一个生动的例子（本人无意为这种不公平辩护，而这里的结果反而提醒政治家：不为社会增加适当的新约束，这社会就没有公平--它会自动地出现所谓两极分化）。

§17.5几何分布