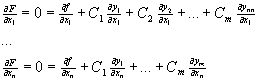
§
12.4拉格朗日方法(1)与前面的一般的求函数极值的方法比,拉格朗日方法最重要的一个技巧是在求极值时可以附加一些约束条件。另外它可以用于求函数极值也可以用于求泛函数极值。本节介绍引入约束条件的思路和方法。
拉格朗日方法在一些理工科大学的数学教科书中有介绍。这里的简单介绍参考了王彬在《熵与信息》书中写法(该书是高等学校教材,西北工业大学出版社,
1994)。欲求
n元函数f(x1,x2,…,xn)在如下m个约束条件(m<n)下的极值(大小),即找出各个
x 分别取什么值时f 达到极值。与前面讨论的一般的求极大值的方法比,这里不是求一元函数的极值,而是求n元函数。另外还补充了m个约束条件方程。拉格朗日方法是以
1,C1 ,C2 ,…,Cm 这些未知常数(待求的)顺次乘f,y1 ,y2 ,…,ym, 并且把它们加起来,就得到了一个新的函数F(大写)。F(x1
,x2,…,xn)=f(x1,x2,…,xn)+C1y1(x1 ,x2 ,…)+C2y2(x1 ,x2 ,…)+…+Cmym(x1 ,x2 ,…) (12.2)
注意到关于
y 的各个函数都是零,所以新函数F 达到极值与原函数f 达到极值对自变量(各个x 值)的值是相同的。函数
F 既然是各个x 的函数,它达到极值时必然是对各个自变量x 的偏微商分别等于零(由于是多元函数,所以过去的微分变成了偏微商了)。根据这个分析,求多个偏微商以后我们就得到n 个新的方程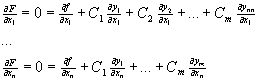
很显然,这
n 个方程式已经巧妙地把约束条件融合到求解的要求之中了。拉格朗日就是这样把约束条件的信息放到了求解进程中了。上面的
n 个方程连同约束条件给的m 个方程式已经可以解出n+m 个未知数。它们就是n 个x(即x1,x2,…,xn)和m 个C (即C1 ,C2 ,…,Cm )。于是我们就得到了这个函数达到极值时的各个自变量的值。可以看到约束条件不同,得到的各个x 值也不同。这样就利用拉格朗日方法解决了问题。下面用王彬书中的例子说明它的应用。
§
12.5例子问题:给你一块面积固定(等于
a 的平方)板子,问做成什么样的长方体(盒子),它具有最大的体积。设长方体的三个棱长为
x,y,z,则其体积f 为三个边长的乘积:f(x,y,z)=xyz
本问题要求表面积为
a 的平方,于是长方体的6面的面积可以写成2xy+2xz+2yz=a2
即 2xy+2xz+2yz-a2=0它也就是本问题中仅有一个约束条件。根据前面介绍的拉格朗日方法制造一个新函数
F,并且放进一个未知的常数C ,于是有F=xyz+C(2xy+2xz+2yz-a2)
令其对
x,y,z 的三个自变量的偏微熵分别为零,得到三个新方程式:yz+2C(y+z)=0
xz+2C(x+z)=0
xy+2C(x+y)=0
(x/y)=(x+z)/(y+z)
(y/z)=(x+y)/(x+z)
由此得出只有各个自变量的值相等才可以维持上面的关系,再由约束条件得到它们的值是
x=y=z=(a/
√6)这就是本问题的答案,它说明表面积固定的长方体的体积最大的形状是正方体。很显然,这与我们的一般认识是相符的。
§
12.6 拉格朗日方法(2)现在把拉格朗日方法与最复杂原理结合起来,并且以求出分布函数为目标。对标志值(自变量)的特点也从前面的离散型转为连续型。这里尽管用到的数学多一些,但是基本思路与前面是一致的。
前面的很多讨论都是以离散变量(不连续的标志值)为主线,这对不熟悉微积分的读者比较容易理解,也不失准确性。但在自然科学中有很多情况用连续变量比较方便。后面也主要讨论连续变量的问题。现在针对连续变量再介绍类似的拉格朗日方法。学习过微积分的读者,读这些比较容易。对于没有学习过微积分的读者就有困难。我们认为克服这个困难的任务应当由读者阅读其他的书籍,而我们就回避细说其中的缘由了。希望读者理解现在的重点并不是重复那些基本数学知识。当然我们也努力写得让没有学过微积分的读者领会基本精神。连续变量的复杂程度公式是
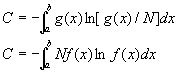
这个积分从分布函数的标志值
x的下限a积到上限b。它代替了离散情况下求和形式的计算公式。这里g(x)表示对应的密度分布函数;f(x)表示相对密度分布函数。即标志值x增加单位值时个体的对应增加量。g(x)与Δx的乘积对应于标志值出现于x→x+Δx区间时个体的数量;f(x)Δx对应于标志值出现于x→x+Δx区间时个体数量占的的百分比(概率)。最复杂原理或者最大熵原理是说上述积分达到极大值。现在的目标是利用这个积分(泛函数的值)达到极大值反求目前还不知道的分布函数
f(x) 或者g(x)。拉格朗日方法可以达到目的。在前面的离散场合的例子里拉格朗日方法是针对一个已知的多元函数
f(x,y,z)=xyz,求自变量x,y,z在什么值时函数值(复杂程度)极大。在连续变量场合拉格朗日方法就是直接求一个未知函数(分布函数)使复杂程度最大。在连续变量情况下约束条件的形式也有一些变化。它们一般以积分的形式给出
(下面都以相对密度分布函数f(x)的形式讨论它们):ki=
∫ui(x)f(x)dx , i=1,2,…, m (12.4)这里共有例如
m个约束,各个ki是一些常数(i表示第i个,它们共有m个),而ui(x)是已知的函数(第i个,共有m个)。f(x)是待求的分布函数(实际是相对密度分布函数,后面都简称为分布函数)。在
m 个方程的约束下,利用复杂程度C 最大(复杂程度最大值是-∫f(x)ln[f(x)]dx最大值的N 倍,但是两者同时达到极大值,所以求谁的极大值的结果都是相同的。为了简化问题,我们在后面就省去了N 这个常数)。求分布函数的方法也是构造一个类似的新函数FF=-
∫f(x)ln[f(x)]dx +∑Ci(∫ui(x)f(x)dx -ki) (12.5)上面的新函数
F 是复杂程度(省了N)表达式与各个约束条件的合计值(每个约束条件都补充一个未知系数Ci ),求和是从i=1到m 。显然,使F 最(极)大也就是使复杂程度C 最(极)大。现在F 的值是未知函数f 的函数(泛函数)。问题变成了未知函数是什么时F 极大(复杂程度极大)。为此,求F 对f 的偏微熵。并且令它为零就可以了。注意到lnf 对f 的微商等于1/f ,以及复合函数的微商公式,我们可以得到:-[lnf(x)+1]+
∑Ciui(x)=0 (12.6) 可以把它改写为f(x)=exp[-1+
∑Ciui(x)] (12.7)由于各个
ui都是已知函数,所以未知函数f (x) 的解已经得到了。即至少我们已经在形式上求得了分布函数的解。现在没有解决的问题是各个Ci的值还不知道。它可以利用m个约束条件去求得。如果把
(12.6)式的左侧再对f 求偏微商,即得到F 对f 的两次偏微熵,它等于-1/f(x)
由于分布函数都必然大于零所以这个函数必然小于零。根据前面关于极值问题的一般知识,这里得到的极值是极大值。即它对应复杂程度的极(最)大值不是极(最)小值。
连续变量情况下用拉格朗日求复杂程度极值的过程这是这些。这里的解不是一个数值或者多个数值,而是一个连续函数。这是它与离散情况的主要差别。即利用它可以得到待求的分布函数。
公式
(12.7)是我们得到的利用最复杂原理反求分布函数的一般公式,后面要反复用到。在公式中我们再一次看到复杂程度取极大值时的分布函数究竟是什么形状,是依赖于约束条件的。即不同的约束条件[不同的ui(x)]对应不同的分布函数。在经典力学那里,牛顿第二定律与不同的初始条件和边界条件结合我们会得到不同的运动规律,例如等速运动、等加速运动、圆周运动、抛物线运动等等;在后面第三篇我们会看到最复杂原理与不同的约束条件配合也得到不同的分布函数。这种类似性已经预示了最复杂原理的广泛用途。
这么介绍比较抽象,下节的例子可以帮助理解做法和结果。
----§12.7 斩乱麻问题----