
第十二章拉格朗日方法(2001.02-03)
§12.1
用最复杂原理寻找分布函数 |
过去利用牛顿力学和数学工具得到了很多不同的运动规律。 现在利用最复杂原理和数学工具也可以得到很多不同的分布规律(函数)。 |
§
12.1 用最复杂原理寻找分布函数 第一篇说明很多(不是全部)客观事物可以用广义集合来描述。由于每个广义集合都伴有一个明确的分布函数,还由于寻找和获得分布函数就意味着在科学上取得了成绩(成就),所以,每当把某些客观事物归结为广义集合以后的一个重要目标就是找出该广义集合的分布函数。对于有随机性的广义集合,由于它服从最复杂原理,这就提出了一个新的普遍适用的思路:利用最复杂原理从理论上寻出广义集合的分布函数。本章讨论利用最复杂原理寻找分布函数的一般方法。它在各种场合的具体应用问题在第三篇讨论。
如何利用最复杂原理寻找出广义集合的分布函数?这里既有物理思路问题也有比较特殊的数学问题。
§
12.2 泛函数和它的极值 1+5=?其答案是一个数。“数”是小学数学题的典型答案。中学里引入函数概念,如y=x2就是一个函数关系,每给定一个x的值(例如代表正方形的边长)就得到一个对应的y值(正方形的面积)。我们把x称为自变量,把y称为x的函数(因变量),并且抽象地记为y=f(x) 。利用函数关系求未知数是中学数学的典型问题。在上一节提出的的目标是在寻找未知的函数(分布函数),而不是寻找未知数。这个目标就超出了中学数学。是的,中学数学经常利用函数关系求未知数,我们要利用所谓泛函数求未知函数。这里先对泛函数概念做简要说明。
在平面上有一条封闭的线绳(L),线绳所包围的面积(图12.1的阴影区的面积)就是一个数。如果线绳的形状变化了,它包围的面积也在变化。形状与面积的关系类似于例如y=f(x)的函数关系,但是这里的自变量不是一个数x,而是线绳形状L。线绳的形状如何用数学语言描述?根据解析几何学知识,它对应于一个函数。于是我们看到一个新问题:因变量(面积)的值在随着一个函数(形状)的变化而变化。现在线绳形状的地位对应过去的自变量的地位。我们把自变量是一个函数时的函数关系称为泛函数关系。图12.1 闭合的线绳包围的面积随着线绳的形状而变化,

墙上两个钉子上有一段绳子,绳子的形状显然决定了线绳的总位能,于是位能就是由线绳形状决定的一个泛函数,这又是一个泛函数的例子。在有关的数学书籍里可以找到很多例子。
第七章得出的复杂程度C的公式是:![]() (
(
这是针对离散型的变量的公式。对于连续变量,前面的求和被积分代替为:
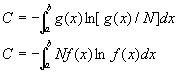
大家比较熟悉求函数的极值问题:未知的自变量等于什么值时,函数的值达到极大或者极小。这个问题的答案显然是在寻找一个特殊的点使其函数值极大(小)。
对于泛函数,也有类似的极值问题:未知的函数等于什么函数时,泛函数的值达到极大或者极小。这个问题的答案显然是在寻找一个特殊的函数使泛函数极大(小)。
例如,对于图12.1中的线绳,我们问线绳是什么形状(函数)时它包围的面积最大,或者第二个例子中问线绳在什么形状下,它的总位能是最小的。这些问题的答案都是寻找一个特殊的未知函数(形状,或者说函数关系)而不是寻找一个点。最复杂原理告诉我们很多广义集合的复杂程度自动取极大值,现在我们反过来应用这个原理:预先承认复杂程度最大(泛函数的极值)反求它对应的分布函数。即寻找一个特殊的分布函数 [离散变量时指一串数n1,n2…,连续变量时指密度分布函数g(x)或者相对密度分布函数f(x)--它就是概率语言中的概率密度分布函数],使它计算出来的复杂程度C
(泛函数)恰好是最大(极大)的。显然这是一个已经知道泛函数(复杂程度)取极值(最大)求未知函数的问题。解这个问题的基本思路与求函数极值类似,所以在介绍求泛函数极值之前,下面先复习求函数极值的一般思路。
§12.3 求极值的一般思路
寻找极值的问题很普遍。一年的温度是冬冷夏热,如果以横坐标为日期,纵坐标为温度,我们就得到一个温度年变化的曲线。我们用眼睛很容易发现温度最高的是那一天。这是用眼睛寻找最大值的方法。在这个例子中的极大值(温度最高)实际是一个“点”(日期)。
中学数学里介绍一个一元函数,如y=f(x),的极值问题,它就是上面问题的抽象化。微分知识给出了求连续函数极值的一般方法,其基本步骤是:
这些知识一般大学数学课里都介绍。
例如 已知y=x2-x+6,问x取什么值时y达到极值?我们求y对x的微商,得
y'=2x-1
令这个微商等于零(找原函数代表的曲线的斜率为零的点),得到x=0.5。这就是极值点。因为原函数对x的二阶微商=2,它大于零,说明这是极小点。以x =0.5代入原函数,达到它的极小值5.75。这里0.5和5.75是本问题的极值位置(点)和极值的具体值。
在后面的应用中经常不大关心这个极值本身究竟是多少,而更关心在自变量是什么值时使函数值达到极值。所以有时我们就不再讨论极值究竟是多少。这类似于我们仅问今年最热的是那一天而不过问今年的最高温度具体是多少。
以上求函数极值的思路也是适用于求泛函数极值问题的。但是函数求极值问题的答案是给出函数达到极值时自变量位置(自变量的值),它是一个“点”。泛函数极值问题中极值本身也是一个值,但是与该极值对应的不是自变量的一个点(具体值)而是一个具体的函数。
对最复杂原理的一个重要应用就是求分布函数。复杂程度极大(最大)对应泛函数的极值。但是,使复杂程度极大所对应的不再是一个数而是一个函数。这个函数恰好就是我们要寻找的分布函数。所以寻找一种数学技术可以借助复杂程度最大反求分布函数就成了重要的问题。
幸好在数学中有一个重要的求泛函数极值的方法,称为拉格朗日方法。它不仅恰好满足我们的要求,而且当问题本身还要补充一些附加条件时也可以方便、统一的处理。下面就介绍这个方法。
----§12.4拉格朗日乘子法(1)----