前面的讨论都把广义集合、分布函数、复杂程度的随机性最后集中在设法计算“不同的广义集合、分布函数、复杂程度出现的概率的大小”这个问题上。现在从一个弹子球模型讨论它
(图11.1)。
图
11.1 弹子球游戏 (从右侧窄道中弹出的每个球,共10个,必然自动落入一个小穴中。
| 有m个球得100分 | m=0 |
m=1 |
m=2 |
m=3 |
m=4 |
m=5 |
m=6 |
m=7 |
m=8 |
m=9 |
m=10 |
| 10个球累积得分 | 500 |
550 |
600 |
650 |
700 |
750 |
800 |
850 |
900 |
950 |
1000 |
| 该事件出现的概率×1024 | 1 |
10 |
45 |
120 |
210 |
252 |
210 |
120 |
45 |
10 |
1 |
| 复杂程度(比特) | 0 |
4.6 |
7.2 |
8.8 |
9.7 |
10 |
9.7 |
8.8 |
7.2 |
4.6 |
0 |
表的第1行是10个球中得100 分的球的个数m 。知道了m ,也就知道了得50分的球的个数是10-m 。所以 m 值已知也就是知道了分布函数。利用游戏规定也容易计算累积得分(第2行)。第3行是根据前面的公式计算出来的概率值,在表中列出的是概率值的1024倍。而1/1024是0.5的10次方的值。
另外,根据复杂程度计算公式(7.5)还可以计算不同得分(不同的分布函数)对应的复杂程度。例如m=2对应600分,它对应的复杂程度C(2)显然应当是(两个100分,8个50分)
C(2)=-2ln(2/10)-8ln(8/10)
C(2)=5.003
以ln2除它就得到以比特表示的复杂程度的值7.2比特(m=2)。我们把m 是不同值时的复杂程度都计算出来统一列在表的最后一行中。
分析这个表可以得到下面的认识
| 有随机性的广义集合出现各种分布函数都有可能,但是它们所对应的出现概率却差别很大。出现5个100分5个50分的情况最多。它对应的概率是252/1024,即25%。 | |
| 得1000分的事件的出现概率是1/1024,或者说1000次游戏勉强遇上一次。这保证了庄主不赔钱,而游戏者,平均地说,玩1000次才接近得一次重奖。 | |
| 分析概率的数值与复杂程度的数值的关系可以看到高概率对应的复杂程度也大。概率最高则复杂程度也最大。 |
这个例子说明有随机性的广义集合,在一些场合其不同的分布函数的出现概率是可以计算的。而且其对应的复杂程度也可以计算出来。
我们特别关心不同的广义集合的出现概率与它的复杂程度的关系,如果以概率取对数为横坐标,以复杂程度为纵坐标,我们得到图11.2。从中可以看到复杂程度与概率的对数是良好的线性关系(直线)。
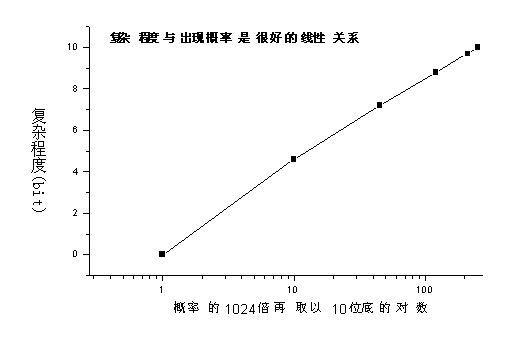
通过讨论和这一张图,我们得到了这样一个认识:本模型显示,对于有随机性的广义集合,在一次实现中具体出现那一种广义集合都有可能,但是出现概率高的广义集合恰好是复杂程度也高的广义集合。