第一推动的非演化性与演化科学概述(
2)![]()
欧阳首承1 彭涛涌2 王 忠1 林 益3
1成都信息工程学院, 610041 (中国.成都)
2
广东省气象局,510080(中国.广州 )3
Dept. of Mathemaics, Slippery Rock University.pennsylvania (USA)2002,02公布于 http://entropy.com.cn
3. 非线性与物理空间转换
非线性是数学名词,表现为数学方程式中未知函数的非一次项。若函数为非小数的有效数量时(若为小数有效值,可因其乘积成为无效小数值的误差运算,即为Chaos学说存在的原则性问题),其数量变化可呈指数形式爆发性增长,比线性更加不稳定,并可较快的演变为数量的无界性。这里以简单的微分方程为例作一说明。
3.1 欧拉语制的微分方程
此方程的定解问题可以写为
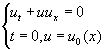
![]() (3.1)
(3.1)
即使由传统方法,也不难求得其解为
![]() (3.2)
(3.2)
或
![]() (3.3)
(3.3)
式中,![]() 为初值散度。将(3.2)在
为初值散度。将(3.2)在
![]() < 0(辐合)时绘制成图3.1,由图中可以看
< 0(辐合)时绘制成图3.1,由图中可以看
到非对称的物理空间转换。这表明非线性问题(3.1)含有,
当![]() <0时,可由
<0时,可由
![]() < 0转换为
< 0转换为
![]() > 0 ,并又是非对称的;
> 0 ,并又是非对称的;
而在
![]() > 0时,当t
→ ∞,
> 0时,当t
→ ∞,![]() →
0。相应的
→
0。相应的 ![]() 不能等
不能等
于0
,因为![]() =0
,(3.1)问题为平凡解。所以是非对称的,也是不可逆的,不能构成可恢复性变化,而成为演化问题,并在t=tb时,构成了转折性变化。即在有限时间内(3.1)问题的初值体系就可崩溃消亡,而在t稍大于tb时就已由辐合转换为辐散的非初值了。
=0
,(3.1)问题为平凡解。所以是非对称的,也是不可逆的,不能构成可恢复性变化,而成为演化问题,并在t=tb时,构成了转折性变化。即在有限时间内(3.1)问题的初值体系就可崩溃消亡,而在t稍大于tb时就已由辐合转换为辐散的非初值了。
此例非常简单,但已足以说明非线性问题与线性问题有本质性差别:
1) 非线性问题在有限时间内不能满足物理量守恒,
在
的左右是非对称的。
2) 非线性问题可在有限时间内(
)出现数量的无界性。由上一节讨论知数量无界性是物理空间的转换。
3) 数量的无界性不等于不确定性, 而 是遇到物理空间转换时数量不能以确切 的数值描述而已。也可以说转折问题不 是数量问题,即非线性问题涉及了物理系统的空间转换。此例说明了初值的辐合可在(
)时刻,转换为辐散而称为溃变(blown-up)。为此,数量的无界性,恰恰是物理结构转化的确定性。这也顺便说明了物理的确定性,并不是牛顿的初植确定性问题,而应是含转折性变化在内在的演化确定性,初值不变性不是演化。
3.2
拉格郎日语制的微分方程 作为讨论问题的直接性,不妨以牛顿第二定律为基础,由动力系统的数量数学模型,有(3.4)式的左端若乘以m,即为牛顿第二定律。式中u为运动变量(速度),t为数量时间,F为“物、力”分离体系的作用力,以数量表示。(3.4)式也称为数学模型的拉格郎日语制动力系统的一般形式。
显然,作为一般性,F可以是u的不同形式的函数。例如,若F是u的不同次数的多项式,即可讨论二次或三次式等非线性特征,并可以证明涉及非线性演化溃变的八个定理[7]。这里仅給出二次式的情况。取二次式的一般形式,
![]()
式中p,q为常数。由(3.5),(3.4)可以写为
显然,若p,q为不同值时,(3.6)具有不同形式的解,可分为三种情况:
1)![]()
![]()
上式积分后,有
![]()
式中A0为常数。由(3.8)知,若A0 > 0,则u连续变化,不出现转折性的溃变。应说明的是溃变不同于台阶式的跳跃性突变,而是完全不同于初值体系的转折性变化,溃变不只是数量增、减,而是性质或形态结构的变化。
2
)![]()
上式积分之,有
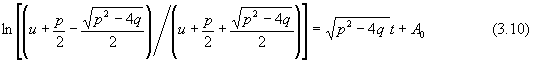
由(3.10)知,若运动限于![]() 的有界的局部变化时,则
的有界的局部变化时,则
![]()
(3.11)
所描述的光滑解仅仅是有限的局部情况。有趣的是(3.11)微商一次,即可得到困扰人们长达一个多世纪的孤立波解。或者说著名的孤立波问题仅仅是二次式非线形模型的特殊情况,不具普遍性。若![]() ,即对于整体普遍性,有
,即对于整体普遍性,有
![]()
即(3.12)揭示了运动可演化为转折性的溃变,并当A0
> 0,溃变将发生在![]() 。
。
3
)![]()
积分上式,有
![]()
取![]() (n=整数),则(3.14)描述了周期性的多次溃变(b1own-ups)。
(n=整数),则(3.14)描述了周期性的多次溃变(b1own-ups)。
![]() (4.2)
(4.2)
必然没有涉及演化,仅体现了第一推动下常加速运动,即牛顿第二定律没有体现变加速或旋转,也可以说变加速和旋转已经不是惯性系的第一推动了。
考虑到实际物质的结构非均匀性,正如老子指出的“道之为物,其中有象”[8]。也可以说成“天下无非象之道,物生而有象,象成方有数”,和墨子的“力,形之所以奋也”[9],则(4.2)式可以改写为
![]() (4.3)
(4.3)
r
为密度,即单位体积的质量;-Ñ S为物质非均匀的梯度力,若S为均匀的常数则-Ñ S=0,当物质是均匀的质点时是没有力的,即“上帝”也必须是有结构的。有趣的是,早在2000多年前中国的墨子已经解决了力是什么,但近代科学还在乞求上帝。显然,若r 、S即使作为数量的变数,(4.3)也是数学的非线性问题。由前面的讨论知,(4.3)应含有较为广泛的演化的溃变,并更有意义的是,即使在惯性系的稳定下,十九世纪末(1898)已由皮雅克涅斯证明了环流定理,即(4.3)式右端为
![]() (4.4)
(4.4)
或称为涡源的非线性力管项[10]。这表明对于实际的非均匀物质,已经不是第一推动,而是相互作用的第二搅动,之所以称为第二,其原因是在于物质非均匀结构是第一位的,而力、数量等都是物质的属性,故为第二位。重要的是搅动必然导致旋转,而旋转不是单一的,必有内旋、外旋共存,否则仅为内旋或外旋都不能独立存在。这正好是自然界对立统一原理的由来,并较早地体现于中国古代的“阴、阳”中。
作为近代自然科学,环流定理是应当有其独到的贡献的,但并未为现代自然科学所广泛和深入的理解。因为它隐含了相互作用的非线性已经体现了物质结构的含义。当年皮雅克涅斯已由此指出了大气、海洋都是以涡旋运动为基本特征的。现在已发现地壳的板快不仅是旋转的,并地壳应力集中的“构造结”,也是由于旋转才导致能量集聚的[11];地震也发生于应力轴的旋转[12]。由此,也说明了实际的宇宙物质采取旋转运动方式,似乎应当是非常清楚的问题了,并已构成对经典力学的重大叛离。