用译码模型解释颜色视觉

英文原文：https://researchfeatures.com/explaining-colour-vision-decoding-model/

摘要：虽然颜色技术有了很大发展，人眼从物理颜色到心理颜色的转换机制仍然不很清楚。为此，我于多年前提出译码模型。和比较流行的阶段模型比较，译码模型能更加直观地解释色觉进化，色盲和互补处理；并且它能用于电脑图像的颜色转换。

颜色感觉一直是科学界感兴趣的话题。尽管颜色技术有了很大发展，转换物理颜色到心理颜色的色觉机制仍然不够清楚。解决这一疑难问题将能帮助我们理解色觉，有利于有关工业——涉及材料（纺织，塑料等）、照明和彩色制图。

广泛接受的颜色视觉理论是：颜色信号在视锥细胞（视网膜中的色光敏感细胞）阶段以三色素形式存在【1,2】，而在视神经（连接神经节细胞和脑皮层）阶段以互补色形式存在【3】。支持这个理论的数学模型被称为阶段模型(Zone Model)【4,5】。阶段模型存在已经超过半个世纪，存在不同版本。不幸的是，它们虽有改进，但是仍然不能解释为什么颜色信号以这种方式处理。并且，用它们并不能解释色觉进化，也不便解释色盲。已有的两个阶段模型见图1

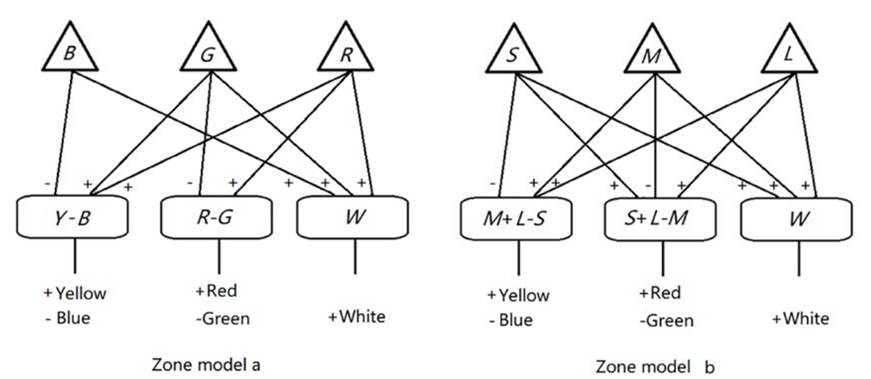
图1. 两种阶段模型用不同方式得到成对信号+red/-green（+红/-绿）。但是两者都使用颜色分量的加法得到黄色信号：R+G=Y（红加绿等于黄）或M+L=Y（中波+长波=黄）。

为了在这一知识缺口搭起桥梁，我于上世纪80年代提出色觉译码模型【6-8】——阶段模型的一个新版本。我们能用这一模型解释色觉进化和色盲【9】.这一研究引导了我后来的语义信息论和科学哲学研究【10-12】。

色觉的经典理论

色觉机制的经典理论（包括阶段模型）建立在托马斯.扬（Thomas Yound）和赫尔曼.冯.赫尔姆霍茨（Hermann von Helmholtz）的三原色理论和爱华德.黑林(Ewald Herring)的互补色理论基础上。三原色理论肯定视锥细胞接收红绿蓝三色信号【2】，人脑把它们翻译成许多心理颜色信号。这一理论特别适合计算机绘图。而互补色理论主张视网膜产生三对心理颜色信号（红绿，蓝黄，黑白）【3】，它能更好解释负后像现象——比如，你注视白墙上红色圆形20秒后，再看全白的墙，就会感觉白墙上有一个绿色圆形（其实是青色圆形；互补色理论中红绿其实是介于红青和绿绛之间的一对颜色）。参看图1：

图2 红色的互补色其实是青色

结合上述两种理论的阶段模型（见图1）【4-5】已被广泛接受。在阶段模型中，短波、中波和长波信号构成的矢量（S,M,L），或蓝、绿、红信号构成的矢量（B,G,R）代表一种颜色。这些模型描述：颜色信号在视锥阶段以三色素形式存在，而在视神经阶段（从视网膜输出时）以互补对形式存在。

流行的阶段模型存在的问题

流行的阶段模型的问题是：怎样转换（B,G,R）或（S,M,L）到三对互补色，进一步到心理颜色？心理色可用色调H、饱和度r和明度表示L。到目前为止，阶段模型已有很多版本，但是没有一个能用于计算机绘图需要的颜色转换（绘图时要把心理色转换成三原色，预测效果或计算色差时要把三原色转换成心理色）。

我认为，之所以存在上述问题是因为：用流行的模型，即使我们加上很多系数，我们还是得不到一个圆柱形颜色空间（角度表示色调，半径表示饱和度，纵坐标表示明度）。我认为，颜色加法成立实际上是颜色矢量相加成立，而不是分量相加成立。上述模型使用分量相加，由红加绿得到黄（即R+G=Y，或S+M=Y）是不对的！我们应该用颜色矢量加法：(0,0,R)+(0,G,0)=(0,G,R), (0,G,R)包含黄但是未必显示黄。比如(0,0.5,1)=0.5(0,1,1)+0.5(0,0,1)包含0.5份黄和0.5份红，等于1份橘黄。而不是G+R=1.5份黄。我因此提出，我们需要三对彩色互补色而不是两对。

译码模型

译码模型（参看图3）是一个对称的色觉机制模型，它统一三色素说和互补色说更加自然。

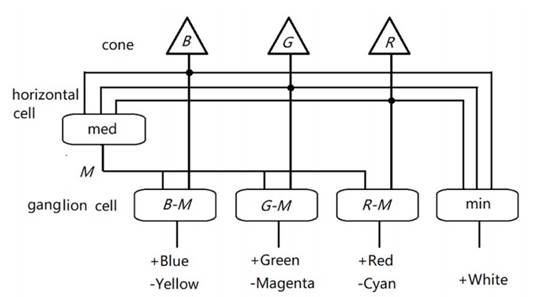
图3. 色觉机制译码模型。首先得到中间值M，再分别用R,G,B减去M得到三对互补色信号。

译码模型使用兼容布尔代数的模拟逻辑或模糊逻辑运算，它把色觉机制解释为模糊3-8译码器——类似于电子电路中选址（8中选1）用的3-8译码器。和使用算术运算的阶段模型不同，译码模型是对称的。转换物理颜色到心理颜色时，用流行的阶段模型需要很多系数，而用译码模型不需要任何系数。译码模型能更直观解释色觉进化和色盲，并且能用于计算机绘图需要的颜色转换。

解释色觉进化

用译码模型，我们可以通过分裂色敏感曲线解释色觉进化（参看图4）。

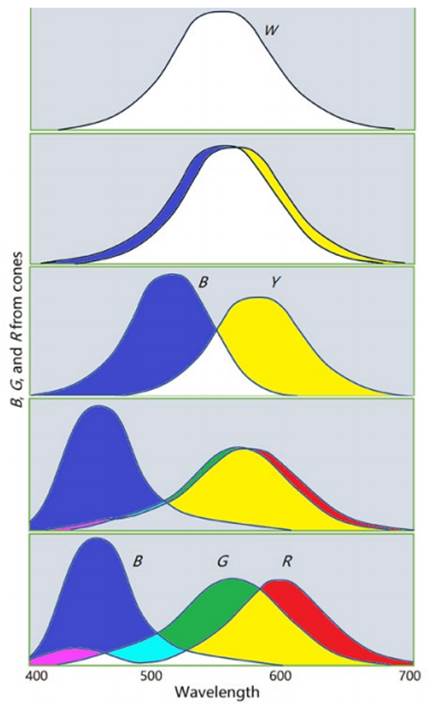
图4. 色觉进化图解

如果G和R曲线逐渐合并变成Y曲线，红、绿、青、绛四色就逐渐消失。然后，如果B和Y曲线再逐渐合并，就剩下黑白区域。我们可以想象人眼色觉机制通过相反的方式进化，人眼开始只有一种敏感细胞，只能看到黑白二色；后来敏感细胞分裂成两种，人眼也能看到蓝黄二色。再后来，两种色敏感曲线分裂成三种，人眼就能看到八种颜色，

解释色盲

根据译码模型，我们可以通过三敏感曲线的不完全分裂来解释色盲（参看图5）。

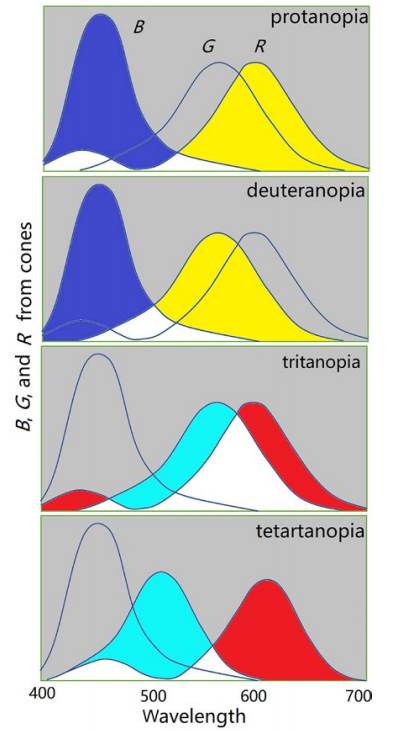
图5. 色盲图解

单色（只有黑白感觉）感官可用蓝、绿、红三敏感曲线没有分裂开来解释。红绿色盲可以通过假设G-曲线和R-曲线没有分开来解释。它们可以分为红色盲和绿色盲只是因为敏感曲线峰值偏左或偏右。蓝色盲（或蓝黄色盲或第三色盲Tritanopia）很难区分蓝和绿，紫和红，黄和绛。译码模型解释：这是因为B曲线没有从G曲线分裂开来。第四色盲和第三色盲类似，但是不易看出黄色（黄色感觉接近黑色），这是因为红青两种色敏感细胞分得较开。

解释互补处理

我用和布尔代数兼容的模糊逻辑解释互补处理。使用译码模型，我们首先得到B、G、R中间一个M（M=BGꓦGRꓦGR），然后分别用B、G、R减去M得到三对互补色信号大小（参看图3和图6）。该互补处理可使五种色觉单独出现（绛色不是单色光，有些例外）。

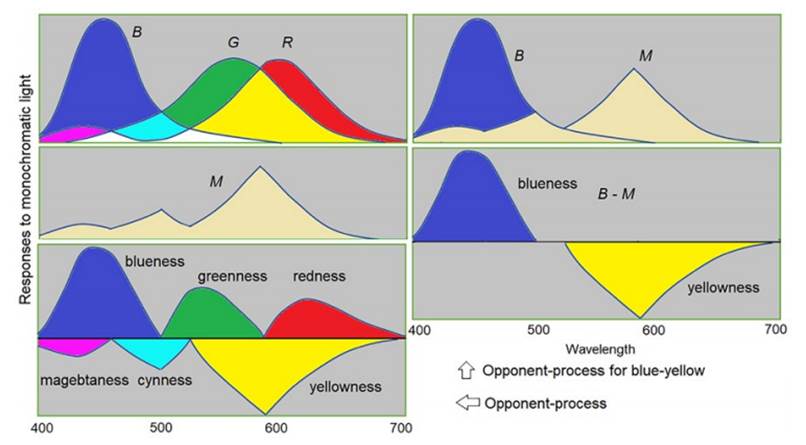
图6. 互补处理：反应色觉的处理结果随单色光波长变化

和其他对称颜色模型比较

我提出译码模型之后，发现计算机专家Alvy Ray Smith的计算机绘图颜色转换模型【15】。我们使用了相同互补处理和转换公式——从物理色转换到心理色。我解释：使用逻辑运算，我们可以把颜色矢量（B,G,R）分解成位于图7圆周上的两个相邻的单纯色和中间白色的线性组合。用这三个颜色（位于一个扇形三个顶点）的分量，我们就能用加权运算能得到色调、饱和度和明度。

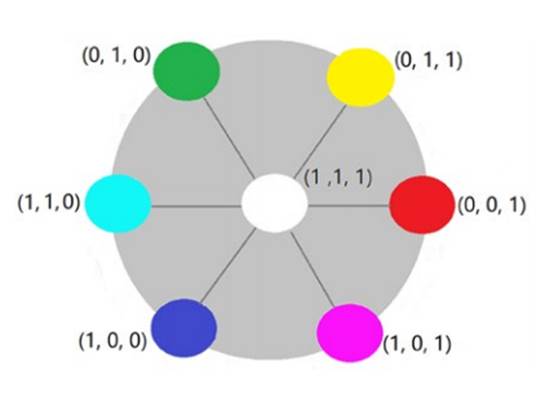
图7. 颜色分解圆盘。三个分量必然落在一个扇形的三个顶点上，用这三个分量就能得到色调、饱和度和明度。

我的研究和Smith先生的研究的区别是：

· 译码模型是色觉机制模型，其中B,G,R是三刺激值，从色光到B,G,R存在非线性转换【7】，而Smith的模型是颜色转换模型，其中B,G,R是一个像素三个发光元件受到的三刺激值，没有非线性转换环节。

· 我用模拟逻辑运算和译码器解释颜色的生理转换，而Smith没有译码和模拟逻辑运算解释，他用if-then语句做运算。

· 我通过德摩根公式证明了互补处理的结果是三对彩色信号，而Smith没有证明。

· 用译码模型能直观图解色觉进化、色盲和互补处理。

更广的意义

国际照明协会CIE于本世纪初提出一个兼容Smith模型和译码模型的对称色觉模型【16】，同样使用了图7所示色轮。用译码模型就可以统一国际照明协会的颜色对称模型和Smith的颜色模型。结合现存的模型和方法，我们可以得到更好的转换公式——在准确的三刺激值、电脑颜色（B,G,R）和心理色（色调、饱和度、明度）之间的转换。

参考文献

[1] Young, T. (1802). Bakerian Lecture: On the Theory of Light and Colours. Phil. Trans. R. Soc. Lond, 92, 12–48.

[2] Young–Helmholtz theory, https://en.wikipedia.org/wiki/Young%E2%80%93Helmholtz_theory

[3] Solomon, R.L., Corbit, J.D. (1974). An Opponent-Process Theory of Motivation: I. Temporal Dynamics of Affect. Psychological Review, 81(2), 119–145.

[4] Walraven, P. L.: On the Bezold-Brucke phenomenon. J. Optical Society of America 51(10), 1113-1116 (1961).

[5] Fairchild, M.D. (2013). Color Appearance Models (3rd Edition), John Wiley & Sons. Available at: https://last.hit.bme.hu/download/firtha/video/Colorimetry/Fairchild_M._Color_appearance_models__2005.pdf [Accessed 11th March 2021].

[6] 鲁晨光. (1986). 色觉新说和机制模拟. 心理学动态, 14(2), 36-45.

[7] 鲁晨光，(1989)，色觉的译码模型及其验证，光学学报, 9(2), 158-163.

[8] 鲁晨光. (2000). 译码模型:一个对称的色觉模型，http://www.survivor99.com/lcg/my/colormodel.htm

[9] 鲁晨光. (2020). Explaining Color Evolution, Color Blindness, and Color Recognition by the Decoding Model of Color Vision. In: Shi Z., Vadera S., Chang E. (eds). Intelligent Information Processing X. IIP 2020. IFIP Advances in Information and Communication Technology, 581. Springer, Cham. Available at: https://doi.org/10.1007/978-3-030- 46931-3_27

[10] 鲁晨光，《广义信息论》，中国科大出版社，1993。

[11] 鲁晨光，《色觉奥妙和哲学基本问题》，中国科大出版社，1993.

[12] 鲁晨光， (2019). Semantic information G theory and logical Bayesian inference for machine learning. Information（语义信息G理论和逻辑贝叶斯推理用于机器学习）, 10(8), 261. http://www.survivor99.com/lcg/cm/gtheory/index.html

[13] 鲁晨光，Channels’ Confirmation and Predictions’ Confirmation:from the Medical Test to the Raven Paradox（信道确证和预测确证——从医学检验到乌鸦悖论），http://www.survivor99.com/LCG/CM/Raven/index.html

[14] 鲁晨光，The P–T Probability Framework for Semantic Communication, Falsification, Confirmation, and Bayesian Reasoning（P-T概率框架用于语义通信，证伪，确证和贝叶斯推理），http://www.survivor99.com/LCG/CM/P-T/index.html

[15] Smith, A.R. (1978). Color Gamut Transform Pairs. Computer Graphics, 12(3), 12-19. Available at: https://doi.org/10.1145/800248.807361 [Accessed 11th March 2021].

[16] CIELAB. (2006). Symmetric colour vision model. CIELAB and Colour Information Technology. Available at: http://130.149.60.45/~farbmetrik/A/FI06E.PDF [Accessed 11th March 2021].

关于颜色的数学和哲学的更多讨论，见：我主页http://www.survivor99.com/