一条贯通热力学和动力学的桥梁b

一条贯通热力学和动力学的桥梁b

吴力航（奥地利）

2004年9月公布于潜科学网站

4．由J模型产生的认识观

4-1．J模型对狭义相对论的一点补充　　　　　　　　　　　　　　　　　　　　

由第3节J轴的引入过程易于明了，从物理量纲、刻度、以及时空属性上看，J轴与普通速度轴毫无不同。因此原来在普通速度轴上的一切自然规律在J轴上的函数形式仍然不变，最多只是因静止点的定位不同只有数值上的差别。J轴所做了的只是将普通速度轴上的静止点平移了一下，由一个表示相对静止的静止点移动到了具有绝对性意义的、表现了物质共同自然本性的物质状态点上。但就是这一点移动，使得我们在无数个等价的、仅具运动学意义的参考系中找到了一个唯一具有双重意义的参考系，它同时既具有运动学意义又直接与物质的微观结构始终联系着。因而它是一个具有绝对性意义的唯一参考系，其它一切参考系都是仅具相对意义的参考系。具有这样一种特点的参考系可能正是爱因斯坦曾经梦寐以求的。

另外，绝对速度J的建立扩大了速度的物理含义，我们将不再是象以往那样仅从纯粹的运动学角度去看待所谓的静止问题和运动问题，而是从更深入和更广泛的意义上来看待宏观运动与物质性质之间的深刻联系。因此，这里的绝对静止不仅仅指运动学意义上的静止，更是代表着对物质状态的一种认定。无论仅仅表现运动学意义上的绝对静止的以太系是否已被试验证实了它的存在，这种由J模型指出了的、表达了物质形态意义上的绝对静止都是必定存在并且有着物理实在意义的。一切运动学和热力学事件都应该可以被包含在由绝对速度轴J指定的范畴之内。

在只有普通速度轴的当今理论体系中，实际上几乎一切热力学事件都被禁锢在了普通速度轴的宏观静止点A点上，无法向着A点以外的区域中伸展，那些A点以外的速度区域，只是“纯净的”动力学的固有领地。但应该清醒的是，普通速度轴只不过是人们用来观察物质世界的一个带片面性的工具。它就象用平面的照像手段去试图反映三维的实物形状一样，结果对三维情况的了解被无情地限制在了只能想象的思维范畴内而根本无法对它进行直接的实际测量。因此，站在普通速度轴上，热力学问题和动力学问题永远只能是部分相交的两大物理事件，它们是不可能从实用技术层面上全面贯通的。J轴使得我们转换了一个角度来看问题，原来被普通速度轴投影成了一个点的全部热力学事件，也将全部展开在整个速度轴上。使得热力学在同样作为描述运动和能量关系的理论的意义上与动力学统一了起来。可以想象，利用这个新的工具，将会产生出一大批现在还无法实现甚至无法想象的实用技术来。

由一个相对性的参考系去观察其它的参考系，这就是狭义相对论的认识特点，也是它否定了以太参考系后的必定结果。但是，它在成功地打破了相对以太静止的参考系的优越地位的同时，却又使自己陷入了新的困境中━━无法使自己从那种相对性中脱离出来，而必须保留惯性系的优越地位。因为抛弃了具有绝对意义的静止点也就丧失了自然规律的一种共同参考标准，相对论只好借助惯性系来作为一种无可奈何的“新型”的共同参考标准。所以说它的时空观是一种相对的相对时空观。我们不得不悲观地承认，“保留惯性系优越地位”这一理论缺陷，在不突破普通速度轴范畴的前提下，是不可能由狭义相对论以自我完善的方式来自行解决的。同时，仅限于从运动学意义上着眼，试图去寻找运动学意义上的真实的绝对静止参考系，其努力恐怕也会是徒劳的，至少在目前是十分困难的。

现在，情况有了改观，J轴的获得使得狭义相对论有可能实现自我完善了。相对论原理实际上告诉了我们，由某一个惯性系中得出的自然规律其函数形式是广泛适用的，在跨越不同时空所体现出来的不同只是关于时空的基本度量值。简而言之，相对论对经典力学理论所作的最大贡献，就是把迦利略、牛顿绝对时空观中的速度v用相对论时空观的速度u进行了一个代换，原有的函数形式保持不变。同理，将任何经典理论中的用绝对速度J进行代换，就使得原来运行于普通速度轴上的自然规律转而在J轴上运行了。表面看来用J的代换与相对论所作的u代换无甚不同，其实这里有着一个质的变化。首先，它把一切关系到运动和能量的自然规律都放到了一个共同且唯一的参照零点上来了，这就象用绝对温标对摄氏温标改造的意义一样。其次，它由此还带来了一个新的、在狭义相对论方法中所没有的解决问题的新线索：由于J与物质结构的紧密相关性，使得J值直接与在过程的进行中系统向环境吞吐的能量联系起来了（见4-3.节）。由此，除了用速度变换法则这种数学手段来了解不同时空之间的差别之外，还多了一条以实际测量为依据的途径━━可以通过考察系统与环境之间的能量吞吐情况来了解某个系统在跨越不同时空时发生的改变。只要确定了某系统在经历某个过程(无论是热力学过程还是动力学过程)时的J值的改变量(这个改变量是基于我们所处的观察系得到的实际测量值)，就无须再借助一个另外的速度u，而是直接揭示出物质状态的改变情况。同时也就意味着它已经包含了狭义相对论直至广义相对论的变换内涵。狭义相对论必须保留惯性系优越地位的缺陷被J轴模型以极自然的方式消除掉了！显然，这里是采用了与爱因斯坦不同的途径━━建立合理的静止参照点来消除的。也就是说，重新找到的绝对静止点，使得我们可以不再依赖惯性系来作为自然规律的共同参考标准了。

惯性系优越地位的消除也就极自然地消除了狭义相对论的第二个内在缺陷━━“无法自然地描述引力。”由于引力是属于加速度运动范畴的自然现象，因此，建立在讨论匀速运动基础上的狭义相对论对它无法讨论。而J轴是一条再自然不过的速度轴，用它来讨论问题丝毫不会受到是匀速还是匀加速甚至变加速的限制，也就是说无须受到必须建立惯性系的制约。在此，引力只不过是由牛顿第二定律的J形式 F=(dJ/dt)m 所描述的一个力而已，与一切基于惯性质量和加速度运动的力学力并无本质上的不同。所谓加速场与引力场等价、惯性质量与引力质量相等也就是自然而然的事情了。通过后面几篇专门讨论引力问题的文章将会更加明了，加速度运动产生的力学力和万有引力其实只不过是同一个J的加速度场dJ/dt的两个表现方面而已，它们的力学属性相同。在J模型的意义下，引力和力学力（弹力）都可以用牛顿第二定律来描述，它们本质上都是使物体产生了dJ/dt的加速度（结构变化）。惯性质量和引力质量当然是相等并同质的，所不同的只是产生引力和产生弹力的具体物质结构运动方式不同罢了。用J的语言来说就是：产生于物体内部全体积范围的、均匀的dJ/dt的力为弹力；产生于非均匀的、局部区域的结构涨落方式的dJ/dt的力为引力。

J模型使我们站到了一个绝对意义的参考系上，因此在J轴上运行的相对论就具有了绝对性的意义。它是由一个具有物理实在意义的绝对静止点去看世界的，与迦利略、牛顿仅从运动学意义上定义的绝对时空观有着本质的区别，但又具有着相同的特征。由这个绝对静止的参照点去描述自然规律将会具有更加真实和简洁的结果。可以说运行于J轴上的相对论是一种具有绝对性意义的相对论。这样，我们由迦利略、牛顿的狭义绝对时空观，经过了爱因斯坦的相对时空观，进入到了更新层次的广义绝对时空观。由J模型对自然规律进行的描述就自然地抹平了由狭义相对论和广义相对论联结所带来的生硬感觉。我们看到，对普通速度轴上静止端点的那个小小的一移有可能消除掉狭义相对论百年来的困惑。

综上所述，可以归纳对比一下经典理论时空观、相对论时空观、J模型时空观之间的关系和区别。用字母v、u、J分别表示与经典理论、相对论、J模型所对应的速度轴，则可以说，仅就速度轴的刻度而言，这三条速度轴完全相同。它们三者之间的关系则是以相对论速度变换法则相联系的。它们三者在认识观意义上的差别除了在关于速度轴的高速端（真空中的光速）的认识方面外，更为重要的是在关于静止点的认识上。v轴的静止点是不真实的绝对静止点(其实它是个相对静止点，或者说只是纯运动学意义下的静止点)；u轴的静止点是惯性系中的相对静止点；J轴的静止点是表现了万物同一的物质状态的绝对静止点。J轴是一条由起点到终点、与物质世界中的一切物质形态完全一一对应的、具有物理实在意义的闭合区域。它的两个端点代表了物质的两种极限状态━━理想气体和理想晶体。由以上对比，不难看出由经典理论到相对论再到J模型理论的认识特征。

另外，不难发现，在我们早已熟悉的那条普通速度轴上，存在着这样一个现象：几乎一切实际的物理事件不是聚集在紧靠“静止”的一端就是聚集在紧靠近光速的一端。似乎那是一条中间地段为一片荒漠，极难捕捉到具有物理实在事件的速度轴！这种“中间速度空缺”的现像总会让人不由自主地产生出一种不安：难道上帝确实忘记了对物质世界作一种更加符合逻辑的安排、给我们提供一条均匀密实的速度轴了吗？现在，我们看到，其实当自然界中的一切物质在J轴上重新分布开来以后，所形成的将是一条均匀密实的速度轴。因为自然界中的物质，从物质形态上讲，应该是一条从理想气体到理想晶体之间的任何一种中间状态都确实存在的、真实的物质链。在J轴上，“中间速度空缺”的荒漠被消除掉了！

4-2．J模型将使得相对论科学原理直接进入到日常应用技术领域中来

狭义相对论在J轴上的运用将使得运动和静止、热力学和动力学获得统一。这是因为自然界中的任何能量形式最终都可归结到不是属于热量就是属于功这两个最基本的能量形式上来，而在热功当量定律和能量守恒定律的意义下，能量的变化又可归结到系统的结构改变、即J值的改变量上来。对系统施加动力学功W和热量Q都可以引起系统J值变化，它们最终将在系统与环境交换的能量相同、获得的J值的移动量就相同的意义下等量地统一起来。而热量和功的不同属性将表现为使得物体J值的移动方向刚好相反。

这种统一应该会产生出大量的新的技术方法并对已有的一些技术方法提出修正意见，以及对一些测试方法提出新的物理判据。它将使得热力学理论和热力学技术方法广泛地应用于所谓的纯动力学问题，对动力学范畴内的不可逆现象和过程提出解释和判据，为我们利用那些现在还不大为人们所注重的自然现象去开发出新的应用技术指出方向。例如，自由落体运动显然是一个不可逆过程，并且按通常的认识是一个“纯”动力学过程。但是，在动力学范畴内的一切认识和理论计算都无法对这种不可逆性提出判据。热力学也对这种“纯”动力学过程束手无策。J模型则为我们带来了新的认识，使我们产生分析和判断：这是一个受到最小熵产生原理支配的线性非平衡区中的热力学不可逆过程。在本人后面的几篇文章中将会看到，这个热力学性质与另外一个由笔者提出的、可称之为局域量频率增大效应的热力学性质的巧妙结合和运用，将会使我们获得全新的认识观和有可能开发出十分神奇的关于改造物体的重力性质的应用技术来。

从另一方面来看，动力学的理论和技术方法也将直接进入到热力学的领域。例如，目前的经典热力学理论仅能对一个不可逆过程的不可逆程度进行总的笼统的判断和估算，至于能量是以何种具体的规律和方式在过程中损耗掉的无法了解。利用J模型将有可能建立起关于热力学不可逆过程的动力学模型，并以此来分析、计算过程中的损耗功，使我们获得关于不可逆性的具体印象和定量的数据，从而优化对过程的设计和控制。　

根据J模型的物理意义易知，它在应用上的最大意义就在于使得相对论所揭示的“相对论效应”可以在“日常速度”范畴中表现出来了。在普通速度轴上，按人们一贯以来的认为，只有对于象电磁波、电子等高能粒子这一类微观运动的场合，由于它们的运动速度接近光速，才能明显地表现出相对论效应来。而在日常速度范畴里，是感受不到相对论效应的。但是，由J轴上来看则是另一幅情景了。由于宏观静止着的一个固体物体实际上已经具有了接近光速的J0值了，所以使该物体发生具有任何宏观运动速度的常规运动，在J轴上来看已不再是经验告诉我们的“速度是线性增减变化着的”，而是“J是以近光速端的非线性方式变化的”。线性变化的日常速度u映射到J轴上以后变成了非线性的绝对速度J的变化。一种“眼光”上的变换使得我们可以看到相对论效应其实每时每刻都在我们的身边发生着，并支配着我们的日常活动。

4-3．J模型的能量━━时空观

速度是一个由时间、空间参量组合成的因子，在动力学中它起着标定物体（系统）能量状态的作用。相对论指出，对于一个速度u就对应了一个时空，也就对应了一个确定的能量状态。由J模型对速度含义的扩充易于想见，一种物质结构实际上本身就是一个时空，当然也对应了一个确定的能量状态、一个可以由热力学定义的热力学状态。因此，物体的J值与它的能量状态有着一一对应的关系。这里所说的能量是包括热量在内的广义的能量。

在关于静止物体静止能的认识上，狭义相对论为什么会得出与热力学不一致的判断呢？这是因为狭义相对论是依据“光速不可突破”这个单方面的绝对性来表述相对性的，手中并没有掌握另一个方面的依据━━关于“静止”的绝对属性。（当年，狭义相对论正是经过了一番痛苦挣扎才从静止问题的束缚中最终解脱了出来，揭示出了自然规律的相对性的。）由于光速不可突破这个绝对性是正确的，是自然界在至少我们最感兴趣的这个范畴内所必须遵循的物质共性。所以，狭义相对论指出的相对性时空规律是正确的。在严格的数学逻辑导引下必然会指出“静止”端的物质属性━━静止能的存在！或者说，狭义相对论其实告诉了我们这样一个事实：宏观静止其实并不静止！但是，狭义相对论却赋予了这个相对的静止以绝对的意义。所以，它虽然正确地认识到了“静止其实并不静止”这个事实，但却使用了一个并不应该为零的零速度值代入了相对论总能公式E=mc²那个正确的函数形式，从而得到了一个错误的“函数计算值”E0，因而产生了失实的判断。这是狭义相对论在仅有一个方向绝对性保障的条件下，却又向着另一个无绝对性保障的静止方向作出了绝对性推论时产生的失误。

在J轴上，速度轴的两端都具有绝对性保障。这种两个方向上的保障使得由J模型而产生的判断更加符合自然本性的要求。在这个意义下，绝对速度轴J和绝对温标轴T (那个也是具有两个方向的绝对性保证的、因而可以正确标定物质状态的温度轴）完全同一了。所以，J模型赋予了动力学以更严谨的、与热力学认识观完全相同的能量观，使得它们各自得出的关于能量运动的科学规律将完全可以互通使用。在J模型的认识观中，所谓牛顿动能就是物体作了某个J-J0的时空越迁后所具有的能量差。从量值上讲，与同一个物体在发生了相应的T-T0的温度越迁时向环境吞吐的热量完全相等[注]。而静止能E0就是某物体在具有J0的绝对速度时的总能量。与相对论力学认识观点不同的是，这个J0是一个与具体物质有关的量，不是常数（显然，在相对论力学中实际上是把它认作了是与物质无关的常数）。进而，由绝对静止的C点到J0点，对于任何“静止质量”不为零的物质系统，所对应的能量仍然是无穷大，仍然是一个不可知值，因而所谓静止能当然只能是一个不可算知的无穷值。这就与热力学关于内能(U)的认识观完全统一起来了。

由此可见，J模型改进了动力学问题中的静止点。指出了宏观静止本质上不过是运动速度为c的一种“运动状态”而已。因此，对于宏观静止问题(通常是热力学的领地)完全可以用动力学方法去讨论。同时，它又在热力学问题中引进了宏观运动的意义。指出了宏观运动其实只不过是具有某个J值但在宏观上静止着的物质状态而已，因此对于运动问题也就完全可以用热力学方法去讨论了。所以，J模型使得运动问题和静止问题、热力学问题和动力学问题达成了统一。作为这个统一的基础科学定律是能量守恒定律（热力学第一定律）和热功当量定律。

前面提到，绝对速度J轴与绝对温度T轴一样具有双向绝对性的保障，因此，它们都可以对物质的能量状态以及能量━━时空性质作出客观而准确的表述。显然，J轴和T轴的零点刚好是相反的，T轴的零点是J轴的光速端点。统计热力学正是利用这个物质状态点作为分子能态的零点的。因为在这一点处，所有的物质都是理想晶体，其分子能态为零。由此可见，相对论原理中的“光速不可超越”和热力学第三定律指出的“绝对零度不可达到”其实所描述的是物质的同一个自然本性。这两种认识只不过是针对“理想晶体这种极限的物质状态不可达到”这同一个物质共性而形成的两种不同的表述方法而已，它们实在是同一个自然规律。同理，真空中的光速不随惯性系的改变而变化说明绝对零度也同样与惯性系的改变无关。因为与之对应的理想晶体已经是物质的终极状态了，不可能再有变化。但是，对于绝对零度以上的任何温度，其测量值都将具有相对论效应而与惯性系有关。在此借助前面提到过的那个乘分子飞机在水分子气体团中穿行的假想例子作一个简要的叙述：当我们处于那架分子飞机上并看见周围的水分子在不断地排列成水、冰、理想晶体的变化时，如果未被特别告知，其实我们并不知道到底是我们正在相对这个气体团作相对运动呢，还是该气体团正在被环境不断地抽出着热量因而它的温度在不断地下降着呢。即，无论采用动力学手段还是热力学手段对一个物体系统实施能量的输入或输出，仅就对系统微观结构的改变而言，其作用是本质相同的，是可以直接进行定量的对比的(热功当量定律)。

另外，介质中的光速随着介质性质的不同而不同、并且恒小于真空中光速这一物理现象，由J模型来理解就变得十分简单明了。因为任何介质都已经具有了一个“速度”J0，所以在宏观静止系中去确定这个介质中的光速时，实质上是确定一个以J0速度匀速运动的运动系中的光速问题。即有

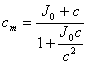
式中的cm是介质中的光速；J0是该介质宏观静止时的绝对速度；c是真空中的光速。由于J0是恒大于零的数，因此c恒小于c，并且是J0的单值函数。这种处理问题的方式就是运动问题和静止问题统一后给我们带来的便利。

上式的另一个重要的意义是，可以由它并根据对cm的试验测定来确定该介质的J0值。这样，我们有了一种可以纯粹通过试验测定来确定物质的J0值的方法，这将在J理论的实际应用中具有重要的意义。

4-4. 由J理论看“热寂说”

随着十八、十九世纪中的能量守恒定律、热功当量定律和热力学第二定律的建立，人们也曾一度为能量的守恒性和能量的衰败性(热力学第二定律)而忧心仲仲，担心总有一天宇宙中可资利用的能量(自由能)将会彻底枯竭。由J模型的认识观知，这种担心实际上是把在物质发展进程中，某一个局部阶段的表现错误地推论到了全范围所形成的误解。J模型告诉我们，物质世界是密实地分布于J轴的静止端到光速端之间的，一切与能量变化相关的物质行为都始终是沿着J轴运行的，是毫不脱轨的。在J轴的两端，都对应于能量为无穷值的物质状态，并且功和热量的差别不存在。这两个端点构成了物质的起始的源和终结的阱，永远不会因为中间状态的物质发展行为而尚失它们的功能。它们以源源不绝地运动保证着我们需要的这个中间状态的物质世界的存在。由于它们能量的无穷性，所以从整个物质形态范畴而言，能量是无法确定其具体数值的，因而言及什么能量守恒是毫无意义的。即，通常所说的能量守恒，绝不是指整个物质形态范畴而言的。

但是，由于物质的发展进程是严格地沿着J轴进行的，因此在一个局部的J值变化的阶段上，一个有限质量的物质系统只可能与有限的能量变化相对应，这时才有所谓的能量守恒的概念。这种守恒性表现为在J轴上移动的距离相等。同样，也只有在这个物质进程的中间阶段，能量才表现出了热量和功的差别，因而也才有了所谓的热力学第二定律，才出现了所谓的能量退化性问题。这种退化性就表现为在J轴上移动的方向相反。由此可见，即使是将热力学第二定律放到几何意义上的整个宇宙空间来考虑，实际上在物质状态的意义上它仍然是一个局部问题，仍然是不会出现所谓“热寂”的情况的。整个物质范畴是不存在热寂的、是一个生动活泼的世界！

在仅有普通速度轴u和绝对温度轴T的现今科学体系里，对于仅具局部意义的能量守恒定律、热功当量定律和热力学第二定律的描述，实际上采用的就只有这两条毫不相干的物质状态轴，因而无法深刻地揭示它们之间的紧密关系。宏观运动的动力学和宏观静止的热力学被这种表达方式的局限性无情地割裂开来了。J轴的建立将革命性的改变这一状况，对这种发生在物质局部进程中的行为作出统一表述。

5. 结论

狭义相对论是为了解决牛顿经典力学与麦克斯韦理论之间存在着速度无限还是有限（光速c）的矛盾发展起来的。绝对时空观和相对时空观的根本分歧是：绝对时空观认为时间和空间是绝对的，相对运动的坐标系是不等价的；相对时空观认为时间和空间是相对的，相对运动的坐标是等价的。这种限于运动学意义上的论战直到今天仍然十分激烈。其实仔细分析起来，牛顿与麦克斯韦的矛盾，严格说来，属于来自不同概念范畴的分歧，虽然表面看起来它们都是针对着“速度”这个运动学问题的分歧。牛顿力学时空观中的速度概念是运动学意义的；而麦克斯韦理论中的光速不变，实质上是物质结构有限性的反映。逻辑上合理的无限运动性和实际上有限的物质结构性构成了牛氏和麦氏的基本矛盾。相对论仍然只是直接从运动学意义上着手解决这一矛盾的。无可否认，虽然相对论仍然存在许多问题，但就仅从运动学意义上着手，去解决本质上起源不同的上述矛盾而言，采用建立相对时空观的方法可能是一种最佳的选择，这恐怕是相对论屹立百年不倒的根本原因。

本文提出的绝对速度J概念，可以说跳脱了纯运动学的限制，从物质结构的意义上着手来分析运动学问题，并使之能够有机结合起来。把无限的运动性置于了实际物质结构有限性的框架之中。换句话说就是，将逻辑上可以取无限值的速度中实际上以虚数形式存在的部分切除掉了，保留下了与实际物质属性相适应的实数的部分。J理论使得我们可以找出一条与实际物质结构直接相关、同时又具有运动学意义的绝对静止参考系。在这样的坐标系上运行的相对论，就有可能既消除牛氏与麦氏的矛盾，又同时解决牛氏理论在高速范畴中的适用性问题。

从J理论的可应用性上来看，通过改进力学中物体的物质模型和统一动力学和热力学的能量参照零点而建立起来的绝对速度轴J，使得相对论的广泛科学性有可能突破“宏观静止”的阻隔，直接进入到极为广泛的应用技术领域中来。这样，相对论将不再是仅能在极少数的极端状况下找到应用的、理论上的科学瑰宝，而将有可能成为一门适用面最为广泛的应用理论。其中最有意义的是有可能从应用技术的角度为对引力问题的研究找到一条新的途径。本人后面的几篇文章就是关于这个方面的讨论的。

[注]：在<<热力学系统与相对论>>一文中专门讨论了绝对速度J和绝对温度T之间的关系，并推导出了J与T之间的函数关系式，