超球宇宙中的星系计数

邓晓明

(十年前完成本文，投稿到《潜科学》杂志，但未被发表)

提要

本文在宙和宇超球结构基础上导出了星系计数的理想公式，给出了宇宙物质总量的概念，并分析了该式与观测的可比性。

关键词：宇宙模型、红移、星系计数

一、引言

在现有的星系计数公式中，星系的累积数是光度或红移的函数。由于宇宙整体时空的超球性质，光度和距离关系不再遵守平方反比律（这种关系只有在近距时才能近似成立），因而本文舍弃光度概念，在宙和宇的超球结构基础上，导出了以红移为原函数的星系计数的理想公式，并确立了宇宙物质总量的概念。

二、星系计数公式

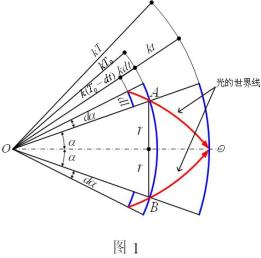
星系计数同样能够反映出我们宇宙整体结构的重要信息。见图1，设点为地球所在的时空位置；、点为某两个距地球同样远星系的时空位置。很明显，三维空间各方向上距地球为等距的所有星系（包括、两点），在宙时所发射的电磁讯号经时间后在宙时被我们收到，并且它们均匀地分布在以地球为中心的空间球面上。容易证明该空间球面的半径为：

. (1)

由于 ，，及 ，所以：

. （2）

由该空间球面所构成的空间球壳体积为：

. （3）

由图1的几何关系可知：

. （4）

由于，

所以 . （5）

将（2）及（5）式代入（3）式得空间球壳体积为：

. （6）

由天文观测可知，在观测所及的范围内，宇宙的演化早已进入了以物质为主的时期。若宇宙物质主要由非相对论性松散物质组成，并且总量守恒，我们可得宇宙物质在宙时的数密度：

. （7）

这里为宇宙物质（星系）总量；为宙时宇的体积。由 及 ，有：

. （8）

球壳内的物质（星系）数为：

. （9）

将（6）及（8）式代入（9）式得：

， （10）

对其积分得（,）范围内所有物质（星系）数总和：

（这里宙长为常数），既：

. （11）

将 代入（11）式得星系计数公式的红移形式：

. (12)

这里 是在红移[,]范围内，观测到的所有物质（星系）占宇宙物质总量的百分比。可以看出，通过测量与，我们就可以由（12）式确定宇宙物质（星系）总量.

若将 代入（12）式得其另一种形式：

. （13）

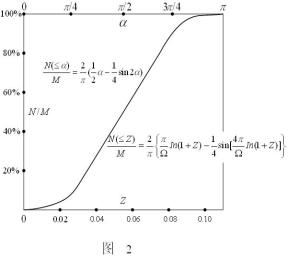
图2给出了星系计数公式的函数曲线。

若设 ，解（13）式得：. 与相对应的红移值为： (设 )。其物理意义为：当， 或 时，所观测到的物质（星系）数就是宇宙物质总量，这时我们所看到的是宇宙中全部物质的单像。相应地，当， 或 时，我们所看到的是宇宙物质总量的二重像，三重像…重像。

三、后记

由于这一公式是在理想条件下导出的，实际上任何望远镜都有一定的观测穿透极限，加之有些较远的星系有可能会被较近的掩掉，所以公式与观测可能会有些偏差；另外，当很小时，宇内同一演化物已经演化到星系状态，而当很大时，宇内同一演化物可能处在类星体状态。由于在这一演化过程中各演化物会有一定程度上的分化组合，其几何和物理性状（如尺度、形状、温度、密度等）要有一定的变异，这也会给统计工作带来一定的困难。但在一定的红移范围内，该公式可以为观测提供一个良好的参照依据。

致谢：长沙大学计算机系的鲁晨光在与北师大赵峥教授的私人通信中也曾设想过这一模型，他得到了宇宙膨胀公式这一步，但没有继续深入研究。当他看到我发表在潜科学上的第一篇论文后，写信告之上述情况并提出了许多富有建设性的建议，在此向其表示衷心的感谢。

参考文献

[1]S.温伯格，引力论和宇宙论，科学出版社，1980，P520-529

[2]刘辽，广义相对论，高等教育出版社，1987，P452-455

[3]邓晓明，1992，潜科学杂志，1，35

[4]邓晓明，1993年，潜科学杂志，（待印刷）

[5]邓晓明，1992，潜科学杂志，6，（待印刷）