泛泛系理论的圆度决定论

一、前言
促成广义集合形成的根本动力和根本规律是什么？对于这个问题，张学文先生在
<<组成论>>中有所探讨。张学文先生说[1]：“我们把‘一次随机抽样中尽管多种事件都
可能出现，但最容易出现（遇到）的事件（结局）是概率最高的事件’称为概率公理。这个公理也可以反过来表述：‘一次随机抽样中概率最高的事件是最容易出现（遇到）的事件’。”张学文先生还明显地暗示，这个“概率公理”是科学的“新皇帝”。本文旨在探讨促成广义集合形成的更为根本的动力和更加根本的规律。换句话说，本文企图解决“这个‘新皇帝’的父母亲和祖父祖母是谁？”等问题。

二、泛泛系理论的圆度决定论的完整表述
泛泛系理论的圆度决定论认为：
1) 一切事物的本原独立而不改。
2) 一切事物的本原独立而不改必然导致本来无一切指向。
3) 本来无一切指向必然产生泛泛系本然动力。
4) 泛泛系本然动力迫使事物尽量回归无一切指向。
5) 事物尽量回归无一切指向所表现出来的就是广义集合尽量服从极坐标系上的极大
圆度分布或展示所谓各向同性。
6)经科学计算与科学研究，终于确定信息熵H的数学表达式是一种比较理想的广义集
合的一般性圆度表达式。
7)当圆度最大时，广义集合就展示出极坐标系上的圆周分布、圆球面分布和超级圆
球面分布。
8 )任何条件下，圆度最大都迫使信息熵最大，张学文复杂度最大，玻尔兹曼几率最
大，分布函数发生概率最大。所以在任何约束条件下，广义集合趋向最大圆度分布这个
最大圆度定律统摄最大熵原理、最大信息量原理、最大复杂度原理、最大玻尔兹曼
几率原理、最大概率原理。

三、关于泛泛系理论的圆度决定论关键点的详细论证
3.1.  广义集合的圆度
所谓广义集合的圆度，即是表面上所观察到的各向平等度、各向同性度。圆度的实
质是广义集合的无性度以及就整体而言的无指向度。
由于各向同性分布在二维极坐标系上表现为圆周，而在三维极坐标系上显现为圆球
面；又由于各向同性有更深刻的本质，所以我们把各向同性度叫做圆度。


图一


图二

3.2. 圆度C
我从极为直观的不圆度(权重的欧几里得平方距离)出发，给出了圆度C的定义式。
不圆度 = (p1-p2)^2 +(p1-p3)^2 +...+(p1-pn)^2
+(p2-p3)^2 +(p2-p4)^2+...+(p2-pn)^2
+......
+(pn-1 - pn)^2                                           (3-2-1)

圆度C = (n-1) - 不圆度                      (3-2-2)

由此得到圆度C的一般表达式
C = n(1 -p1^2-p2^2-...-pn^2)                     (3-2-3)
=n( p1(1-p1) + p2(1-p2) +...+pn(1-pn))       (3-2-4)

对于矛 作 者: Leon 于 1/25/2007 12:01:12 PM回复

[修订稿和正式投稿稿]
泛泛系理论的圆度决定论

一、前言
促成广义集合形成的根本动力和根本规律是什么？对于这个问题，张学文先生在
<<组成论>>中有所探讨。张学文先生说[1]：“我们把‘一次随机抽样中尽管多种事件都
可能出现，但最容易出现（遇到）的事件（结局）是概率最高的事件’称为概率公理。这个公理也可以反过来表述：‘一次随机抽样中概率最高的事件是最容易出现（遇到）的事件’。” 张学文先生还明显地暗示，这个“概率公理”是科学的“新皇帝”。本文旨在探讨促成广义集合形成的更为根本的动力和更加根本的规律。换句话说，本文企图解决“这个‘新皇帝’的父母亲和祖父祖母是谁？”等问题。

二、泛泛系理论的圆度决定论的完整表述
泛泛系理论的圆度决定论认为：
1) 一切事物的本原独立而不改。
2) 一切事物的本原独立而不改必然导致本来无一切指向。
3) 本来无一切指向必然产生泛泛系本然动力。
4) 泛泛系本然动力迫使事物尽量回归无一切指向。
5) 事物尽量回归无一切指向所表现出来的就是广义集合尽量服从极坐标系上的极大
圆度分布或展示所谓各向同性。
6)经科学计算与科学研究，终于确定信息熵H的数学表达式是一种比较理想的广义集
合的一般性圆度表达式。
7)当圆度最大时，广义集合就展示出极坐标系上的圆周分布、圆球面分布和超级圆
球面分布。
8 )任何条件下，圆度最大都迫使信息熵最大，张学文复杂度最大，玻尔兹曼几率最
大，分布函数发生概率最大。所以在任何约束条件下，广义集合趋向最大圆度分布这个
最大圆度定律统摄最大熵原理、最大信息量原理、最大复杂度原理、最大玻尔兹曼
几率原理、最大概率原理。

三、关于泛泛系理论的圆度决定论关键点的详细论证
3.1.  广义集合的圆度
所谓广义集合的圆度，即是表面上所观察到的各向平等度、各向同性度。圆度的实
质是广义集合的无性度以及就整体而言的无指向度。
由于各向同性分布在二维极坐标系上表现为圆周，而在三维极坐标系上显现为圆球
面；又由于各向同性有更深刻的本质，所以我们把各向同性度叫做圆度。


图一


图二

3.2. 圆度C
我从极为直观的不圆度(权重的欧几里得平方距离)出发，给出了圆度C的定义式。
不圆度 = (p1-p2)^2 +(p1-p3)^2 +...+(p1-pn)^2
+(p2-p3)^2 +(p2-p4)^2+...+(p2-pn)^2
+......
+(pn-1 - pn)^2                                           (3-2-1)

圆度C = (n-1) - 不圆度                      (3-2-2)

由此得到圆度C的一般表达式
C = n(1 -p1^2-p2^2-...-pn^2)                     (3-2-3)
=n( p1(1-p1) + p2(1-p2) +...+pn(1-pn))       (3-2-4)

对于矛盾体而言
C = 2( p1(1-p1) + p2(1-p2))                        (3-2-5)

在(3-2-5)式中, 由于广义集合是以各向的权重为组成概率的，所以p1(1-p1) 括号左
边的p1可理解为矛盾一方的概率，它起着统计平均的作用，而(1-p1)中的p1则应该
理解为代表矛盾一方的“我”的权重。这样一来， (1-p1)就是代表矛盾 一方的
“非我”的权重。同理p2(1-p2) 括号左边的p2可理解为矛盾另一方的概率，它起着统计平均的作用，而(1-p2)中的p2则应该理解为代表矛盾另一方的“我”的权重。这样一来， (1-p2)就是代表矛盾另 一方的“非我”的权重。

所以圆度C是一个与各向的“非我权重”的统计平均值成正比的量。
我们引入平均圆度Ca：
Ca = C/n                                                   (3-2-6)
那么平均圆度就是各向的“非我权重”的统计平均值。

相比之下，所谓平均概率Pv可表达为
Pv = p1^2 +p2^2+...+pn^2
=p1(p1) +p2(p2) +...+pn(pn)                      (3-2-7)
因此平均概率Pv就是各向的“我权重”的统计平均值。

一个刻划“我”，一个刻划“非我”，显然圆度C是与平均概率Pv相对立的一种量。
这就不难理解为什么
圆度C = n( 1- 平均概率)                               (3-2- 8 )

3.3.  圆度C的物理意义
对于矛盾体而言
圆度C = 2( 1 - p1^2 -p2^2)
当矛盾双方不平等度达到最大时，p1和p2两者中一个等于0，另外一个等于1。这时
圆度C=0。另一方面，当矛盾双方平等度达到最大时，圆度C最大，等于1。当矛盾双
方的平等程度从最小变到最大时，圆度C随之单调增加，直到抵达最大值。这些可以
从下图所示的圆度C随p1的变化而变化的曲线中看出。


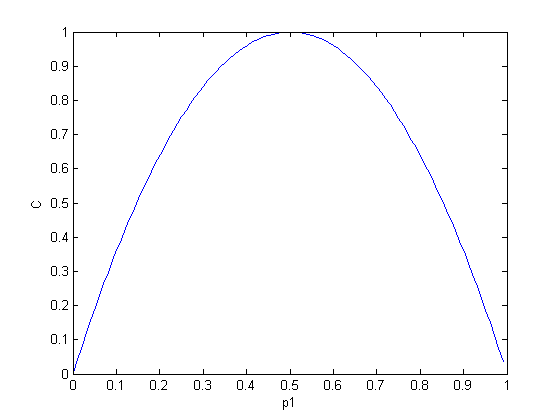
图三

由此可见，圆度C的的确确是刻划广义集合的平等程度或平等性的参数。由于平等性
又包含各向同性性，相对无我性，相对去执着性，相对去异性性，所以圆度C又是刻
划广义集合的各向同性性，相对无我性，相对去执着性，相对去异性性。
相比之下，平均概率Pv就是刻化广义集合的不平等程度，各向异性程度，相对有我
程度，相对执我程度，相对不同性度的参数。

3.4. 关于矛盾体的“圆度决定论”的严格数学证明
我所提出的所谓广义集合“圆度决定论”，就是说广义集合的最大圆度决定最大熵、
最大复杂度、最大玻尔兹曼几率、最大发生概率。
经仔细计算发现，对于矛盾体，“圆度决定论”可以严格证明。
也即是说矛盾运动中的确是最大圆度决定最大熵、最大复杂度、最大玻尔兹曼几率、
最大发生概率。

现给出矛盾运动的“圆度决定论”证明。
圆度C =2( 1-p1^2 -p2^2) =2( 1- p1^2 -(1-p1)^2)                       (3-4-1)
信息熵H = -p1log(p1) -p2log(p2)=-p1log(p1) - (1-p1)log(1-p1)      (3-4-2)
这其中p1为矛盾体一方的组成概率或权重。
因为
dC/dp1 =-4p1 +4(1-p1) = 4-8p1                                                (3-4-3)
所以，当 p1<0.5时，圆度C单调递增，而当 p1>0.5时，圆度C单调递减。在p1 =0.5时，圆度C达最大值。
又因为
dH/dp1 = -log(p1)-1 +log(1-p1)+1= log((1-p1)/p1)                      (3-4-4)
所以也有
当 p1<0.5时，信息熵H单调递增，而当 p1>0.5时，信息熵H单调递减。
在p1 = 0.5时，信息熵H达最大值。 (3-4-5)

由于圆度C与信息熵有完全相同的分段单调变化趋势，所以在任何条件下最大的圆度
C都决定最大的信息熵。

因为对于矛盾体,张学文复杂度=NH ，所以在任何条件下最大的圆度C都决定最大的
张学文复杂度。

因为对于矛盾体玻尔兹曼几率 W= N！/(n1!*n2!)
这其中N为个体总数。所以根据斯特林公式，当N>>1时有
logW/N =信息熵H
这就证明了在任何条件下最大的圆度C都决定最大的玻尔兹曼几率。

当个体总数N一定时，分布函数的发生概率P完全由玻尔兹曼几率W所决定。
这就证明了在任何条件下最大的圆度C都决定最大的分布函数的发生概率。

[证毕]

下图是对信息熵H随圆度C的增加而单调增加的仿真。


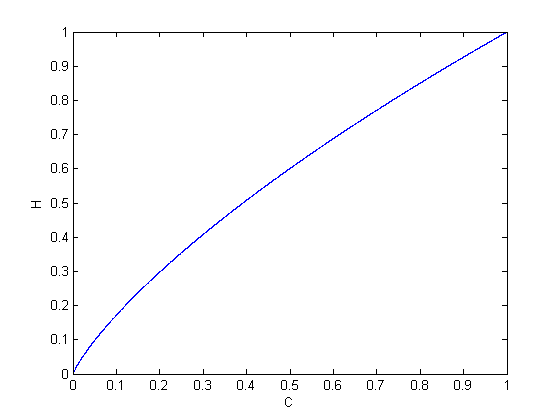
图四

3.5. 另外一种不圆度和与信息熵表达式相同的圆度H
在数学上，广义集合中各种广义方向(标志值)的存在完全由该广义方向(标志值)的
权重来体现和确定。换句话说广义方向(标志值)的权重就是广义方向(标志值)的数
学化身。从哲学高度上来看广义方向(标志值)的权重就是各种“自我”或“小我”
的数学化身。

我们用pi (i=1, 2,...,n) 来分别代表各个广义方向(标志值)的权重。
由于 对数 log(pi) 随pi的增长而单调增长，所以 对数 log(pi)也是各种“自我”
或“小我”的数学化身。

在广义集合中，所谓组成概率或成份概率就是各广义方向的权重。所以
Hn = p1log(p1) + p2log(p2) + ...+pnlog(p2)   (3-5-1)
中的Hn就是广义集合的“平均自我”或广义集合的“我执”的统计平均值。
很容易在数学上严格证明：
(a)对于矛盾体而言，矛盾双方越不平等，广义集合的“平均自我”Hn就越大；
(b)对于多维而言，最大的“平均自我”Hn对应最大的各广义方向之间的不平等，而
最小的“平均自我”Hn对应最小的各广义方向之间的不平等。
据此我们引入另一种一般性的不圆度：
既然“平均自我”最小就意味着最平等,最大就意味着最不平等,那么我们就有理由用
“平均自我”距离其最小值的距离来恒量广义集合的不圆度。
也就是说：
可以认为
不圆度 = 平均自我 - 最小平均自我 = Hn - (- log(n)) =Hn + log(n) (3-5-2)
那么圆度H = 某个常量 - 不圆度 (3-5-3)
我们就把这个常量选成 log(n)
因此有：
圆度H = log(n) -(不圆度) = -Hn =-p1log(p1)-p2log(p2)-...-pnlog(pn) (3-5-4)
显然圆度H与信息熵的表达式相同。

四、由“新皇帝”到“新皇室”
由上述论证结合泛泛系理论的本然动力学[2]，稍加论证就可以把张学文先生所谓的科学“新皇帝”修正和扩展成一个科学“新皇室”：

科学“新皇帝”的“祖父祖母”：
一切事物的本然独立而不改；
|
|
|
科学“新皇帝”的“父母”：
本来无一切指向性和由此产生的泛泛系本然动力。泛泛系本然动力迫使一切广义集
合都尽量逼近各向平等或在极坐标系上的形成给定约束条件下的极大圆性分布。
|
|
|
科学“新皇帝”：
最大圆度定律：
广义集合必须服从给定约束条件下的最大圆度H分布
|
|
|
科学“新皇帝”的“皇太子”和“公主”：
最大熵原理、最大信息量原理、最大复杂度原理、最大玻尔兹曼几率原理、最大概
率原理等等。

五、结语
本文提出了泛泛系圆度决定论和两种不同的广义集合的圆度度量：圆度C和圆度H。强调指出促成广义集合形成的根本动力是泛泛系本然动力，它迫使一切事物回归无一切指向；决定广义集合形成的根本规律是约束条件下的最大圆度定律，它派生出最大熵原理、最大信息量原理、最大复杂度原理、最大玻尔兹曼几率原理、最大概率原理等科学原理。


参考文献
[1]张学文. 组成论，合肥：中国科学技术大学出版社，2003。
[2]冯向军，泛泛系本然动力学的根本原理和应用[EB]，世界华人一般性科学论坛，第2卷，第12期，总第18期，2006年12月。http://www.aideas.com/forum18.htm
[3] http://www.qiji.cn/forum/ftopic5250.html[/b][/color][/size]