3.2 ZQB6311编码
一种非线性全息编码方法及其运算方法
张 启 斌
河北中烟工业公司 ,张家口 075000
E-mail:fu.sheng163@tom.com
摘要:现代数学和计算机所涉及的数制系统,即记数方法,均是“线性结构”的位值制,如:十进位值制、二进位值制。本文阐述了一种“累值制+位值制”混编技术的数制系统,即非线性全信息编码方法,简称全息编码,或ZQB编码,其优点是:涵盖和超越了传统线性数制,能够较好地承载“数”的原始信息;编码灵活多样,且不会产生“禁用码”。其中的ZQB5211编码,优于目前计算机使用的BCD十进制编码(不含禁用码),本文对其运算方法亦进行了实例讲解。
关键词:累值制;全息编码;公式;ZQB5211;
A kind of not the line whole information codes method and its calculation methods
Zhang Qi-bin
The " Chinese tobacco industry company" of Hebei, ZHANGJIAKOU City,075000
E-mail :fu.sheng163@tom.com
Summary:The traditional arithmetic figure all is the record method of the " line", for example:Binary system.What this text expatiate is a kind of" addend system+ digit place the system" of the admixture codes of record the few method:A kind of not the line whole information codes method, the simple name is called the coding of ZQB, advantage is:Can express" number" of primitive information;Code the diversification, and do not imply" forbid to use the code".Among them of the ZQB5211 codes, ising a very nice ten enter the system codes, this text carries to calculate the method to also proceed the elucidation to it.
Key words:addend system;The coding of all informations;Formula;ZQB5211;
1.引言
“系统科学是关于整体涌现性的科学,系统学是在基础科学层次上刻画整体涌现性的概念体系。所谓整体涌现性,意指各个组成部分不具有,但把它们整合在一起形成系统时,其整体具有的那些特性。最通俗的表述就是1+1≠2。……只要系统包含相异的成分,就会产生整体大于部分之和的涌现特性。(苗东升《凡中国人提出的新东西一律不予理睬的做法是一种殖民地心态》)
现代数学和计算机所涉及的数制系统,即记数方法,均是“线性结构”的位值制,如:十进位值制、二进位值制。从自然科学由简到繁发展规律看,人类最先学会和使用的记数方式,当是数手指、刻痕、结绳等最为简单的累值记数方式,也即累加“个”的方式。笔者把这种近乎自然的、可直观表示物质“个”信息的“数手指”、“结绳”、“刻痕”等累值记数方式,命名为“累值制”。
本文从累值制数理逻辑出发,阐述了一种“累值制+位值制”混编技术的数制系统,即非线性全信息编码方法,简称全息编码,或ZQB编码,其优点是:涵盖和超越了传统线性数制,能够较好地承载“数”的原始信息;编码灵活多样,且不会产生“禁用码”。其中的ZQB5211编码,优于目前计算机使用的BCD十进制编码(不含禁用码),本文对其运算方法亦进行了实例讲解。
2.“非线性”数制
数制即记数体制,它是按照一定规律表示数值大小的记数方法。传统线性数制,即位值制的表现形式是:An…A2A1A0 ——其累值信息,均被人们简略和跨越了。例如:甲乙班共有78名学生(其中甲班42名学生,乙班36名学生)。我们单从“78”数字中,是看不到“42”和“36”两个原始数态信息的。
下面,我们分析一下42和36两个原始数态信息,如何使用“等权”数符进行累值,即衍变到数字78的过程:
4120+3160=(4+3)1(2+6)0=7180
上述使用“等权”数符进行累值的过程(5+2)1(2+6)0 ,其去掉括号和加号后为4326,无疑,4326也是一种记数法:4与3、2与6之间为累值制关系,43与26之间为位值制关系。
笔者把上述这种“累值制+位值制”混编技术的数字系统,称为非线性全信息编码方法,简称全息编码,或ZQB编码。其“位”与“位”之间的关系,亦突破了传统“线性”数制的限制,可为不同的进制关系。
3. 全息编码
全息编码的编码方法,我们概括为如下公式:其“累值结构”和“位值结构”,我们根据“需要”可以任意锁定,即最终形成一种不规则的、非线性的全信息编码方案。
ZQB=(A n+B n+C n+…)n…(A2+B2+C2+…)2(A1+B1+C1+…)1(A0+B0+C0+…)0
注:加号与加号之间为累值制结构关系;括号与括号之间为位值制结构关系。
由于篇幅所限,以下我们仅对二元全息编码进行讨论;多元全息编码,我们以此类推。
3.1 ZQB51111编码
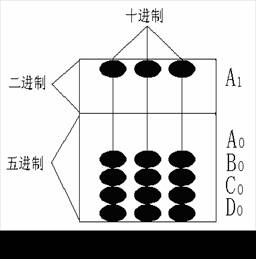
这是一组二元十进制的全息编码方案,即中国算盘的实用编码(算珠的一上一下为“0”“1”)。其编码套装和锁定了如下公式中的系统结构(黑体字母):
ZQB=(A+B+C+…)n…(A+B+C+…)2(A1+B1+C1+…)1(A0+B0+C0+D0…)0
也即:ZQB51111 =A1(A0+B0+C0+D0)0 = A1A0B0C0D0
|
十进制数 X |
ZQB51111编码 A1 A0 B0 C0 D0 |
|
0 |
0 0 0 0 0 |
|
1 |
0 0 0 0 1 |
|
2 |
0 0 0 1 1 |
|
3 |
0 0 1 1 1 |
|
4 |
0 1 1 1 1 |
|
5 |
1 0 0 0 0 |
|
6 |
1 0 0 0 1 |
|
7 |
1 0 0 1 1 |
|
8 |
1 0 1 1 1 |
|
9 |
1 1 1 1 1 |
|
10 |
0 0 0 0 0 |

3.2 ZQB6311编码
这是一组二元十二进制的全息编码方案,其编码套装和锁定了如下公式中的系统结构(黑体字母):
ZQB=(A n +B n +C n +…)n…(A2+B2+C2+…)2(A1+B1+C1+…)1(A0+B0+C0+…)0
也即:ZQB6311 = A2A1(A 0+B0)0= A2A1A0B0
|
十进制数 X |
ZQB63111编码 A2 A1 A0 B0 |
|
0 |
0 0 0 0 |
|
1 |
0 0 0 1 |
|
2 |
0 0 1 1 |
|
3 |
0 1 0 0 |
|
4 |
0 1 0 1 |
|
5 |
0 1 1 1 |
|
6 |
1 0 0 0 |
|
7 |
1 0 0 1 |
|
8 |
1 0 1 1 |
|
9 |
1 1 0 0 |
|
10 |
1 1 0 1 |
|
11 |
1 1 1 1 |
|
12 |
0 0 0 0 |
3.3 ZQB5211编码
这是一组较为复杂的二元十进制的全息编码方案,其编码套装了两次“公式”:
第一步,首先制定一组ZQB311全息编码方案(六进制),其编码套装和锁定了如下公式中的系统结构(黑体字母):
ZQB=(An+Bn+Cn+…)n…(A2+B2+C2+…)2(A1+B1+C1+…)1(A0+B0+C0+…)0
也即:ZQB311=A2(A1+B1)1 =A2A1B1
第二步,把上述ZQB311编码的A1 部分,二次套装如下公式中的系统结构(黑体字母):
ZQB=(A+B+C+…)n…(A2+B2+C2+…)2 (A1+B1+C1+…)1(A0+B0+C0+…)0
也即:ZQB5211=A2(A’1A’0+B1)1=A2A’1A’0B1
|
十进制数 X |
ZQB5211编码 A2 A1 A0 B1 |
|
0 |
0 0 0 0 |
|
1 |
0 0 0 1 |
|
2 |
0 0 1 1 |
|
3 |
0 1 0 1 |
|
4 |
0 1 1 1 |
|
5 |
1 0 0 0 |
|
6 |
1 0 0 1 |
|
7 |
1 0 1 1 |
|
8 |
1 1 0 1 |
|
9 |
1 1 1 1 |
|
10 |
0 0 0 0 |
3.4 ZQB8421编码
这是一组特殊的全息编码方案,也即传统的二元十六进制编码方案。我们在此赘述,是为了说明:现代数学和计算机所涉及的线性数制系统,仅仅是全息编码的一种特例;换句话说,全息编码涵盖和超越了传统线性数制系统。如下,其编码锁定了公式中如下的系统结构(黑体字母):
ZQB=(An+B n+C n+…)n…(A2+B2+C2+…)2(A1+B1+C1+…)1(A0+B0+C0+…)0
也即:ZQB8421=A3A2A1 A0
|
十进制数 X |
ZQB8421编码 A3 A2A1 A0 |
|
0 |
0 0 0 0 |
|
1 |
0 0 0 1 |
|
2 |
0 0 1 0 |
|
3 |
0 0 1 1 |
|
4 |
0 1 0 0 |
|
5 |
0 1 0 1 |
|
6 |
0 1 1 0 |
|
7 |
0 1 1 1 |
|
8 |
1 0 0 0 |
|
9 |
1 0 0 1 |
|
10 |
1 0 1 0 |
|
11 |
1 0 1 1 |
|
12 |
1 1 0 0 |
|
13 |
1 1 0 1 |
|
14 |
1 1 1 0 |
|
15 |
1 1 1 1 |
|
16 |
0 0 0 0 |
4.全息编码之运算
4.1运算规则
首先,我们讨论一下二元全息编码的加法规则:
(1) 0+0=0
(2) 0+1=1
(3) 1+0=1
(4) 1+1=10 (Cn=1)
(5) 1+1=11 (Cn=0)
上述1~4条规则,为传统二进制加法规则。
我们把上述第4条规则,又细分为两种情况,即增加了第5条规则:Cn为某数位的“进位”,在累值过程中,当某数位发生进位,即Cn=1时,该数位归“0”;相反,在累值过程中,某数位没有发生进位,即Cn=0,那么该数位不归“0”。
口诀:见一进一,溢位归零(不溢位不归零)。
下面,我们再讨论一下二元全息编码的减法规则:
(1) 0-0=0
(2) 0-1=11(有借位)
(3) 1-0=1
(4) 1-1=0 (Bn=0)
(5) 1-1=11 (Bn=1)
上述1~4条规则,为传统二进制减法规则。
我们把第4条规则,又细分为两种情况,即增加了第5条规则:Bn为某数位的“借位”,在减值过程中,当某数位发生借位,即Bn=1时,该数位置“1”;相反,在减值过程中,某数位不发生借位,即Bn=0时,该数位不置“1”。
口诀:见一退一,借位置一(不借位不置一)。
4.2正码、副码(以及原码、反码、补码)
ZQB5211编码,为二元十进制编码,其系统结构为“四”,最大编码容量为十六。传统计算机BCD十进制编码,采用其中的十个编码,把剩余的六个编码设为了“禁用码”,并严加禁用;ZQB5211全息编码与之不同,它把十六个编码分为了十组编码,因此把传统概念的“禁用码”,转化为了一种能够参予运算的“副码”。如下为ZQB5211全码表(含副码):
|
十进制数 |
原码 |
反码 |
补码 |
|
0 |
0000 |
1111 |
0000 |
|
1 |
0001 0010* |
1110* 1101 |
1111 |
|
2 |
0011 0100* |
1100* 1011 |
1101 |
|
3 |
0101 0110* |
1010* 1001 |
1011 |
|
4 |
0111 |
1000 |
1001 |
|
5 |
1000 |
0111 |
1000 |
|
6 |
1001 1010* |
0110* 0101 |
0111 |
|
7 |
1011 1100* |
0100* 0011 |
0101 |
|
8 |
1101 1110* |
0010* 0001 |
0011 |
|
9 |
1111 |
0000 |
0001 |
ZQB5211全码表,囊括了系统全部的十六个编码:带*号的0010*、0100*、0110*、1010*、1100*、1110*为副码,分别为0001、0011、0101、1001、1011、1101六个主码的副码。主码共计十个,副码六个。
全息编码为有权编码,ZQB5211编码之数权为5211。例如:1011编码(主码)的数值为:5×1+2×0+1×1+1×1=7;1100编码(副码)的数值为:5×1+2×1+1×0+1×0=7 。主码与副码统称原码;原码如果“按位求反”,我们可以得到反码(与传统二进制编码求反码方法完全一样);反码加1,我们可得到补码(与传统二进制编码求补码方法亦完全一样)。
4.3 全息编码之运算
4.3.1加法运算
例1:有两个十进制数,A=37,B=82。
我们把A、B两数翻译为ZQB5211编码:A=0101 1011;B=1101 0011 。
把A、B两数列竖式,并按上述加法运算规则相加:

结果为:1,0010 1111(含副码),即119,运算正确。
4.3.2减法运算
例2:有两个十进制数,A=86,B=73。
我们把A、B两数翻译为ZQB5211编码:A= 1101 1001;B=1011 0101 。
把A、B两数列竖式,并按上述减法运算规则相减:
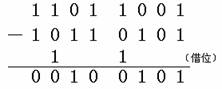
结果为:0010 0101(含副码),即13,运算正确。
4.3.加补码方法(减法)之运算
全息编码同传统方法一样,也可以利用加补码方法来化简减法计算。首先我们把ZQB5211编码格式化,如下:
|
十进制数 |
ZQB5211格式化 |
||
|
原码 |
反码 |
补码 |
|
|
+9 |
01111 |
01111 |
01111 |
|
+8 |
01110* 01101 |
01110* 01101 |
01110* 01101 |
|
+7 |
01100* 01011 |
01100* 01011 |
01100* 01011 |
|
+6 |
01010* 01001 |
01010* 01001 |
01010* 01001 |
|
+5 |
01000 |
01000 |
01000 |
|
+4 |
00111 |
00111 |
00111 |
|
+3 |
00110* 00101 |
00110* 00101 |
00110* 00101 |
|
+2 |
00100* 00011 |
00100* 00011 |
00100* 00011 |
|
+1 |
00010* 00001 |
00010* 00001 |
00010* 00001 |
|
+0 |
00000 |
00000 |
00000 |
|
-0 |
10000 |
11111 |
00000 |
|
-1 |
10001 10010* |
11110* 11101 |
11111 |
|
-2 |
10011 10100* |
11100* 11011 |
11101 |
|
-3 |
10101 10110* |
11010* 11001 |
11011 |
|
-4 |
10111 |
11000 |
11001 |
|
-5 |
11000 |
10111 |
11000 |
|
-6 |
11001 11010* |
10110* 10101 |
10111 |
|
-7 |
11011 11100* |
10100* 10011 |
10101 |
|
-8 |
11101 11110* |
10010* 10001 |
10011 |
|
-9 |
11111 |
10000 |
10001 |
例3:有两个十进制数,A=46,B=78 。
我们参照上述表格,把A、B两数翻译为ZQB5211格式化编码:A= 0,0111 1001;B=1,1011 1101 。
把A码、B码各求补码:A= 0,0111 1001;B=1,0100 0011(含补码) 。
把A补码与B补码列竖式,并按上述加法运算规则相加::

与传统加补运算一样,得数需再求补一次,即结果为1,0101 0011,也即-32,运算正确。
4.4正副码之转换
正码副码之转换,非常简单。方法如下:

5.结束语
苗东升教授说:“建立系统学,发展系统论,就得给出整体涌现的科学论证”。累值制是人类古老的、近乎自然的一种记数体制,它较大程度的反映了自然界原发态的数学本质。本文从累值制数理逻辑出发,阐述的“累值制+位值制”混编技术的数制系统,即非线性全信息编码方法,及其利用余码(副码)参予运算,从而使得运算较少发生进位,最终提高了运算效率。这种“累值制+位值制”混编技术的数制系统,即1+1≠2的“整体涌现”,充分说明了系统科学的整体涌现原理是正确无疑的。
灵活多样的非线性全息编码,为当代信息科学、特别是计算机语言科学的研究和发展,提供了一种的新方法、新思路。
参 考 文 献
1. 苗东升,凡中国人提出的新东西一律不予理睬的做法是一种殖民地心态.组成论(序言3)[M].安徽科学技术大学出版社,2003.12.
2. 武庆生、邓建.数字逻辑[M].北京:机械工业出版社.2004.4.
3. 王明臣,微型电子计算机数字电路基础[M].北京:中国电子学会普及工作部.1985.
4. 张启斌.中国珠算“累值制”数理逻辑——兼论莱布尼茨所谓“二进制”发明[EB]. 世界华人一般性科学论坛(期刊)第1卷第3期(.http://www.aideas.com/forum.htm), 2005,9.
5. 张启斌.累值制数理逻辑及其编码、组合编码之研究[C].全国信息科学交叉学术研讨会.北京师范大学,2005.11.5~7.
6. 张启斌. 累值制数理逻辑与物源数态信息之分析[EB]. 中国科技论文在线(http://www.paper.edu.cn),200602-340.
7. 张启斌.信息是一个以“个”为基本量化单位的物理名称[EB].中国潜科学论坛(http://potentialscience.org/),2005.12-28.