译码模型:一个对称的色觉机制模型
提要 一个对称的色觉模型译码模型被建立,它可以 使 我们更好地理解颜色视觉。其中采了一种新的连续值逻辑或模糊逻 辑, 其工作方式和数字电路中常用的3-8译码器相似。 和流行的阶 段模型不同, 译码模型中有四对互补色:兰黄、绿绛、红青和白黑。 通过译码模型, 色觉进化,颜色色盲和人对颜色的知觉能被更简 洁地说明; Young和Helmholtz的三色素说和Hering的互补色说 可以得到更自然的统一。
1 引言
Young和Helmholtz的三色素理论同Hering的互补色理论一 直竞争了很长时间。 一个被广泛接受的折中观点是:颜色信号在 视细胞阶段以三色素形式存在,而在视神经阶段以互补色形式存 在。 带有这一观点的数学模型是阶段模型(Judd,1949)。 现在有 许多改进的版本((Hurvich et al.,1957; Walraven,1961; Hunt, 1 982 and 1987; Nayatani at el.,1986; Seim at el., 1986)。 然而,为什么颜色信号以这种方式被处理,并且颜色视觉是怎 样进化的? 回答仍然不清楚。 为了更好回答这些问题, 作者建 造了一个颜色视觉模型, 名叫译码模型(鲁晨光,1986 ,1989) 。
我们也可以说译码模型是阶段模型的一个新版本, 但是和 流行的阶段模型相比较,译码模型采用了逻辑运算而不是算术 运算;它严格对称并产生三对彩色信号--兰黄、绿绛和红青, 而不是象流行的阶段模型中那样是两对:兰黄和红绿。
注意, Hering理论中的“红”和“ 绿” 象流行的阶段模型 中的一样而和Young-Helmohoitz理论中的“红”“绿” 不同。 用Young-Helmholtz理论或彩色电视工业的术语来说, “红” 在红-绿 一词中意指一种介于红和绛之间的颜色;“ 绿”在 “红-绿”一词中意指一种介于绿和青之间的颜色。颜色名称的 差别并不重要,重要的是:是否三对单纯彩色或原色(unique colours) 可能存在。
有人或许认为心理学实验已经证明四种单纯彩色存在, 因 而产生六种纯彩色的模型是不合理的。 然而,我们坚持自己的观点 有不少理由:
1) 只有四种单纯彩色存在并不是最终结论, 有些人仍然坚持说有多于四种单纯彩色存在(Hardin,1985)。
2) 生理学实验表明有多于两种彩色互补信号存在于猴类视网 膜中(de Monasterio, at el., 1975)。
3) 具有对称性的模型似乎更好,而对称的色觉模型要求有六种单纯彩色存在。
4) 颜色视觉正在进化,我们能想象单纯彩色的数目正在由四种变 为六种, 如果说在红色和绛色,绿色和青色之间存在类似性, 这只是由于视网膜中有些构造正处于较低的水平上。
第五个理由将在后面谈及。
译码模型已经通过预测颜色知觉(colour appearance)的θ-rc-z颜色 系统得到验证(鲁晨光,1989), 该系统的匀色性和CIE(国际照明协会)LAB颜色 系统的匀色性相当。 本文主要讨论模型的数学方面并解释各 种颜色现象。
2 颜色视觉的译码模型
现在我们讨论模型的数学方面而不考虑颜色三接收器输出信号 B,G,R是怎样从颜色光学数据转换来的。
2.1 模糊3-8译码器
二进制3-8译码器频繁地使用于计算机和数字电路中,用作 八中选一工作。 如果B,G,R是二进制开关变量, 即B,G,R取值于 集合{0,1}中, 并作为3-8译码器的三个输入, 那么八个输出将 是[B G R], ], [B G R], [B G R], [B G R], [B G R], [B G R]and [B G R] ( [...]表示逻辑表达式, B 表示逻辑非--下划线是由于排版原因,本该是上划线)。比如, 当B=G=0、 R=1时, [B G R]=1, 其他等于0。
设B,G,R代表三种视锥细胞的输出, 一种颜色用矢量(B,G,R)表示。 于是[B G R], [B G R ],…, [B G R ]分别表示红、黄 、...、白八种颜色信号的大小(见表1)。
表1 B,G,R和八个输出码或颜色信号的关系
| B G R | Black ness [B G R] |
Red- ness [B G R] |
Yellow- ness [B G R] |
Green- ness [B G R] |
Cyan- ness [B G R] |
Blue- ness [B G R] |
Mage- ntaness [B G R] |
White- ness [B G R] |
0 0 0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 0 1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 1 1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 1 0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 1 0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 0 0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 0 1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 1 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
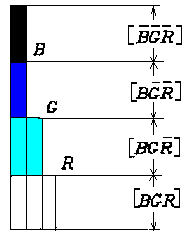
现在我们假设B、G、R由二进制开关变量变为模糊开关变量, 即B、G、R取值于连续值集合[0,1]。 使用特殊的专为模型而创建 的模糊逻辑,我们能推广二进制3-8译码到模糊3-8译 码(鲁晨光,1991)。 输出码的值图示如图1。

图1 输入码R、G、B和八个输出码之间的关系(B>G>R时,四个输出码的值如图所示,其他的等于0)
我们用max(a,b)表示a和b中较大者, mim(a,b)表示a和b中较小者,其他类推。于是
[B G R ]= 1-max(B, G, R)
[B G R ]= max(0, R-max(B, G))
[B G R ]= max(0, min(G, R)-B)
[B G R ]= min(B, G, R)
(1 )
其他输出码计算类似。
2.2 θ-rc-z系统
现在的问题是怎样由B、G、R得到分别表示色调,彩度和明度的θ、rc、z。对于任一颜色(B,G,R), 存在等式
(B,G,R) = [B G R ](0,0,1)+[B G R ](0,1,1)+ [B G R ](0,1,0)
+[B G R ](1,1,0) + [B G R ](1,0,0)+ [B G R ](1,0,1)+ [B G R](1,1,1)
(2)
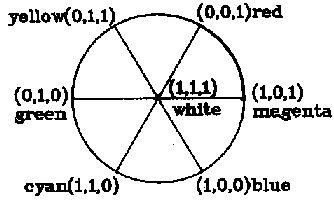
图2 颜色(B,G,R)的分解
这意味着任何颜色能被分解成白色和六种单纯彩色不同比率相加。等式中,(0,0,1)表示最饱和红色, 即单纯红色; 系数颜色(B,G,R)红的程度。 其他类推。
巧妙的是, 对于给定的任一颜色, 等式(2)中右边只有三项可能同时不为0, 而且这三项必然位于 图2中六个扇区之一的三个顶点上。 所以等式(2)可以变为
(B,G,R)= m1 e1 + m2 e2 + m3 e3
(3)
这里, e1、 e2、 e3是三个非0项中的三个基矢, 且e3=(1,1,1); m1、 m2分别是相应e1、 e2的输出码的系数或其大小。 m3=[BGR] 是白度(白的程度)。
假设e1和e2所在的角度分别为θ1和θ2, 令
θ=(m1θ1+m2θ2)/ m1+m2+m3
rc = m1 + m2
z = m1 + m2 + m3 ( or z = max(B,G,R))
rs = rc / z
(4)
θ、 rc、 z、 rs便分别代表(B,G,R)的色调 θ(hue)、 彩度(colourfulnes s)、明度 (brightness和饱和度(saturation)(如果B、G、R是光谱三刺激值X、Y、Z通过 适当的线 性和非线性变换得到的(鲁晨光,1989))。 根据译码模型, 明度、彩度、白度 ( whiteness)、 黑度(blackness)和B、G、R之间的关系如图三所示, 图中 med(B,G,R)是B、G、R 中中间的一个或第二大者。
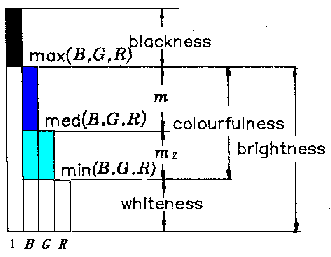
图3 B,G,R和明 度、彩度、白度及黑度之间的关系
比如, med(1,3,5)=3; med(1,2,5)=2; med(1,5,5)=5; med (1,1,5)=1。
2.3 互补处理
我们用文氏图说明互补处理的本质。 令∪、 ∩、'代表并、 交、补三种集合运算,B、G、R分别代表三个圆形区域(见图4)。为 了方便, 我们也用 - 作为补运算, 并且有时省去∩。
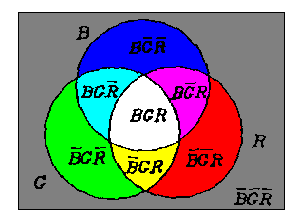
图4 显示互补处理本质的文氏图
于是R、 ...、BGR可分别表示三个圆圈划分出的8个 区域。
从B、G、R, 我们首先得到
M = BG∪BR∪GR
(5)
它代表B、G、R中两个或三个相交的区域。 然后我们得到
B M = B G R , B M = B G R ;
G M = B G R , G M = B G R ;
R M = B G R , R M = B G R ;
(6)
如果圆形区域B、G、R分别被蓝、绿、红色光照明, 三对互补色将显 示在六个区域上。 比如, 蓝色和黄色将分别显示在区域B M = B G R 和 B M = B G R 上.
现在我们用B、G、R表示三接收器输出, 它们取值于集合[0, 1]。 集合运算被模糊逻辑运算∨、∧、-代替(∨表示取大,∧ 表示 取小且可省略)。 首先我们获得med(B, G, R):
M =med(B, G, R) =[BG∨ BR∨ GR]
or M =max(min(B, G), min(B, R), min(G, R))
( 7)
然后得到互补信号:蓝-黄(MBY)、绿-绛(MGM)和红-青(MRC)。 下 面计算惊人地简单。
![]()
![]()
![]()
(8)
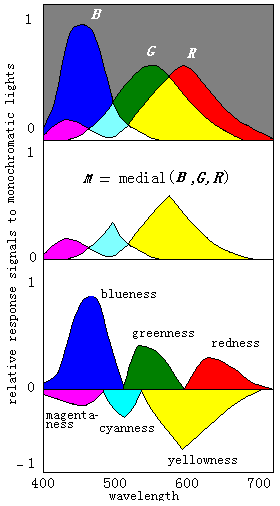
图5 相应不同单色光的互补处理首先计算出B、G、R中间的一个, 然后分别从M中减去B,G,R得到三对彩色互补信号
相应不同单色光的互补处理如图5所示。 为了方便,其中三响应 曲线是假设的。 我们也可以把图5上面的部分当做文氏图。 其中 有8个划分的区域, 一垂直线在某一区域上的长度就是相应的单 纯色信号的大小。 不同单色光引起的颜色视觉变化可由这些区 域得到很好说明。
2.4 物理模型
译码模型中互补处理的原理框图如图六所示。 为了演示颜 色信号在视网膜和大脑皮层的处理, 笔者已经做出了一个完整 的颜色视觉物理模型(参见图6和图7), 它的运行正象期望的那样。
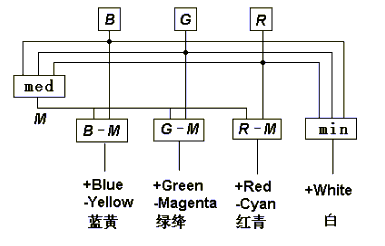
图6 译码模型中的对称互补处理
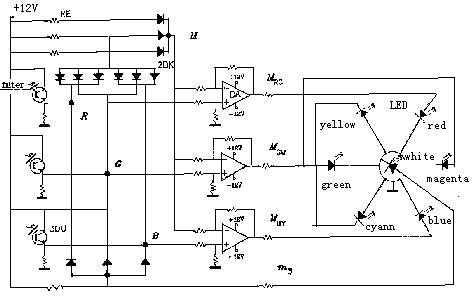
图7 颜色视觉物理模型原理图
其中3DU是光电三级管, 它模拟视锥细胞; DA是差动放大器,它模拟双极细胞; LED是发光二极管, 它被假设为脑皮层上的色觉细胞; RE是电阻, 2DK是二极管。 左上角的二极管和电阻 阵列被假设为水平细胞, 它产生输出med(B,G,R).
该物理模型认为: 在脑视皮层应有7种色觉细胞, 它们接收 白色和六个单纯彩色信号; 大脑通过简单的加法运算得到明度 和彩度, 通过求重心的方法产生色调。 或许也有一些颜色信号 的处理处于较低的水平, 比如, 某些白色感觉细胞可能直接接收从视锥 细胞或视杆细胞来的快速传递的信号 (Kaplan, 1982)。 译码模 型并不包含这些内容,因此它不提供象CIE XYZ系统中的光度或 象Munsell系统中的光值V那样的测度, 它提供的只是明度测度z 。
3 色觉进化和色盲
3.1 色觉进化
根据译码模型, 我们能通过三敏感曲线的变化简单地说明 色觉进化(见图8)。
请想象曲线R(λ)和G(λ)逐渐相互靠近以至合 二为一, 取名为Y(λ), 我们将看到代表红、绿、青、绛的区域逐渐 消失。 进一步, 让B(λ)和Y(λ)逐渐相互靠拢以至合二为一, 取 名为W(λ), 我们将看到表示蓝和黄的区域也逐渐消失, 最终只 有白色和黑色区域存在。 因此, 我们可以想象颜色视觉是以相 反的方式进化的。
我们得到结论: n种色敏感细胞可以引起2n种完全不同 色觉(对于n=1,2,3)。 当n=4时, 结论看来也是正确的。我们建 立了一个对称的可用于机器人的四原色色觉机制数学模型,其 中除了 白色” (1,1,1,1)和黑色(0,0,0,0),有14种单 纯彩色”, 它们可以对称地放在一个球面上(鲁晨光,1987)。 由此我们可以得到一个颜色球它有许多牛顿色盘所具有的 性质。
3.2 色盲
色盲已被许多研究者所讨论(Hsia at el。, 1965)。 现在 〖WTBX〗我们可以通过视细胞敏感曲线的相互靠近从而更方便地解释色盲。 比如, 全色盲可以说是因为色敏感曲线B(λ)、G(λ)、R(λ)还没有 从一种分裂出来; 红绿色盲可以说是因为曲线G(λ)和R(λ)还没 有从Y(λ)分裂出来。 从这一观点看, 有些色盲被称之为“红色 盲”或“绿色盲”只是由于Y(λ)波峰的波长或长或短。对蓝绿色 盲也可作类似解释。 各种色盲也可以通过让两个或三个3DU接收 相同的输入信号来模拟。
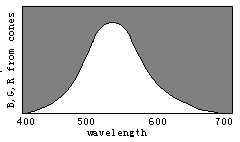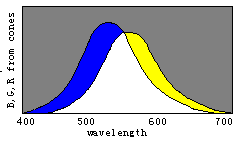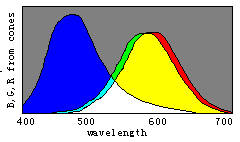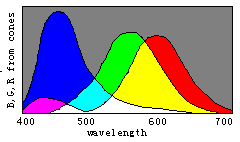
图8 通过敏感曲线的分裂图解色觉进化
具有一种锥细胞的人只能察觉两种完全不同颜色:黑和白; 随着W(λ)分裂成B(λ)和Y(λ), 人能渐渐能分辨出四种完全不同 颜色: 蓝、黄、白、黑。 随着Y(λ)分裂成G(λ)和R(λ), 人能渐渐地 能见到更多完全不同颜色
4 讨论
为了更好理解颜色视觉, 我们讨论如下问题。 我们可以假设脑视皮层只有三种色觉细胞, 每一种以最简 单的方式接收一种直接来自色敏感细胞的信号。 但是, 为什么 色觉机制给我们多于三种完全不同色觉呢? 我们的回答是: 为 了使人脑更容易区分不同物体, 色觉机制预先处理了颜色信号, 以至物体的光谱特殊性能得到更好反映。 不难理解, 可见的单 纯色越多, 颜色视觉能提供的信息就越多。 信息的解释是我们 坚持自己关于单纯色数目的见解的第5个理由。
可幸的是, 我们关于颜色信息的考虑导致了一个改进的信息理论(鲁晨光,1990), 这一理论可以提供颜色信息和主观的颜色分辨 率之间的关系。
另一个问题是:为什么颜色信号在视细胞阶段以三基色形 式存在而在视神经阶段以互补色形式存在? 我们的回答是:这是由 于经济的缘故。 从物理模型我们能发现, 以这种方式,六种 单纯彩色信号能被最为经济地产生和传递。
和流行的其中只有两对彩色互补信号的阶段模型相比较, 除了在回答上面两个问题时显示的优点外,译码模型还具有下 面优点:
1) 译码模型更加简洁, 对称且不带修正参数。
2) 用它可以更加方便解释色盲和色觉机制进化。
3) 译码模型中, 从理论上讲, 一个单纯彩色(unique color)可以唯一地(uniquely)产生。 比如, 当(B,G,R)=(0,0,1)时, 只有红度不是0, 白度和其他六个量皆是0。 而在流行的阶段模 型中, 除了(B,G,R)=(0,0,0), 白度在任何时侯都不为0。 这就 缩小了可能的色觉空间, 从信息的观点看, 这是不好的。
4) 译码模型更和显示在电视屏幕上的颜色混合规律相容。
5) 通过译码模型可以更方便地解释颜色负后象现象。 比 如, 当R色敏感细胞因光照而敏感特性下降时, 对于白色, 代表 青色信号大小的[BG***]将由0增加到大于0, 以至白色看起来发青。
比较某些阶段模型, 比如Hunt模型(Hunt,1987), 译码模 型也有一些缺点。 例如, 它只考虑颜色信号的主要处理方式, 而不考虑视杆细胞、适应和光度Y之类测度。 这和建立模型的目 的有关。
译码模型也能被神经生理学检验。 根据译码模型可以做两 个预言, 一是视网膜中应该存在执行取大、取小、甚至取中间运 算的逻辑门; 二是在视神经上应该存在彩色互补处理机制,它 们的响应曲线在正的和负的之间有一水平线而不是一个中性点( 见图5)。 这些逻辑门还没有被人们谈及, 要么是因为大多数实验是 用动物做的, 而它们的色觉机制不那么发达;要么是因为实验 缺少适当的理论指导。 比如, 一个广泛使用的确定互补机制的 方法是发现它的中性点(Volois,1966); 然而这种方法不适合 确定我们上面建议的互补机制。 我们相信, 前面所预言的逻辑 门和互补机制能很快被注意它们的人发现。
参考文献
[1]De Monasterio F M, Gouras P and Tollhurst D J., Trichromatic colour opponency in ganglion cells of therhesus monkey retina, J. Physiol. 25 2(1975), 197-216
[2]De Volois R L, Abramov I and Jacobs G H. Analysis of response properties of LGN cells, J. Opt. Soc. Am.56(1966),966-977
[3]Hardin C L. The resemblances of colours,Philosophical Studies 48(1985), 35-47
[4]Hsia Y and Grapham C H. Colour blindness, in Visual Perception, C. H. Grapham ed., Wiley, New York, 1965, Chap. 14, Tab.14.2
[5]Hunt R W G. A model of colour vision for predicting colour appearance, Colour Res. Appl. (1982), 95-112
[6]Hunt R W G. A model of colour vision for predicting colour appearance in various viewing conditions, Colour Res.Appl.2(1987), 293-314
[7]Hurvich L M and Jameson D. An opponent-process theory of colour vision, Psychological Review 64(1957), 384-404
[8]Judd D B. Response functions for types of vision according to the Muller theory, J. Res. Natl. Bur. Std. ,1(1949)
[9]Kaplan E and Shapley R M. X and Y cells in the lateral geniculale nucleus of Macaque monkeys, J. Physiol. 330(1982),125-143
[10]鲁晨光. 色觉新说及机制模拟, 心理学动态, (1986), 36-45
[11]鲁晨光. 机器人色觉机制模型, 机器人,1,6(19 87),39-46
[12]鲁晨光. 译码模型机器验证, 光学学报,9(1989), 158-163
[13]Lu C -G. Shannon equations reform and applications,BUSEFAL 44(1990), 45-52
[14]Nayatani Y. & Takahama K and Sobagaki H. Prediction of colour appearance under various adapting conditions, Colour Res. Appl.11(1986), 62-71
[15]Seim T and Valberg A. Towards an uniform colour space: A better formula to describe the Munsell and OSA colour scales,Colour Res. Appl. 11(198 6), 11-24
[16]Sperling H G and Harwerth R S. Red-green cone interactions in the increment-threshold spectral sensitivity of primates, Science 172(1987), 180 -184
[17]Walraven P L. On the Bezold-Brucke phenomenon, J. Opt. Soc. Am. 51(1961), 1113-1116