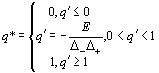投资渠道和投资容量
——Shannon信道容量理论推广

我们先看经典信息论中的信道容量定义^[27]。

给定信道P(Y|X)，信源H(X)不同，互信息I(X；Y)也不同。信道容量被定义为：给定信道P(Y|X)时，改变信源P(X)，使得当P(X)=P*(X)时，互信息I(X；Y)达最大，这个最大值就是信道容量。设P_C 是所有可能的信源构成的集合，则信道容量C的数学定义是

(9.4.1)

设X∈A＝B＝(- ∞，+∞)，叠加性噪声Z是均值为0，方差(或功率)为s ²的高斯变量; 输入为X输出为Y＝X+Z，则可以推导出信道容量为

(9.4.2)

其中P_wo和P_wi 分别是信号输出和输入功率。上式表示，和输入功率相比，噪声功率s ²越小，信道容量越大。

现在考虑投资问题。我们把未来价格矢量发生的概率分布P=(P_1，P₂，... P_M)和增值矩阵R=(R_ik)组成的对(P，R)叫做投资渠道，所有可能的投资比例矢量q=(q₀，q_1，q_2，...q_N)构成的集合是q_C ，则投资渠道的容量(简称投资容量)被定义为

(9.4.3)

其中q*是最优投资比例，它是P和R的函数，即q*=q*（R，P）。

F_r ={0.5|r₁，0.5|r₂}={0.5|D _-，0.5| D ₊)

={0.5|E- R_r，0.5|E+R_r}

其中r₁<0<r₂，E是期望收益，R_r是增值风险。最优投资比例是(因为是一维的，矢量变成标量)：

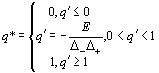(9.4.4)

当q*=q’时，投资容量为

(9.4.5)

根据泰勒级数公式，当x<1时，

(9.4.6)

因为r₁=E- d<0，所以E/d<1，因而有近似的投资容量公式

(9.4.7)

可见期望收益的平方E²很像通信系统中的信源信号功率，风险测度的平方R_r²很像是噪声功率。上式中E²/R_r²越大，投资容量越大，这和通信系统中信噪比越大，信道容量越大是一样的。

q*=0时，投资容量H*=0；当q*=1时，投资容量是

H*=0.5log[(1- D _-)(1+D ₊)]=0.5log[(1+R_r)^2- E²] (9.4.8)

假设允许透支和卖空，则q*可能大于1或小于0，H*作相应变化(不赘)。

Shannon信道编码定理告诉我们：给定信道时，只要传递的信息率小于C，我们总可以在原信源和信道之间加一个编码环节作某种编码，使得在信道输出端无失真地译出信源信号的概率无穷地接近于1；不能指望通过有限容量的信道传输过量的信息；编码的目的实际上就是使信源和信道相匹配。

在通信系统中，除了有改变信源使之匹配信道的问题，也有改变信道使之匹配信源的问题，后一问题就是保真度信息率(或信息率失真)问题。但是在投资系统中，这一问题没有实际意义，因为从数学上看，可能的投资渠道会使增值熵达无穷大。