广义信息论概要
1.研究背景
几乎每个领域都有把已有的正统理论奉为圣经,从而拒斥一切“异端邪说”的卫道士。下面我们向经典理论提几个问题,广义信息论的基本思想也由此体现出来:实际上,任何一种通信都不能完全排除信号的意义问题。经典信息理论中讨论的信息率失真问题就和信号的意义密切相关。没有意义,哪来失真?由于避免考虑意义,经典的信息率失真理论就注定了残缺不全。失真实际上就是主观信息损失,因为不考虑意义,它就只能来自人为定义,而不是由统计确定;强调统计却反而导致统计的忽视。控制系统中的预测质量本来就应该用预测提供的信息作为评价标准,因为排除意义,预测信息就无法度量。
其实,曾和Shannon合著《通信的数学理论》[28]一书的W. Weaver在该书中的一篇论文中就提出通信的三个水平:水平A——通信的技术问题,如Shannon理论研究的;水平B——考虑到语义问题;水平C——考虑到效用或价值问题。 继Weaver之后,许多学者对广义信息作了不懈的努力,建立了各种各样的广义信息测度公式[4],但是那些公式皆很难被理解和应用——如用于天气预报或股市预测。 笔者为了解释自己建立的色觉机制数学模型——色觉的译码模型——的合理性,从1988年开始研究感觉信息,后来又研究语义信息,继而建立了自己的广义信息理论。新的广义信息测度既和常识吻合,也是Shannon信息测度的自然推广。笔者以为自己找到了人们要找的东西。鲁氏广义信息论概要
1.集合Bayes公式和三种概率的区别和联系 设信源信号集合(或字母表)A={x1,x2,...,xm},信宿信号集合B={y1,y2,...,yn},X和Y分别是取值于A和B中元素的随机变量。已知P(xi)和P(yj|xi)可以求出反条件概率P(xi| yj)=P(xi)P( yj|xi)/P( yj) (9.6.1)
这就是Bayes公式,其中![]() (9.6.3)
(9.6.3)
Q(Aj)=Q(yj为真)
Q(Aj|xi)=Q(yj为真|xi)= Q(yj(xi)为真)
Q(xi|Aj)=Q(xi|yj为真)
鲁氏广义信息论中用到三种概率:
我们以下雨为例说明三种概率的区别。
1) 由历年气象数据统计得到的某地某月某日无雨的概率为客观概率——即数理统计所使用的概率,后面有时也简称为概率,如P(xi),P(yj|xi)等即是;
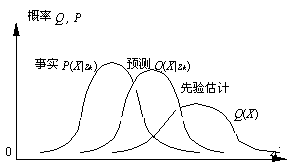
2) 预报员根据气象观察数据和理论(或听众根据预报语言)预测未来某天无雨的概率是主观概率,它有时也被称为可能性测度,后面的Q(xi),Q(xi|Aj)等即是;
3) 给定天气或日降水量时,某一语句比如“这天有大雨”被听众判断为真的概率是逻辑概率,有时也被称之为置信度,后面的Q(Aj|xi),Q(Aj)等即是。
前面两种概率通常被视为概率的两种互不相容解释,自概率论诞生以来就有;而在广义信息论中,这两者是互补的。
值得注意的是,语句yj同时具有客观概率即语句被选择的概率P(yj)和逻辑概率Q(Aj),两者一般不等;前者是纯客观测度,后者和主观理解的语义有关。比如某气象台一年到头总是报“无雨”,则选择概率P(“无雨”)=1,而逻辑概率Q(“无雨”为真)则和“无雨”的语义有关,而和语句被选择与否无关;经验告诉我们,它约为0.8。
P(yj|xi)和Q(Aj|xi),Q(xi|Aj)和P(xi|yj) 的区别同理。
广义通信模型充分体现了这样的思想:信息来自预测,信息的多少需要事实检验;越是把主观原以为偶然的事件预测为必然并且预测正确,信息就越多,否则信息就越少甚至为负值。根据这种思想,最一般的信息是预言信息,其它信息都是预言信息的特例。这一通信模型和波普尔(K. R. Popper)的科学进化模式极为一致;同时也贯彻和深化了马克思主义的实践检验真理思想;Weaver的一些思想也由此得到贯彻。
关于知识或科学理论的进化模式,Popper认为,科学理论起于问题,为了解决问题人们提出假设,理论即假设;假设受到事实检验;如果根据假设所作的预测与事实相符,就说它通过了检验并在某种程度上得到确证;如果与事实不符,它就被证伪了;于是人们又寻求新的更加经得起检验的假说或理论;如此往复,以至科学进化。这种进化和生物进化是类似的。
下面我们介绍和Popper科学理论进化模式相一致的广义通信模型。
假设我们根据已知条件Z和知识K推出客观事件X 发生的概率或可能性分布Qk(X|Z),我们称Qk(X|Z)为主观预测;这一预测通过语句Y间接表达出来。语言可能是自然的,也可能是人工的。再设事件集合A={x1,x2,...,xm},语句集合B={y1,y2,...,yn},观察数据集合C={z1,z2,...,zl};X,Y,Z分别是取值于A,B,C中元素的随机变量。要度量的是Z或Y提供关于X的信息。下面我们用P(X)表示X的概率分布,用P(xi)表示xi或X=xi的概率;其它同理。通信模型如图9.2所示。
我们以降水量预报为例说明该模型:Z表示气象数据,K为气象知识或理论;QK(X|Z)为气象台预测的各种降水量可能性分布(即概率预报)。Y是语句,比如“有小雨”,“有大雨”;Q(X|Y为真)是听众根据语义推出的降水量可能性分布。Q(X)是听众事先根据经验估计的降水量的可能性分布。
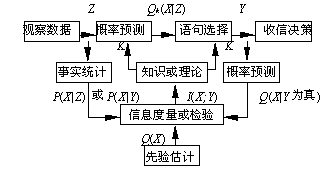
图 .2 广义通信模型
检验知识K和预言Y的方法是看Q(X|Y为真)和Q(X)哪一个更与P(X|Y)相符,若前者更加相符,则预言有正的价值,若后者更加相符,预言价值为负。气象台为了提供更多的信息,于是就一再改进理论或推理方法,试图作出更正确且更精确的预报。如此反复,使预报和事实趋于一致。不光天气预报如此,疾病诊断如此,经济预测如此,各门科学知识的获得和进化也都如此。
由模型可见,最一般的信息是预言信息。下面是模型的几个特例。
广义信息测度有两种形式,一个是概率预测信息,另一个是预言信息。后者可以通过集合Bayes公式转化为前者。首先我们看概率预测信息。
在上面的通信模型中,Z=zk提供的关于xi信息是(后面省去K)
zk提供的关于X的平均信息是:
![]() (9.6.6)
(9.6.6)
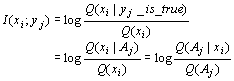 (9.6.8)
(9.6.8)
上式表明:
预言或命题的信息量
=log(命题的逻辑概率/谓词的逻辑概率)该公式将能保证:
模糊集合Aj |
yj(xi) |
Q(Aj) |
Q(Aj|xi) |
评价 |
信息 |
(850点左右) |
“指数将在850点左右” |
0.15 |
1 |
精确 |
2.74 |
(700—1000点} |
“指数将在800—950点” |
0.3 |
1 |
较精确 |
1.73 |
(小于1000) |
“指数是跌的” |
0.5 |
1 |
较模糊 |
1 |
(500—1500点) |
“指数可能涨也可能跌” |
1 |
1 |
极模糊 |
0 |
(大概大于1000点} |
“指数可能是涨的” |
0.6 |
0.6 |
错了 |
- 3.32 |
前面我们假定听者相信语句正确,如果不相信或不完全相信,则我们要用更加模糊的集合代替原来的集合。
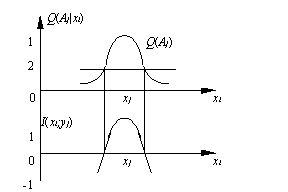
对上式再求平均就得到度量语义信息的广义互信息公式
![]()
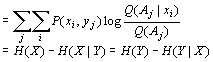 (9.6.10)
(9.6.10)
其中
如果把信息量作为科学理论的进步标准,则我们可以得到如下结论:
信息获取 |
X |
P(Z|X) |
Z |
Y(Z) |
Y=yj=xj |
Q(X|yj为真) |
语言交流 |
客观事实 |
了解方式 |
了解数据 |
语言规则 |
判断语句 |
主观理解 |
感官感知 |
物性(色光) | 感官处理 |
感觉(色觉) | 大脑判断 |
知觉(红) | 认识依据 |
编码通信 |
信源信号 |
编码 |
编码信号 |
解码规则 |
信宿信号 |
行动依据 |
信号检测 |
信源信号 |
有噪信道 |
接收信号 |
检测规则 |
检测值 |
行动依据 |
序列预测 |
t时刻信号 |
前后关系 |
t以前信号矢量 |
预测规则 |
预测值 |
编码或行动依据 |
状态估计 |
t时刻状态 |
前后关系 | t以前状态 |
估计规则 |
估计值 | 控制依据 |
天气预报 |
天气类型 |
观察 |
观察数据 |
预报规则 |
预报语句 |
听众理解 |
股市预测 |
涨跌 |
搜集情报 |
掌握数据 |
预测规则 |
预言 |
股民理解 |
诊断实验 |
疾病类型 |
实验方式 |
实验数据 |
判决规则 |
阴性阳性 |
医生理解 |
化学测试 |
化学成分 |
测试 |
测试数据 |
分析方式 |
分析结果 |
行动依据 |
模式识别 |
不同模式 |
特征抽取 |
特征矢量 |
识别规则 |
模式判断 | 行动依据 |
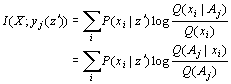 (9.6.15)
(9.6.15)
优化广义通信要解决的问题是:
(详见<<广义信息论>>中国科大出版社出版,邮购:230026合肥中国科大出版社读者服务部,连邮费7元)