1

Investing Channel and Investing Capacity
——Extension of Shannon's Channel Capacity

(Selected from Lu's monograph: Entropy Theory of portfolio and Information Value)

First let us have a look at channel capacity in classical information theory.

For given channel P(Y|X)，mutual information I(X；Y) is different as source H(X) is changed，The channel capacity is defined as：for given channel P(Y|X)，by changing source P(X) -> P*(X) so that mutual information I(X；Y) reaches the maximum. This maximum is channel capacity。Assume P_C is a set of all possible sources. Then capacity C is

(9.4.1)

The channel capacity tells us that we cannot transmit more information than capacity when by limitted channel. In calassical information theory, there is detailed mothed for calculating channel capacity. In the following, we simply introduce Gauss's capacity for noise-splicing channel with normal distribution.

Assume X∈A＝B＝(- ∞，+∞), splicing noise Z is Gauss's variable with average 0 and variance(or power) s ², and input is X and output is Y＝X+Z. We can deduce channel capacity

(9.4.2)

where P_wo and P_wi are output power and input power respectively. The above equation shows that in comparison with input power, the less the noise power s ², the larger the capacity.

Now we consider the problems with investments. We call the pair (P，R), in which P=(P₁，P₂，... P_M) is probability distribution of the vector of future prices, R=(R_ik) is value-increasing matrix, the investing channel. The set q_C formd by all possible vectors , q=(q₀，q₁，q₂，...q_N), of investing ratios. Then the capacity of investing channel (or say investing capacity) is defined as

(9.4.3)

where q* is optimizing investing ratios and is a function of P and R, i.e. q*=q*（R，P）.

For example, in typical gambling, forecasted return is

F_r={0.5|r₁，0.5|r₂}={0.5|D _-，0.5| D ₊)

={0.5|E- R_r，0.5|E+R_r}

which means loss r1=E-Rr and gain r2=E+Rr have equal probability ( where r₁<0<r₂，E is expectation，R_r is new risk measure ). The optimizing ratio is

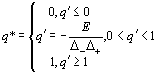(9.4.4)

While q*=q’, the capacity becomes

(9.4.5)

According to Taylor's series-quation, when x<1，

(9.4.6)

Since r₁=E- d <0，E/d <1, and hence there is a approximate formula about investing capacity

(9.4.7)

It can be seen that square of expected return E² is very similar to input power in communication，the square of risk measure R_r² is very similar to noise power. In the above formular, the larger the E²/R_r²，the larger the investing capacity. This is similar to that in communication systems, the larger the ratio of information to noise, the larger the channel capacity.