Based on Incremental Entropy
Abstract Replacing arithmetic mean return and standard deviation adopted by M. H. Markowitz with geometric mean return as criterion of assessing a portfolio, we get incremental entropy: one of generalized entropies. It indicates the increasing speed of capital and is a more objective and testable measure. Most different from Markowitz's theory is that new theory emphasizes that for given probability of returns there is an objectively optimal portfolio ,which can be tested by playing coins or by computer simulation. This paper provides some simple and applicable formulas for optimizing investment ratios and some samples showing the optimization of a portfolio with multi-securities by computer. The paper also presents a information-value measure based on the new portfolio theory, analyses difference and similarity between this measure and K.J. Arrow's information value measure, and discusses how to optimize forecasts with new information-value measure as criterion ,
Keywords: portfolio, criterion of optimization, incremental entropy, information value evaluation and optimization of forecasts
1 IntroductionSeveral years ago, the author presented a generalized information theory, and proved that the generalized information measure also had its coding meaning(Lu,1992,1993,1994). Later, he found that new generalized entropy, i.e. incremental entropy, could be used to optimize portfolios. The new portfolio theory carries on some aspects of Markowitz's theory(1959,1991), but has obvious differences. It emphasizes there is an objective criterion that is incremental speed of capital. On this criterion, for given probability forecast of returns, we can obtain the optimal ratios of investments in different securities or assets. Combining the new portfolio theory and the general information theory, we can approach a meaning-explicit measure of information value, which designates the increment of capital-increasing speed after information is provided while one always makes decision in optimal way. The author has applied the portfolio theory to investments in markets of stocks and futures. The practices show that the theory has obvious superiority. Now, the new theories are presented here for criticisms and discussions.
2 Portfolio Optimization
——Talking about from Gambling with Playing Coins
First of all, we talk about the question of portfolios from a simple sample.Sample 1. Assume there is an investment or bet whose return is uncertain and determined by playing a coin. If A-side appears you will win 200% of your wager and if B-side appears you will lose 100%. You have only 100 dollars and have no way to borrow if you lose . The question is, for many times of the gambling, what ratio of your capital the wager occupies is best so that your capital increases fastest, or say, you become millionaire fastest?
Staking all of your money every time is obvious infeasible because once B-side appears you will lost all of money and the opportunity of your becoming rich forever. Staking 10% of your money is not too bad since you might not lose up forever. After two turns in average your return (yield plus 1) will be (1-1*0.1)(1+2*0.1)=1.08 times. But in this way, whether is the capital-increasing speed too slow? Whether can we find the best investment ratio?
In more general cases, the number of securities or items to be invested in is greater than one, and their future returns are uncertain. For given joint probability distribution of their future returns, how do we determine optimal investment ratios in different securities?
The portfolio theory initiated by Markowitz (1959) has had great achievements. For this reason, M. H. Markowitz, W.F.Shape and M.Miller won 1990's Nobel Prize. The theory tell us that the larger the expected return, the better the investment; the less the standard deviation of return, which means risk, the better; we can reduce the standard deviation of the return or risk by combining anti-covariant securities together. As for how to assess the utility of a portfolio with given expected return and standard deviation, there is no objective criterion, or say, the criterion changes from persons to persons.
The efficient portfolio provided by Markowitz's theory is one that has the smallest risk for a given level of expected return or the largest expected return for a given level of risk. However, it is not a portfolio we need for the fastest increment of capital. So, we need new mathematical method.
3 A Mathematical Model for Portfolios and Derivation of Incremental Entropy
Let the prices of N securities in a portfolio form a N-dimension vector
and the price of the k-th security has nk possible
value, k=1,2,...,N. Hence there are W= ![]() possible price vectors. Assume that the i-th price vector
is
possible price vectors. Assume that the i-th price vector
is ![]() and current price vector is
and current price vector is ![]() ; when the price vector xi happens, the return from the k-th security is rik. Then the return from a portfolio is
; when the price vector xi happens, the return from the k-th security is rik. Then the return from a portfolio is
![]() (3.1)
(3.1)
where qk ,k=1,2,...,N, is
the ratio of capital invested in the k-th security; q0 is the ratio of currency hold by the investor; ![]() ;
; ![]() (1+interest-rate).
Considering the handling charges including tax, then
(1+interest-rate).
Considering the handling charges including tax, then
![]()
where d is handling charges for exchange of each dollar, qk' is the former ratio of the investment in the k-th. security.
Assume that a price vector ri happens Ni times in N experiments of investments; then the return of capital after N experiments of investments is
![]() (3.3)
(3.3)
the average return for each period is
![]() (3.4)
(3.4)
The author understood until recent time that the above mathematical model was first proposed by Henry A.L.atane and Donald L. Tuttle(1967) and was called wealth-maximizing model. However, the following research results in this paper are entirely different from those proposed. One reason is that expectation and standard deviation no longer play important roles.
Taking the logarithmic value and letting N ?8, we have
![]() (3.5)
(3.5)
We call H incremental entropy, which is one of generalized entropies(see Lu, 1993,1994), and has the same metric as information has. It is suggested that we use 2 as the base of the logarithm; then H means the times of doubling capital.
4. Comparing Optimization of Portfolio with that of communication coding In comparison of the generalized entropies(Lu, 1993), the incremental entropy lacks a negative symbol. If let![]() (4.1)
(4.1)
In communication theory, the formula of average coding length is
![]() (4.2)
(4.2)
where ci is coding length for
letter xi; mi is the number of possible codes with length ci. For example, binary numbers 0 and 1 are
used as codes, the base of logarithm is 2; for ci=2,there
are four possible codes:00,01,10,11. Optimization of coding is to change coding rules so
that ![]() reaches its minimum. Shannon's
information theory(1948) tell us that as mi
infinitely approaches 1/P(xi)
for each i,
reaches its minimum. Shannon's
information theory(1948) tell us that as mi
infinitely approaches 1/P(xi)
for each i, ![]() infinitely approaches its
smallest value, which is just Shannon's entropy:
infinitely approaches its
smallest value, which is just Shannon's entropy:
![]() (4.3)
(4.3)
Comparing with (3.5) and (4.1), we can see that ri
matches mi and a vector, (![]() ), of investment ratios matches a coding rule. To
optimize a portfolio is to change (
), of investment ratios matches a coding rule. To
optimize a portfolio is to change (![]() ) so that
H reaches its maximum instead of the minimum.
) so that
H reaches its maximum instead of the minimum.
If a communication channel transmits a code per unit of time and those codes are uncorrelated each other, then H means the speed of information transmission. Similarly, in terms of portfolios, H means the incremental speed of capital. Let rg=2H then rg indicates geometric mean return(GMR). If a portfolio that has incremental multiple rg every year has value M after T years, then
![]() , i.e.
, i.e. ![]() (4.4)
(4.4)
5. Optimization of Investment Ratios In the later, let P(xi) be denoted by Pi ,
 (5.1)
(5.1)
where ![]() means excess return. The q*
can be obtained by solving the above a group of N equations. Since q* is the
function of (Pi ) and (rik ). We
can write q*=q*((
means excess return. The q*
can be obtained by solving the above a group of N equations. Since q* is the
function of (Pi ) and (rik ). We
can write q*=q*((![]() ),(
),(![]() )). When (
)). When (![]() ) is given, ri is the
function of q*; so, we denote ri
corresponding to q* by ri *=ri (q*).
) is given, ri is the
function of q*; so, we denote ri
corresponding to q* by ri *=ri (q*).
Considering the question of optimizing investment ratio in the front of the paper. In that case N=1, i=1,2, Formula (5.1) becomes
![]() (5.2)
(5.2)
where P1 , P2 are probabilities in which A-side and B-side appears
respectively, q is the investment ratio, ![]() and
and ![]() are the rate of loss and
gain minus interest rate respectively. From (5.2),we can derive optimal ratio
are the rate of loss and
gain minus interest rate respectively. From (5.2),we can derive optimal ratio
![]()
![]() (5.3)
(5.3)
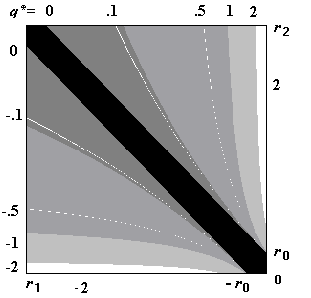
Fig. 4.1 Showing relationship between q* and r1,r2,r0
Note the numerator is just the expectation of the excess return. Put ![]() ,
,![]() =1
into the above formula, we have q*=0.25. It is said that the optimal investment
ratio is 25%. The return will be (1-1*0.25)(1+2*0.25) =1.125 times in average after every two turns. If
=1
into the above formula, we have q*=0.25. It is said that the optimal investment
ratio is 25%. The return will be (1-1*0.25)(1+2*0.25) =1.125 times in average after every two turns. If ![]() and
and ![]() are
both greater or less then 0, the above formula is not suitable. In these cases q*
should be equal to 1 or -1 if overdraft is not allowable.
are
both greater or less then 0, the above formula is not suitable. In these cases q*
should be equal to 1 or -1 if overdraft is not allowable.
From (3.3) we can get a interesting conclusion. Let ![]() , r0 =1; then
, r0 =1; then
![]() (5.4)
(5.4)
which means that when gain and loss are equally possible, if the loss might be up to 100% then do not stake more than 50% of your fund no matter how high the possible gain may be. This conclusion is very meaningful to investments in futures, options, and the like. Many new comers of future markets lose all of their money very fast because the investment ratios are not well controlled and generally too large.
From (5.3), q* >1 and q* <0 are possible. The q*>1 means that you had better skate 100% or q*=100%, if lending or overdraft is allowable, of your capital. The q*<0 means that you had better skate nothing or |q*|=100% on oversale if it is allowable.
For a security with possibility of multi-returns, we can use computer to obtain optimal ratios on (3.5), and can also adopt approximate formulas. One is
(omitted)
6. Affection of Covariance on Geometric Mean Return (GMR) from the Point of New Theory
The affection of covariance of returns of securities on the investment value of a portfolio has be well discussed by Markowitz(1959,1991). Now we explain that by the new theory we can reach similar conclusions and how we reduce risk and improve incremental speed of capital by optimizing investment ratios.
Sample 2. Let the excess return of a future investment be represented by two sides of a couple of coins. You win 300% if two coins show A sides, you lose 200% if two coins show B sides, and you win 100% if two coins show different sides. Assume there are two futures whose returns are determined as above; but probably one or two coins are commonly used. Calculate the geometric mean returns as you invest all capital(50% for each) and invest in optimal ratios.
Table 2 shows the results, in which
Table 2. Affection of covariance on geometric mean return and optimized results(data in brackets are approximately optimal results from (5.8))
(omitted)
It is obvious that the larger the covariance coefficient, the worse the effect of portfolio. The covariance coefficient 1 means that two securities become one so that loss is great. The less the covariance coefficient, the better the effect. The covariance coefficient -1 results in the best effect so that the geometric mean return is equal to the arithmetic mean return. The data in the right two columns of Table 2 show that we can improve geometric mean return by properly reducing investment ratios especially in case of that great risk exists.
7 In Comparison with Markowitz's Theory
The new theory supports Markowitz 's conclusions about reducing investment risk by effective portfolio. Different is that
1)The new theory refers to geometric mean return as objective criterion for optimizing portfolio and provides optimal investment ratios for the fastest increment of capital in a long term;
2)The new theory employs extents and possibilities of gain and loss or utility function u=u(q) instead of expectation and standard deviation of return as description of investment value of a security or a portfolio.
Sample 3. Current prices of two securities A and B are both 1 (dollar); possible prices of A in future is 0 and 2 with probability 1/4 and 3/4; the price of security B in future has the same expectation (1.5) and standard deviation (0.886) but mirrored probability distribution. The analyses of investment values of the two securities is shown in Table 3, in which bank-interest is neglected.
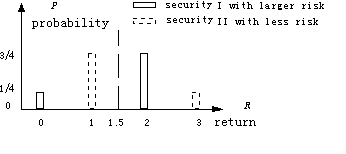
Table 3
| expectation | Standard variance | Average compound interest when Staking 100% | Optimizing ratio | Average compound interest after optimization | |
| Security I | 0.5 | 0.886 | -100% | 50 | 15% |
| Security II | 0.5 | 0.886 | 32% | >=100 | >=32% |
The optimal ratio q*>=100% means that if overdraft is allowable, you had better overdraw to buy and the more you overdraw, the better. On Markowitz 's theory, A and B have the same investment value; but on the new theory, B is much better than A. For investments with possibility of loss in large proportion, such as option, future, loan, and insurance sale, the above defect in Markowitz 's theory is clearer.
8 Information Value Formula Based on Incremental Entropy
In the generalized information theory( Lu, 1993), probability is distinguished into subjective probability, which is subjectively forecasted by somebody, objective probability, in which a event actually happens, and logical probability. Logical probability of a prediction or a proposition is also called confidence level, it takes a value from real interval [0,1].Assume X is a random variable taking a value from a event set ![]() and Y is a random variable taking a value
from a proposition set
and Y is a random variable taking a value
from a proposition set ![]() ; Y transmits
information about X.. Events that make a proposition yj be true form a subset Aj ,which is a fuzzy set because logical probability of yj as feature function of Aj take a value from [0,1]. Information about xi and average information about X transmitted
by yj is
; Y transmits
information about X.. Events that make a proposition yj be true form a subset Aj ,which is a fuzzy set because logical probability of yj as feature function of Aj take a value from [0,1]. Information about xi and average information about X transmitted
by yj is
![]() (8.1)
(8.1)
![]() (8.2)
(8.2)
where ![]() is objective probability, Q(xi) is prior subjective probability and
is objective probability, Q(xi) is prior subjective probability and ![]() is posterior subjective probability deduced from yj. If yj
is made on observed datum Z=z', then average information is
is posterior subjective probability deduced from yj. If yj
is made on observed datum Z=z', then average information is
![]() (8.3)
(8.3)
Given a vector probability distribution q=(Q![]() )=Q(X) and a return matrix (
)=Q(X) and a return matrix (![]() ), we assume P(X)= Q(X) to
obtain optimal investment ratio vector q*=q*((Q
), we assume P(X)= Q(X) to
obtain optimal investment ratio vector q*=q*((Q![]() ),(
),(![]() )) by (3.5). With the forecast changes from (Q
)) by (3.5). With the forecast changes from (Q![]() ) into (
) into (![]() )=
)=![]() , q*
becomes q**=q**((
, q*
becomes q**=q**((![]() ),(
),(![]() )). We define the increment of the incremental
entropy after information is provided as information value:
)). We define the increment of the incremental
entropy after information is provided as information value:
![]() (8.4)
(8.4)
It can be seen that ![]() and
and ![]() have similar mathematical construction.
Information value of yj as xi certainly happens is
have similar mathematical construction.
Information value of yj as xi certainly happens is
![]() (8.5)
(8.5)
Both information and information value are relative and especially depend on how an
information receiver understands a prediction. The relativity of information value is also
due to the return matrix (![]() ) is different to
different investors with different limits of investing tools. The asymmetry of information
and information value comes from the same reasons.
) is different to
different investors with different limits of investing tools. The asymmetry of information
and information value comes from the same reasons.
9 In Comparison with Arrow 's Formula of Information Value
Arrow defined information value or information utility as increment of utility after information is provided(1984). The utility function is
![]() (9.1)
(9.1)
where ri denotes the i-th
return of a investment or a gambling; Pi
is corresponding probability; ai is
the ratio of capital invested or skated in the i-th return, instead of security; ![]() is the utility obtained by the investor when the
i-th return happens. Logarithmic function is employed because Arrow thought of that
logarithmic function as utility function was reasonable, without considering geometric
mean return.
is the utility obtained by the investor when the
i-th return happens. Logarithmic function is employed because Arrow thought of that
logarithmic function as utility function was reasonable, without considering geometric
mean return.
Under the limit ![]() , U reaches its
maximum as (ai)=(Pi ). The maximum is
, U reaches its
maximum as (ai)=(Pi ). The maximum is
![]() (9.2)
(9.2)
After information is provided, the investor knows which return will exactly happen and hence invests all capital in this return. Then
![]() (9.3)
(9.3)
The information value is just Shannon's entropy, i.e.
![]() (9.4)
(9.4)
The Arthur's definition of information value carries on Arrow's thought: 1)for given
forecast of returns, there is an objective optimal investment ratio; 2)information value
is equal to the increment of utility after information is provided. However, the
investment model employed in this paper is very different. From the author's view-point,
the investment model employed by Arrow is very strange. We can invest in a security or a
item; but how can we invest in some return of a security or a item? Equation (9.1) demands
each ![]() is positive, which means investments
with possible loss are not allowable, since the logarithm of a negative number is
meaningless. Is this investment or gambling common as we see in daily life? Arrow 's model
might be suitable to the game of guessing stock index for award, which is generally
organized by newspaper seller. But it is still hard to understand that
is positive, which means investments
with possible loss are not allowable, since the logarithm of a negative number is
meaningless. Is this investment or gambling common as we see in daily life? Arrow 's model
might be suitable to the game of guessing stock index for award, which is generally
organized by newspaper seller. But it is still hard to understand that ![]() <1 results in negative utility. It is these
reasons that the application of Arrow 's formula of information value is difficult.
<1 results in negative utility. It is these
reasons that the application of Arrow 's formula of information value is difficult.
10 Applying New Measure of Information Value to Assessments of Forecasts
Formula (8.4) can be used to optimize forecasts. Let ![]() . Given (Pi ), we seek
probability forecast Q(X| yj
=y*) that makes
. Given (Pi ), we seek
probability forecast Q(X| yj
=y*) that makes ![]() reach its maximum;
then y* is optimal prediction. It is not difficult to prove that when (
reach its maximum;
then y* is optimal prediction. It is not difficult to prove that when (![]() )=(Pi
), or say, the prediction is accurate,
)=(Pi
), or say, the prediction is accurate, ![]() and
and ![]() reach their maximums at the same time. If
prediction set B is limited so that there is no prediction that makes (
reach their maximums at the same time. If
prediction set B is limited so that there is no prediction that makes (![]() )=(Pi
). In this case, the prediction that makes (
)=(Pi
). In this case, the prediction that makes (![]() )
most close to (Pi ) is optimal
prediction.
)
most close to (Pi ) is optimal
prediction.
Sample 4 A stock index X takes a value from the set A=[100,110,120,130,...].
A set of predictions about X is B={ yj
="X is about to be xj
"| j=1,2,...}. The logical probability of yj
or the membership grade of xi in Aj is ![]() ; for example, it is hill-like function with xj
as its center and
; for example, it is hill-like function with xj
as its center and ![]() as its standard
deviation:
as its standard
deviation:
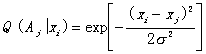 (10.1)
(10.1)
Current stock index is x0 . The prior probability forecast is Q(X),such as a normal distribution function with x0 as the center; yet fact happens in objective probability P(X|z'). Please calculate information value of prediction yj ="X is about to be xj " and optimal prediction y*.
Solution. On generalized Bayesian formula(Lu,1993), we have
![]() (10.2)
(10.2)
in which Q( Aj ) means logical probability of predicate yj (.) and
Q( Aj )=![]() (10.3)
(10.3)
From the incremental entropy
![]() (10.4)
(10.4)
we obtain optimal ratio q*; from the incremental entropy
![]() (10.5)
(10.5)
we obtain optimal ratio q**. The information value of yj is hence
![]() (10.6)
(10.6)
For each yj in B, we can
have corresponding q**. The yj that
makes information value ![]() or posterior
incremental entropy
or posterior
incremental entropy
![]() (10.7)
(10.7)
reach the maximum is optimal prediction y*.
11 Summary
This paper has provided applicable the theory of portfolio and information value based on incremental entropy, in which some fundamental thoughts of Markowitz and Arrow are carried on. From the author's view-point, as for investment model, Markowitz is correct yet Arrow is wrong; but as for if there is objectively optimal investment ratio for given probability forecast of returns, Arrow is correct yet Markowitz is wrong . This paper is expected to have advantages of the two theories and to unify the theory of portfolio and that of information value that seem independent each other on higher level.
The author has finished a software for simulating portfolio and testing optimal ratios by repeated investments. The software can calculate optimal investment ratios from probability forecast of returns of several securities and matrix of covariance coefficients of the returns. Running the software shows that the more times the investments are repeated, the clearer the ascendancy of computer is; the greater the risk is or the more complicated the covariance is, the clearer the ascendancy of computer is. Further research of the applications is proceeding. Welcome to common explorations.
References
Arrow,K.J.1984: The Economics of Information, Basil Blackwel Limited.
Latane, H. A. and Tuttle D. L., 1967: Criterion for portfolio building, The Journal of Finance, 22(3),359- 373.
LU, Chen-Guang, 1992: Applying a generalized information theory to assessment and optimization of forecasts, Forecasts, 12(3), 54-57.
LU,Chen-Guang, 1993: A Generalized Information Theory, China Science and Technology University Press.
LU,Chen-Guang, 1994: Coding meanings of the generalized entropies and generalized mutual information, Journal of China Institute of Communications, 15(6), 37-44.
Markowitz, M.H.1959: Portfolio Selection, Efficient Diversification of Investments, Yale University Press
Markowitz, M.H 1991: Foundations of Portfolio Theory, The Journal of Finance, 46(2), 469-477
Shannon,C.E., 1948: A mathematical theory of communication, Bell System Technical Journal, 27, 379-429 and 623-656.