Abstract--With
help of fish-covering model, this paper intuitively explains how to extend Hartley’s information formula to the generalized
information formula step by step for
measuring subjective information: metrical information (such as conveyed
by thermometers), sensory information (such as conveyed by color vision), and
semantic information (such as conveyed by weather forecasts). The pivotal step
is to differentiate condition probability and logical condition probability of
a message. The paper illustrates the rationality of the formula, discusses the
coherence of the generalized information formula and Popper’s knowledge
evolution theory. For optimizing data compression, the paper discusses
rate-of-limiting-errors and its similarity to complexity-distortion based on
Kolmogorov’s complexity theory, and improves the rate-distortion theory into
the rate-fidelity theory by replacing Shannon’s distortion with subjective
mutual information. It is proved that both the rate-distortion function and the
rate-fidelity function are equivalent to a rate-of-limiting-errors function
with a group of fuzzy sets as limiting condition, and can been expressed by a
formula of generalized mutual information for lossy coding, or by a formula of
generalized entropy for lossless coding. By analyzing the rate-fidelity
function related to visual discrimination and quantizing bits of pixels of images,
the paper concludes that subjective information is less than or equal to objective
(Shannon’s) information; there is an optimal matching point at which two kinds
of information are equal; the matching information increases with visual discrimination
(defined by confusing probability) rising; for given visual discrimination, too
high resolution of images or too much objective information is wasteful.
Index Terms--Shannon’s
theory, generalized information theory, subjective information, metrical
information, sensory information, semantic information, Popper’s theory,
complexity-distortion, rate-distortion, rate-fidelity.
I.
Introduction
To measure sensory information and semantic
information, I set up a generalized information theory thirteen years ago [4-8]
and published a monograph focusing on this theory in 1993 [5]. But, my researches
are still rarely known by English researchers of information theory. Recently,
I read some papers about complexity distortion theory [2], [9] based on
Kolmogorov’s complexity theory. I found that, actually, I had discussed
complexity-distortion function and proved that the generalized entropy in my
theory was just such a function, and had concluded that the complexity-distortion
function with size-unequal fuzzy error-limiting balls could be expressed by a
formula of generalized mutual information. I also found that some researchers did
some efforts [9] similar to mine for improving Shannon’s rate-distortion theory.
This paper first explains how to extend Hartley’s
information formula to the generalized information formula, and then discusses the generalized mutual
information and some questions related to Popper’s theory, complexity
distortion theory, and rate-distortion theory.
II. Hartley’ s Information Formula and a
Story of Covering Fish
Hartley’s information formula is [3]
I=logN,
(1)
where I denotes the information
conveyed by the occurrence of one of
N events with
equal probability. If a message y tells that uncertain extension changes
from N1 to N2,
then information conveyed by y is
Ir=I1-I2=logN1-logN2=log(N1/N2).
(2)
We call (2) relative information formula. Before
discussing its properties, I tell a story about covering fish with fish covers.
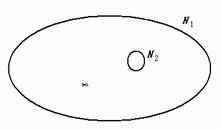
Figure 1. Fish-covering model for relative information
Ir
Fish covers are made of bamboo. A fish cover looks
like a hemisphere with a round hole at top for human hand to catch fish. Fish
covers are suitable for catching fish in adlittoral pond. When I was a teenage,
after seeing peasants catch fish with fish covers, I found a basket with a hole
at bottom and followed those peasants to catch fish. Fortunately, I
successfully caught some fish. Then I compared my basket with much bigger fish
covers to concluded that the fish cover is bigger so that covering fish is
easier; yet, catching fish with hand is more difficult; if a fish cover is big
enough to cover the pond, it must be able to cover fish; yet, it is useless
because catching fish with hand is the same difficult as before; when one uses
the basket or smaller fish cover to cover fish, though covering fish is more
difficult, catching fish with hand is much easier.
An uncertain event is alike a fish with random position
in a pond. Let a sentence y=” Fish is covered”; y will convey
information about the position of fish. Let N1 be the area of
the pond, N2 be the area covered by the fish cover, then
information conveyed by y is Ir=log( N1/
N2). The smaller N2
is than N1,
the bigger the information amount is. This just reflects the advantage of the
basket. If N2= N1，then I=0. This just tells us that covering fish is
meaningless if the cover is the same big as the pond. As for the advantage of
fish covers (with less failure) in comparison with the basket, the above formula
cannot tell because in the classical information theory, there seems a
hypothesis that the failures of covering fish never happen.
III.
Improving the Fish-covering Formula with Probability
Hartley’s information formula requires N
events with equal probability P=1/N. Yet, the probabilities of
events are unequal in general. For example, the fish stays in deep water in
bigger probability and in shallow water in smaller probability. In these cases,
we need to replace 1/N with probability P so that
I=log(1/P)
(3)
and
Ir =log(P2/ P1).
(4)
IV. Relative Information Formula with a Set as Condition
Let X denote the random variable taking
values from set A={x1, x2,
…} of events, Y denote the random variable taking values from set B={y1,
y2,…} of sentences or messages. For each yj,
there is a subset Aj
of A and yj =“xi ∈Aj ”, which can be cursorily understood as “Fish
xi is in cover Aj ” . Then P1 above becomes P(xi), P2 becomes P(xi|xi ∈Aj). We simply denote P(xi|xi
∈Aj) by
P(xi|Aj), which is
conditional probability with a set as condition. Hence, the above relative information
formula becomes
. (5)
For convenience, we call this
formula as the fish-covering information formula.
Note that the most important
thing is generally P(xi|Aj)
≠P(xi |yj), because
P(xi|yj)= P(xi|“xi
∈Aj”)=P(xi |“xi
∈Aj” is reported);
yet,
P(xi|Aj)=
P(xi|xi ∈Aj)=P(xi |“xi
∈Aj” is true),
where yj may be an incorrect reading
datum, a wrong message, or a lie, yet, xi ∈Aj means that yj must be correct. If they are
always equal, then formula (5) will become classical information formula
, (6)
whose average is just Shannon mutual
information [11].
V. Bayesian
Formula for the Fish-covering Information Formula
Let the feature function of set Aj be Q(Aj|xi)
∈{0,1}.
According to Bayesian formula, there is
P(xi |Aj)=Q(Aj
| xi )P(xi )/Q(Aj
),
(7)
where
. From (5) and (7), we have
, (8)
which (illustrated by Figure 2) is the
transition from classical information formula to generalized information
formula.
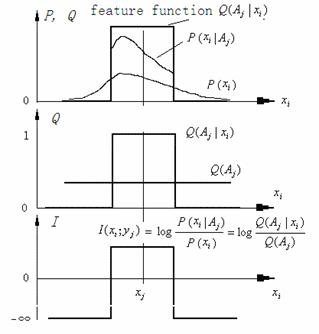
Figure 2. Illustration of fish-covering information
formula related to Bayesian formula
The reading datum of a thermometer may be considered
as reporting sentence yj∈B={y1, y2,…}，and real temperature as the fish position xi
∈A={x1, x2,
…}. Let yj =“xi ∈Aj”, and Aj = [xj-△x, xj+△x]
according to the resolution of the thermometer and eyes' visual discrimination.
Hence, we can use the fish-covering information formula to measure thermometric
information.
VI. Generalized Information Formula with
a Fuzzy Set as Condition
Information conveyed by a reading datum of thermometer
and information conveyed by a forecast “The rainfall will be about 10 mm” are
the same in essence. Using a clear set as condition as above is not good enough
because the information amount should change with xi
continuously. We wish that the bigger the error (i.e. xi-xj
), the less the information. Now, using a fuzzy set to replace the clear set as
condition, we can realize this purpose (see Figure 4).
Now, we consider yj as sentence “X
is xj ” (or say
yj =
). For a fuzzy
set Aj whose feature function Q(Aj|xi)
takes value from [0, 1] and Q(Aj|xi)
can be considered as confusing probability of xi with xj. If i=j,
then the confusing probability reaches its maximum 1.
Actually, the confusing probability Q(Aj|xi)
is only different parlance of the membership grade of xi in fuzzy
set Aj or the logical probability of proposition yj
(xi). There is
Q(Aj|xi)=feature
function of Aj
=confusing probability or similarity of xi
with xj
=membership grade of xi in Aj
=logical probability or creditability of proposition yj(xi
)
The discrimination of human sense organs, such as visual
discrimination for gray levels of pixels of images, can also be described by confusing
probability functions. In these cases, a sensation can be considered as a
reading datum yj=of the thermometer. The visual discrimination function of xj
is Q(Aj|xi), i=1, 2,… where Aj
is a fuzzy set containing all xi that are confused with xj.
We may use the statistic of random clear sets to obtain this function [13] (see
Figure 3).
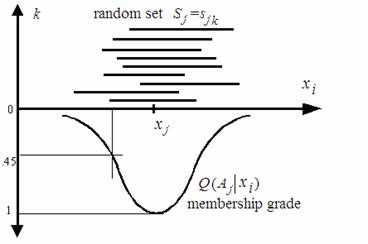
Figure 3 Confusing probability function from clear
sets
First we do many times experiments to get the clear sets sjk, k=1,
2, …, n, by putting xj on one side of a screen, xi
on another side of the screen. And then we calculate
(9)
Now, replacing a clear set with a fuzzy set as
condition, we get the generalized information formula:
(10)
It looks the same as the fish-covering information
formula (8), but Q(Aj|xi)
∈[0,1]
instead of Q(Aj|xi) ∈{0,1}.
And also, this formula allows wrong reading data or messages, bad forecasts, or
lies which convey negative information. The generalized information formula can
be understood as fish-covering information formula with fuzzy cover. Because of
fuzziness, generally, negative information amount is finite. The property of
the formula can be illustrated by Figure 4.
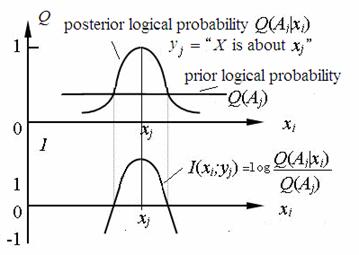
Figure 4
Generalized information formula for measuring metrical information, sensory
information, and number-forecasting information
Figure 4 tells us that when a reading datum or a
sensation yj= is provide, the bigger the difference of xi
from xj, the less the information; and the less the Q(Aj),
the bigger the absolute value of information. From this formula, we can
conclude that information amount is also not only depends on the correctness of
reflection, but also depends on the precision of reflection.
VII.
Coherence of the Semantic Information Measure and Popper’s Criterion of Advance
of Knowledge
The generalized information formula can also be used
to measure semantic information in general, such as information from weather
forecast “Tomorrow will be rainy or heavy rainy”. We may assume that for any proposition yj,
there is a Plato’s idea xj which makes Q(Aj|xj)=1.
The idea xj is probably not in Aj. Hence,
any logical condition probability Q(Aj|xi)
can be considered as the confusing probability of xi with the
idea xj.
From my view-point, forecasting information is more
general information in comparison with descriptive information. If a forecast
is always correct, then the forecasting information will become descriptive
information.
About the criterion of advance of scientific theory, philosopher
Karl Popper wrote:
“The criterion of relative potential satisfactoriness…
characterizes as preferable the theory which tell us more; that is to say, the
theory which contains the greater amount of empirical information or content;
which is logically strong; which has the greater explanatory and predictive
power; and which can therefore be more severely tested by comparing predicted
facts with observations. In short, we prefer an interesting, daring, and highly
informative theory to a trivial one.” ( in [10], pp. 250)
Clearly, Popper used information as the criterion to
value the advance of scientific theories. According to Popper’s theory, the
more easily a proposition is falsified logically and the more it can go through
facts (in my words, the less the prior logical probability Q(Aj)
is, and the bigger the posterior logical probability Q(Aj|xi)
is ), the more information it conveys and the more meaningful it is. Contrarily,
a proposition that can not be falsified logically (in my words, Q(Aj|xi)＝Q(Aj)＝1) conveys no information and is insignificant in
science. Obviously, the generalized information measure is very coherent with Popper’s
information criterion; the generalized information formula functions as a bride
between Shannon’s information theory and Popper’s knowledge evolution theory.
VIII．Generalized Fullback’s Information
and Generalized Mutual Information
Calculating the average of I(xi;
yj) in (10), we have generalized Fullback’s information formula
for given yj:
. (11)
Actually, the probabilities on right of log should be
prior probabilities or logical probabilities, the probability on left of log
should be posterior probability. Since now we differentiate two kinds of
probabilities and use Q(.) for those probabilities after log. Hence the above
formula becomes
. (12)
We can prove that as Q(X|Aj)=
P(X|Aj), which means subjective probability forecasts conforms
to objective statistic, I(X; yj) reaches its
maximum. The more different the Q(X) is from P(X|Aj),
which means that the facts are more unexpected, the bigger the I(X;
yj) is. This formula also conforms to Popper’s theory.
Further, we have generalized mutual information
formula
(13)
where
(14)
(15)
(16)
(17)
I call H(X) forecasting entropy, which
reflects the average coding length when we economically encode X according
to Q(X) while real source is P(X), and reaches its
minimum as Q(X)= P(X). I call H(X|Y) posterior
forecasting entropy, call H(Y) generalized entropy, and call H(Y|X) generalized condition entropy or fuzzy
entropy [6].
I think that the generalized information is subjective
information and Shannon information is objective information. If two weather
forecasters always provide opposite forecasts and one is always correct and
another is always incorrect. They convey the same objective information, but
the different subjective information. If Q(X)= P(X) and Q(X|Aj)= P(X|yj)
for each j, which means subjective forecasts conform to objective facts,
then the subjective mutual information equals objective mutual
information.
IX. Rate-of-limiting-errors and Its Relation
to Complexity-distortion
In [5], I defined rate-of-limiting-errors, which is
similar to complexity distortion [2]. The difference is that the error-limiting
condition for rate-of-limiting-errors is a group of sets or fuzzy sets AJ=
{ A1, A2…}
instead of a group of balls with the same size and clear boundaries for
complexity distortion.
We know that the color space of digital images is
visually ununiform and human eyes’ discrimination is fuzzy. So, in some cases,
such as coding for digital images, using size-unequal balls or fuzzy balls as
limiting condition will be more reasonable.
Assume P(Y) is a source; encode Y
into X; allow yj is encoded into any xj
in clear set Aj, j=1, 2…; then the minimum of Shannon
mutual information for different P(X|Y) is defined as rate-of-limiting-errors R(AJ).
I had proved that R(AJ)= H(Y).
To realize this rate, there must be P(X|yj)= Q(X|Aj)
for each j [5].
Furthermore, when the limiting sets are fuzzy, i.e. P(X|yj)
≤ Q(X|Aj) for each j as Q(Aj|xi)<1,
there is
(18)
To realize this rate, there must be P(X)= Q(X)
and P(X|yj)= Q(X|Aj) for each
j so that Shannon’s mutual information equals the generalized mutual
information.
Now, from the view-point of the complexity distortion
theory, the generalized entropy H(Y) is just prior complexity,
the fuzzy entropy H(Y|X) is just the posterior complexity,
and I(X;Y) is the reduced complexity.
X. Rate Fidelity Theory: Reformed Rate Distortion Theory
Actually, Shannon ever mentioned fidelity criterion
for lossy coding. He used the distortion as the criterion for optimizing lossy
coding because the fidelity criterion is hard to be formulated. However, distortion is not a good criterion
in most cases.
How do we value a person? We value him according to
not only his errors but also his contributions. For this reason, I replace the error
function dij=d(xi, yj)
with generalized information Iij= I(xi;
yj) and distortion d(X, Y) with
generalized mutual information I(X; Y) as criterion to
search the minimum of Shannon mutual information Is(X;
Y) for given P(X)=Q(X) and the lower limit G of I(X; Y). I call this criterion the fidelity criterion, call the minimum
the rate-fidelity function R(G), and call the reformed theory the
rate fidelity theory.
In a way similar to that in the classical information
theory [1], we can obtain the expression of function R(G) with
parameter s:
(19)
where s=dR/dG indicates the
slope of function R(G) ( see Figure 5) and
.
We define a group of sets BI= {B1, B2…}, where B1, B2… are subset of B={y1, y2,…},
by fuzzy feature function
(20)
where m is the maximum of exp(sIij);
then from (19) and (20) we have
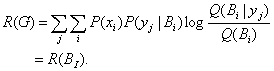(21)
This function is just the rate-of-limiting-errors with
a group of fuzzy sets BI={B1, B2…} as limiting
condition while coding X in A into Y in B. From
this formula, we can find there is profound relationship between
rate-of-limiting-errors and rate-fidelity (or rate-distortion). In the above
formulas, if we replace Iij with dij=d(xi,
yj), (21) is also tenable. So, actually rate-distortion
function can be expressed by a formula of generalized mutual information.
In [7], I defined information value V by the increment of growing speed of
fund because of information, and
suggested to use the information value as criterion to optimize communication
in some cases to get function rate-value R(V), which is also meaningful.
XI.
Rate-fidelity Function for Optimizing Image Communication
For simplicity, we consider how subjectively visual
information is related to visual discrimination and quantizing grades of gray
levels of pixels of images,.
Let the gray level of quantized pixel be a source and
the gray level is xi=i, i=0, 1... b =2k
-1 with normal probability distribution whose expectation=b/2 and standard
deviation= b/8 (see [4] for details). Assume that after decoding the
pixel also has gray level yj=j=0, 1... b; the
perception caused by yj is also denoted by yj;
and discrimination function or confusing probability function of xj is
(22)
where d is discrimination parameter.
The smaller the d, the higher the discrimination.
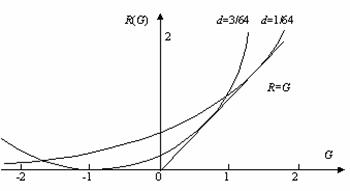
Figure 5
Relationship between d and R(G) for b=63
Figure 5 indicates that when R=0, G<0,
which means that if a coded image has nothing to do with the original image, we
still believe it reflects the original image, then the information will be
negative. When G=-2, R>0, which means that certain objective
information is necessary when one uses lies to deceive enemy to some extent; or
say, lies based on facts are more terrible than lies based on nothing. The each
line of function R(G) is tangent with the line R=G,
which means there is a matching point at which objective information is equal
to subjective information, and the higher the discrimination (the less the d),
the bigger the matching information amount. The slope of R(G)
becomes bigger and bigger with G increasing, which tell us that for
given discrimination, it is limited to increase subjective information.
Figure 6 tells us that for given discrimination, there
exists the optimal quantizing-bit k' so that the matching value of G
and R reaches the maximum. If k<k', the matching
information increases with k; if k>k', the
matching information no longer increases with k. This means that too
high resolution of images is unnecessary or uneconomical for given visual
discrimination.
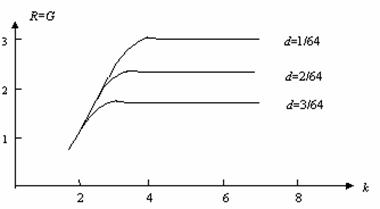
Figure 6
Relationship between matching value of R with G,
discrimination parameter d, and quantizing bit k
XII. Conclusions
This paper has deduced
generalized information formula for measuring subjective information by
replacing condition probability with logical condition probability, and
improved the rate-distortion theory into the rate fidelity theory by replacing
Shannon distortion with subjective mutual information. It has also discussed
the rate-fidelity function related to visual discrimination and quantizing
grades of images, and gotten some meaningful results.
References
[1] T. Berger, Rate Distortion Theory,
Englewood Cliffs, N.J.: Prentice-Hall, 1971.
[2] M. S. Daby and E. Alexandros,
“Complexity Distortion Theory”, IEEE Tran. On Information Theory, Vol.
49, No. 3, 604-609, 2003.
[3] R. V. L. Hartley, “Transmission of
information”, Bell System Technical Journal, 7 , 535, 1928.
[4] C.-G. Lu, “Coherence between the
generalized mutual information formula and Popper's theory of scientific
evolution”(in Chinese), J. of Changsha University, No.2, 41-46, 1991.
[5] C.-G. Lu, A
Generalized Information Theory (in Chinese), China Science and Technology
University Press, 1993
[6] C.-G. Lu, “Coding meaning of generalized
entropy and generalized mutual information” (in Chinese), J. of China
Institute of Communications, Vol.15, No.6, 38-44, 1995.
[7] C.-G. Lu, Portfolio’s Entropy Theory
and Information Value, (in Chinese),
China Science and Technology University Press, 1997
[8] C.-G. Lu, “A generalization of Shannon's
information theory”, Int. J. of General Systems, Vol. 28, No.6, 453-490,
1999.
[9] G. Peter and P. Vitanyi, Shannon
information and Kolmogorov complexity, IEEE Tran. On Information Theory, submitted, http://homepages.cwi.nl/~paulv/papers/info.pdf
[10] K. Popper, Conjectures
and Refutations—the Groth of Scientific Knowledge, Routledge, London and
New York, 2002.
[11] C. E.
Shannon, “A mathematical theory of communication”, Bell System Technical
Journal, Vol. 27, pt. I, pp. 379-429; pt. II, pp. 623-656, 1948.
[12] P. Z. Wang, Fuzzy Sets and Random Sets Shadow
(in Chinese), Beijing Normal University Press, 1985.