4.       CODING MEANINGS

The objectivity of the generalized entropy and the generalized mutual information may be examined by a discussion on their coding meanings. 

4.1       The coding Meaning of the Probability-forecasting Entropy H(X)

 Theorem 4.1.1 Assume a distortionless coding for past or forecasted source Q(X) making the average coding length L approach Shannon’s entropy:

  H_Q(X)= - Q(x_i)logQ(x_i).   (21)

The coding makes

 H_Q(X)£ L£ H_Q(X) +e

possible, where e is an arbitrarily small positive number (the coding must be possible according to one of Shannon's coding theorems), then this coding for actual source P(X) can make the average code length approach the probability forecasting entropy H(X) (defined by Equation (18)).

Proof  Let L_i be the code length of x_i, then the average code length is

L= Q(x_i)L_i.         

Comparing this equation with Shannon's distortionless coding theorem of discrete memoryless source, we have

   L_i= - logQ(x_i)+e_i,

  where e_i makes

        Q(x_i)e_i=e.

  Hence when coding actual source P(X), the average code length is

  L'= P(x_i)L_i=H(X)+ P(x_i)e_i,

  which approaches H(X).   Q.E.D.

 With the inequality logx £ x-1, we can prove that H(X) is greater than or equal to Shannon's entropy of actual source P(X) ( Aczel and Forte 1986).  Therefore,  the more consistent Q(X) is to P(X), the shorter the average coding length is.

4.2      The Coding Meaning of the Generalized Mutual Information

 Theorem 4.2.1 When the forecast Q(X|A_j ) for  j=1, 2, ..., n  might be inconsistent with the fact P(X|y_j ), we code X according to the forecast, then the average code length can infinitely approach the generalized condition entropy H(X|Y) as defined by Equation (20) (the proof is similar to the proof for Theorem 4.1.1).

 We code X according to Q(X) before receiving the information so that the average code length  is close to H(X), and code X according to Q(X|A_j ) for j=1, 2, ..., n after receiving the information so that the average code length is close  to H(X|Y). Obviously, the saved average code length  is close  to the generalized mutual information I(X;Y)=H(X)-H(X|Y). Note that if the forecast always conforms with the fact, then the average code length for the given forecast can infinitely approach Shannon's condition entropy and hence the saved average code length is Shannon's mutual information.

 The negative infinite information means that if one codes X according to a wholly false forecast, the increment of average code length will be infinitely long. The coding meaning of the generalized mutual information is further  examined in the following sections.

4.3       Rate-of-limiting-errors and Coding Meaning of the Generalized Entropy

 In the classical information theory, rate-distortion function R(D) is defined as

    (22)

  where D is the upper limit of average distortion; I_s(X;Y) is Shannon’s mutual information, which is the function of source P(X) and channel P(Y|X);  P_D is the set of all possible channels that make the average distortion

  ,  (23)

  in which d_ij ³0 is the distortion of y_j  corresponding to x_i. The function R(D) means the shortest average code length when communication quality is limited by D. This is the basis of modern theory of data compression.

 Definition 4.3.1 Let P(Y) be a source and P(X) be a destination (contrarily).  Clear sets A₁, A₂, ..., A_m are called the error-limiting sets, if

  i=1, 2, ..., m; j=1, 2, ..., n,  (24)

  where  is the complement set of A_j, Q( |x_i) is the feature function or the membership

 grade of x_i in . Let us call

  ,   (25)

  the rate-of-limiting-errors. In the equation, P(Y) is given, A_J represents {A₁, A₂, ..., A_n}, and P_AJ is the set of all possible channels  that make Equation (24) tenable.

 The function R(A_J) is different from function R(D) since it gives a limit for each y_j.  For example, in transmitting  data 1, 2, ...ÎA, the limit is A_j={i||i-j|1} for j=1, 2, ..., which means that once the  deviation is greater than 1, the entire transmission is failing.

 Theorem 4.3.2 Let the distortion d_ij =0 for x_iÎA_j   and d_ij =¥ for x_iÏA_j , for each i, j; P(Y) be a source and P(X|Y) be a channel. There is

  =H(Y). (26)

 Proof  Let us first prove R(A_J)=H(X) with the Lagrangian multiplier method. After analyses we know Shannon’s mutual information I_S(X;Y) does have the minimum value. We need to seek the minimum of I_S(X;Y) under limiting conditions given by Equation (24) and

  P(x_i|y_j)=1.   (27)

 Let

  ,   (28)    

  (where s_ij and m_j are  constants as Largrangian multipliers) and its partial derivative with respect to P(x_i|y_j) for each i, j be zero. Then there is

  ,  i=1, 2, ..., m;  j=1, 2, ..., n,   (29)

where l_j is a normalizing parameter. Since for each x_iÎA_j , ; thus

,  i=1, 2, ..., m;  j=1, 2, ..., n.    (30)

From Equations (25), (29), and (30), We can conclude that when

P(x_i|y_j)=P(x_i)Q(A_j|x_i)/Q(A_j)=Q(x_i|A_j), i=1, 2, ..., m; j=1, 2, ..., n    (31)

I_S(X;Y) reaches its minimum. From Equation (31) and Shannon's mutual information formula,

we have

.    (32)

Now let us prove R(D=0)=H(Y). From the classical rate-distortion theory, we know that when

R(D)=sD+ , ,   (33)

where s is a multiplier less than 0. Since when D=0, d_ij=0 for x_iÎA_j and d_ij= ¥ for x_i ÏA_j. Thus

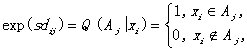 i=1, 2, ..., n; j=1,2,..., m.    (34)

and 1/l_j=Q(A_j) for each j so that

R(D=0)= = . Q.E.D.

If some of sets in A_J are fuzzy, i. e. Q(A_j|x_i)Î[0,1], and the limiting sets are determined by inequality

  , for all P(x_i|y_j)¹0, i=1,2,...,n; j=1,2,...,m. 

Then we can conclude

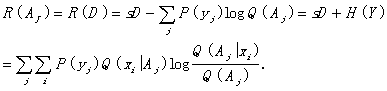 (35)

This is  Shannon’s mutual information as the special case of the generalized mutual information when the prediction is always vaguely true.