Abstract: A symmetrical model of color visions--the decoding model--has been established for us to understand color vision better. It adopts a new continuous value logic or fuzzy logic and works in a way very similar to the way a 3-8 decoder in a numerical circuit does. Unlike a popular zone model of color vision, the decoding model has four pairs of opponent colors: blue-yellow, green-magenta, red-cyan and white-black instead of three pairs: red-green, blue-yellow and white-black. By the decoding model, the evolution of color vision, color blindness and the perception of color appearance can be explained more concisely; Young and Helmholtz's tri-pigment theory and Hering's opponent theory can be unified more naturally.

Key words: color vision, color blindness, evolution of color vision, opponent process, fuzzy logic, symmetry.

1. Introduction

Young and Helmholtz's tri-pigment theory and Hering's opponent theory on color vision have been competing for a long time. A compromising point of view widely accepted is that color signals exist in tripigments at the zone of visual cones and in opponent signals at the zone of visual nerves. The mathematical model with this point of view is the zone model (Judd, 1949). There are many improved versions of it (Hurvich etc., 1957; Walraven, 1961; Hunt, 1982 and 1987; Nayatani etc., 1986; Seim etc., 1986). Yet, why are color signals processed in this way and how has color vision been evolving  The answers are still unclear. To answer these questions better, we built a model of color vision named the decoding model (Lu, 1986 and 1989).

The decoding model can also be said to be a new version of the zone model, but it is quite different from others. Compared with a popular zone model, the decoding model adopts fuzzy logical operations but not arithmetical operations; it is strictly symmetrical and produces three pairs of chromatic signals: blue-yellow, green- magenta and red-cyan instead of the two pairs: blue-yellow and red-green used in a popular zone model.

Please note that "red" and "green" in the Hering theory as well as in the popular zone model are different from "red" and "green" in the Young-(B,G,R)= m1 e1 + m2 e2 + m3 e3 (3)Helmholtz theory. In terms of the Young-Helmholtz theory or of the industry of color television, "red-green" in oppnent theory means a color between red and magenta, and "green"" is a color between green and cyan. The different of names of the colors are not important; the important issue is whether three pairs of unique colors possibly exist.

Some people perhaps think that psychological experimentation has shown that there are only four-unique colors and therefore a model producing six unique colors is unreasonable. However, we have several reasons for our opinion. First, it is not the final conclusion that only four unique colors exist; some people still insist that there should be more unique colors than four (Hardin, 1985). Second, more than two kinds of chromatic opponent signals in monkey retina was found by physiological experiments (de Monasterio, etc., 1975). Third, a model possessing symmetry seems better in theory; a symmetrical model of color vision needs six unique colors. Fourth, color vision is evolving; we can image that the number of unique colors is increasing from four to six. Even if there are some similarities between red and magenta or blue and cyan, it is only because some units in retina work still on lower levels at the same time. The fifth reason will be discussed later.

The decoding model has been verified by predicting color appearance (Lu, 1989). The uniformity of the -r_c-z (for angle as hue since editorial reason), system based on this model is similar to CIE LAB. In this paper, we are concerned with the mathematical aspect of the model and the explanation of various phenomena of color vision.

Now we discuss the mathematical aspect of the model without regard to how three receptor outputs, B, G and R, are transformed from the data, CIE X, Y, Z,of color optics.

The binary 3-8 decoder is frequently used in computers or numerical circuits for selecting one memory from eight. If B, G and R are binary switching variables, i.e. B, G and R take values in the set {0,1}, as three inputs to a 3-8 decoder, then eight outputs will be [B G R], ], [B G R], [B G R], [B G R], [B G R], [B G R]and [B G R] ( [...] Denotes a logical expression, and B equals B with a line on on top for editorial reason ). For example, if B=G=0 and R=1, then [B G R]=1 and others equal 0.

Let B, G and R represent the outputs of three cones and a color be denoted by a vector (B, G, R). Hence [B G R], [B G R ],…, [B G R ] stand for the magnitude of eight color signals: blackness, redness, ..., whiteness (see Table I).

Table 1: Relation between B, G and R and values of eight output codes or color Signals: black, red, yell, green, cyan, blue, magenta, white

Now, suppose that B, G and R vary from the binary switching variables into the fuzzy switching variables, i.e. B, G and R take continuous values in the set [0, 1 ]. With the special fuzzy logic (Lu, 1991), which was created for the model, we can extend the binary 3-8 decoding into the fuzzy 3-8 decoding (Lu, 1986).The values of output codes are illustrated by Figure 1.

when B>G>R, the values of four output codes are shown and other values are equal to zero. Let max(a,b) stand for the maximum of a and b, min(a,b) for the minimum of a and b, and so on. Hence

(1 )

The others can be calculated in the same way.

The problem now is how to reach , r_c , s, and rs, which are supposed to represent hue, colorfulness, brightness, and saturation, from B, G and R.

For any given color denoted by (B, G, R), there is a equation :

            (B,G,R) = [B G R ](0,0,1)+[B G R ](0,1,1)+ [B G R ](0,1,0)

                            +[B G R ](1,1,0) + [B G R ](1,0,0)+ [B G R ](1,0,1)+ [B G R](1,1,1)

(2)

which means that any color can be broken down into the combination of white and six unique colors in different ratios. In the equation, (0, 0, 1) stands for the most saturated red, i.e. unique red, and the coefficient [B G R ]is the degree of redness of the color (B, G, R), and so on. It is coincident that only three items on the right of equation (2) may not be zero for a given color and the three cardinal vectors or unique colors must be at the three vertexes of one of six sectors in Figure 2. Hence equation (2) can be changed into

(B,G,R)= m1 e1 + m2 e2 + m3 e3

(3)

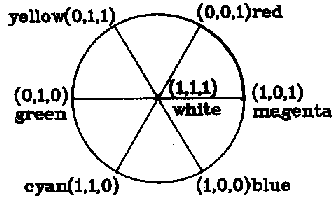
Figure 2. Breaking down of a color (B, G, R) 

For a given color, cardinal vectors in the three non zero items must be at the three vertexes of a sector.

where e1, e2, e3 are three cardinal vectors in three non zero items and e3 = (1, 1, 1); m1, m2 are coefficients or magnitudes of output codes related to e1, e2 respectively; m3 =[BGR ] is for whiteness.

Suppose the angles at which e1 and e2 are locate (see Figure 2) are 1 and 2. Let

 = (m11 +m22) /(m1 + m2 + m3)

rc = m1 + m2

z = m1 + m2 + m3 ( or z =max(B,G,R))

rs = rc / z

(4)

The , rc, z, rs will represent hue, colorfulness, brightness, and saturation of (B, G, R) if B, G and R are obtained by appropriate linear and nonlinear transformations of spectral tristimulus X, Y, Z (Lu,1989). According to the decoding model, relation between brightness, colorfulness, whiteness, blackness and B, G and R is shown in Figure 3 where med(B, G, R) is the medium one or second one of B, G and R. For example, med(1,3,5)=3, med(1,2,5)=2, med(1,5,5)=5, med(1,1,5)=1.

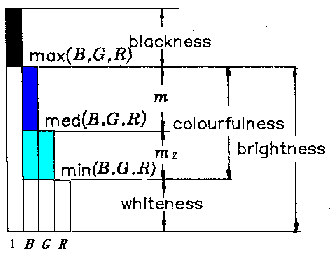
Figure 3: Relation between B, G and R and brightness, colorfulness, whiteness, and blackness according to the decoding model

We use Venn's Diagram to show the essence of the process. Let ^, V, - denote the three set operations: union, intersection,and complement respectively; B, G and R represent the three circular fields respectively (see Figure 4). For convenience, we also use "_" for complement operation and omit ^. The eighth fields can be represented by [B G R ], [B G R],…, and [B G R ].

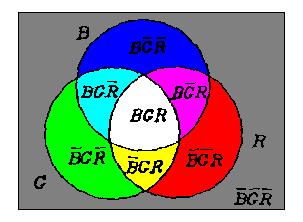
Figure 4. Venn's diagram to show the essence of the opponent process

From B, G and R, we can first get

M = BG VBR VGR

(5)

which represents the intersecting fields of two or three of B,G and R, and then we have

(6)

If the round fields B, G and R are illuminated by blue, green, and red lights, three pairs of opponent colors will be displayed on the six fields; for example, blue and yellow will be displayed on the fields B M = B G R and B M = B G R.

Now let B, G and R denote three receptor outputs and take values in the set [0, 1 ] again, and the set operations be substituted by the fuzzy logic operations: ^, V, _ ( stands for maximum, for minimum and can be omitted). First we obtain med(B, G, R):

M =med(B, G, R) =[ BG V BR V GR ]

or M =max(min(B, G), min(B, R), min(G, R))

( 7)

and then we get three opponent signals, blueness-yellowness (Mby by B-M), greenness-magentaness (Mgm by G-M), and redness-cyanness (Mrc by R-M). The calculation as following is surprisingly simple.

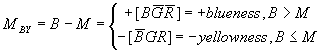
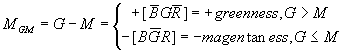
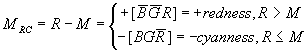
( 8)

The above results make use of DeMorgon's law. The logical proof for redness is:

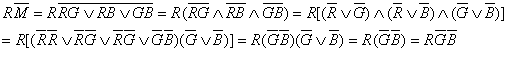
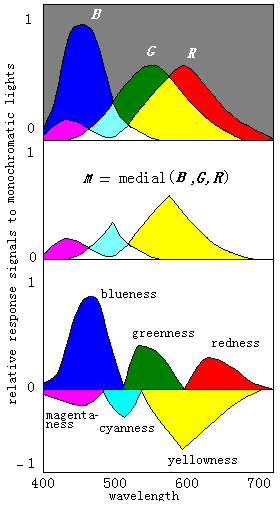
Figure 5: Opponent process corresponding to different monochromatic lights.

First M, the medium of B, G and R, is obtained; and then three pairs of chromatic opponent signals are calculated by subtracting M from B, G and R

The opponent process corresponding to different monochromatic lights is shown in Figure 5 where for convenience the three response curves are assumed. We can also consider the upper part of Figure 5 as a Venn's diagram. There are eight divided fields.

The length of the part of a vertical line in a field is just the magnitude of the corresponding unique color signal. These fields can illustrate the change of color vision caused by different monochromatic lights well.

The diagram of the principle for the opponent processing in the decoding model is shown in Figure 6. In order to demonstrate the process of color signals both in the retina and in the cortex, we have built a completely physical model of color vision (see

Figure 7 that works as well as we had expected).

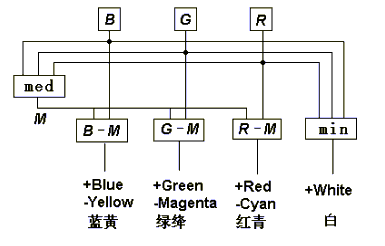
Figure 6  Symmetrical opponent process in the decoding model

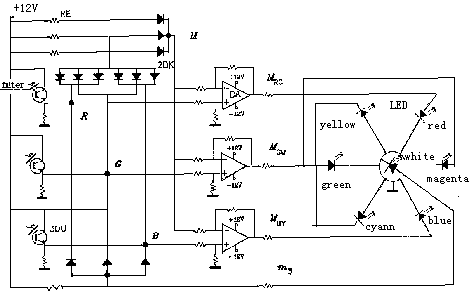
Figure 7: Diagram of principle of the physical model of color vision

Here 3DU is a phototransistor and imitates a cone; DA is a differential amplifier imitating the bipolar; LED is a light emittingdiode supposed to be color cells in cortex; RE is a resister and 2DK is a diode. The array of diodes and resisters on the upperleft is supposed to be a horizontal cell and gives

output med(B,G,R).

The physical model suggests that, in the cortex, there be seven color cells, which receive white and six unique color signals; the brain produces brightness and colorfulness by simple addition, and turns out hue and saturation by the method of weighing. Perhaps there are also some processes of color signals on lower levels; for example, some white cells probably receive faster conducting signals directly from cones and rods (Kaplan, 1982). The decoding model does not cover this subject. Thus, it does not provide a measure as luminance Y in CIE XYZ or light value V in the Munsell system, but z for brightness.

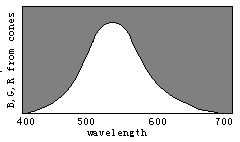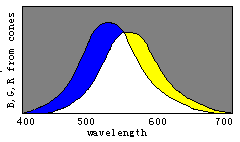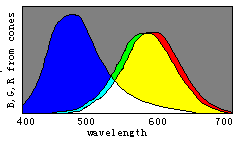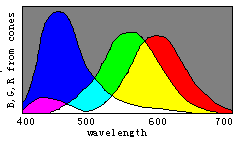
Figure 8. Evolution of color vision illustrated by the separations of sensitivity curves

Man with one kind of cones could perceive only two totally different colors: white and black; With W() splitting into B() and Y(), man could gradually discern four totally different colors, blue, yellow, white, and black. With Y() splitting into G() and R(), man could gradually more totally different colors.

According to the decoding model, we can easily explain the evolution of color vision by the changes of three sensitivity curves of cones (see Figure 8). Please imagine that curves R() and G() gradually approach one another to become one curve named Y() ; we would see the fields representing red, green, cyan, and magenta disappear gradually. Further, let curves B() and Y() approach one another gradually to become one curve named W() ; we would seen the fields representing blue and yellow

disappear gradually and only the black and white fields remain. Therefore, we can imagine that color vision was evolving in an opposite procedure. First, there was only one kind of cones in the human retina and only two totally different colors -- black and white -- could be discerned. Then, with color vision evolving, the cones split into two kinds that had different spectral sensitivities so that blue and yellow were also perceived. After that, the cones split into three kinds so that more colors were perceived.

We may draw the conclusion that n different kinds of cones can cause 2ⁿ totally different color perceptions for n=1 , 2, 3. As n=4 , the conclusion seems also true. We have built a symmetrical model of four primary colors for robots (Lu, 1987) that has 14 "unique colors", which can be symmetrically put on the surface of a ball, besides "white" (1, 1, 1, 1) and "black" (0, 0, 0, 0). We can get a "color" ball that has many properties very similar to those in the Newton color plate.

Perhaps the evolution might have been in a somewhat different way. For example, the curve W() first split into R() and C() related to cyan, then C() split into B()and G().

Color blindness has been discussed by many researchers (Hsia at el., 1965). It can also be easily explained by the sensitivity curves of cones being too close to each other. For example, monochromatism can be explained by the theory that the sensitivity curves B(), G() and R()have not yet separated; Red green blindness can be explained by the theory that the curves G() and R() have not yet separated. From this point of view, some red green blindness can be identified as protanopia or deuteranopia only because the peak of Y()may have shorter or longer wavelength. Tritanopia and tetartanopia can be illustrated by the theory that the B() and G() , or B() and R() , have not yet separated so that each kind of color blindness can only perceive two chromatic colors: red and cyan or green and magenta. All kinds of color blindness above can be imitated by the physical model with two of three of the 3DUs always obtain the same inputs.

It is obvious that the color anomalous can be explained in a similar way. By the decoding model, we can also explain the color blindness by the mixture of two or three of outputs of three 3DUs (omitted).

4 Verification

    Assume that three stimulus B', G', R' of cones are linear transformation of X, Y, Z of CIE; and the three output color signals of cones  B, G, R are nolinear transformation of B', G' R'. Using above model, we can obtain a unique color system   -rc-z. Some result are shown bellow.

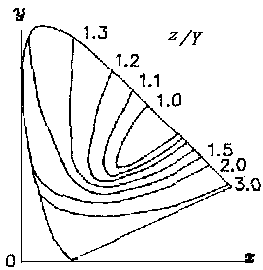
Figure 8  z-equal lines on x-y chromacity chart (under the same luminosity Y) 

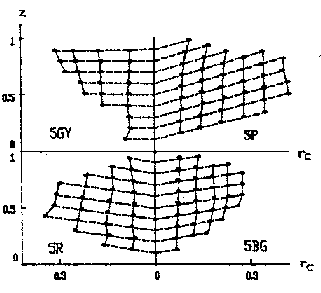
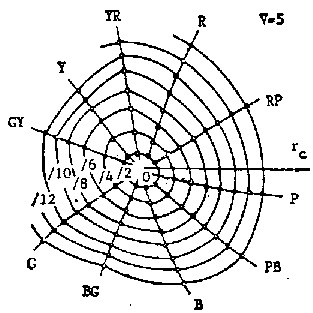
Figure 9 A Uniform color system based on the decoding model

To understand color vision better, we will discuss some questions now. Suppose there are only three kinds of different color cells in the cortex. Every kind receives one kind of signals that directly come from one kind of cones in the simplest way. Why does the mechanism of color vision give us more than three totally different color perceptions  Our answer is that, in order to make the brain more easily distinguish different objects, the mechanism pretreats color signals to get hue that reflects specialties of spectra of objects better. It is not hard to understand that the more unique colors or hue that are perceived, the more information the color vision can provide.

The explanation of information is the fifth reason for our opinion on the number of unique colors.

Fortunately, our consideration of information about colors has also resulted in an improved information theory (Lu, 1991) that can provide relation between the information of colors and men's color is crimination well.

There is another question. Why do color signals exist in tri-pigments at the zone of visual cones, and in opponent colors at the zone of visual nerves; or why does the retina process color signals in this way  Our answer is that this is due to the fact that this is the simplest method. From the physical model,

we can find that, in this way, the six unique color signals can be most simply produced and conducted.

In comparison with a popular zone model in which there are only two pairs of chromatic opponent colors, the decoding model also has the following advantages in addition to those in answering the above two questions.

(1) The decoding model is more concise and symmetrical and uses no modification parameters.

(2) It can explain the evolution of color vision and color blindness more easily.

(3) In the decoding model, theoretically, a unique color signal can be uniquely obtained; for example, while (B,G,R)=(0, 0, 1),only redness is not zero, whiteness and others are zero. Yet, in a popular zone model, an chromatic signal can not be uniquely produced because whiteness can not be zero except for (B,G,R)=(0, 0, 0) . From the point of view of the information theory, this is not good.

(4) The decoding model is more compatible with the laws of the color mixture that is used on the screen of a color television.

(5) We can use the decoding model to explain the phenomenon of negative after image more conveniently; for example, when the sensitivity of the R cone falls down, [R B G]   for cyanness will increase over zero for a neutral color so that a neutral color looks cyan.

Compared with some models like the Hunt model (Hunt, 1987), the decoding model also has some is advantages. For example, it only describes the major processing mode of color signals without the regard to rods, adaptation and the measure like Y in CIE XYZ or V in Munsell's system.

The decoding model can also be tested by neuron-physiology. According to the decoding model, we can make two predictions. One is that there should be some fuzzy logic gates, which execute the operations of maximum, minimum, and even medium, in the human retina. Another is that some chromatic opponent units should exist in visual nerves. The response curve of such a unit has a horizontal line, instead of a neutral point, between its positive and negative parts (see figure 5). These logic gates and opponent units have not been mentioned yet, because either most experiments were made with animals whose color vision is less complete then the man's, or the direction of an appropriate theory was absent. For example, a widely used method to identify a chromatic opponent unit is to find its neutral point (Volois,1966); however, this method is not suitable to identifying the opponent unit suggested above. We believe that the predicted logic gates and the opponent units will be found soon by physiologists who pay attention to them.

1 . De Monasterio, F. M.: Gouras P. and Tollhurst D J., Trichromatic color opponency in ganglion cells of therhesus monkey    retina, J. Physiol. 252 (1975), 197-216

2 De Volois, R. L.: Abramov I and Jacobs G H. Analysis of response properties of LGN cells J. Opt. Soc. Am. 56 (1966),966-977

3 Hardin, C. L.: The resemblances of colors, Philosophical Studies 48 (1985), 35-47

4 Hsia, Y. and Grapham, C. H.: Color blindness, in Visual Perception , C. H. Grapham ed., Wiley, New York, 1965, Chap. 14, Tab.14.2

5 Hunt, R. W. G.: A model of color vision for predicting color appearance, Color Res. Appl. 7 (1982), 95-112

6 Hunt, R. W. G.: A model of color vision for predicting color appearance in various viewing conditions, Color Res. Appl. 12 (1987), 293-314

7 Hurvich, L. M.: and Jameson D. An opponent-process theory of color vision, Psychological Review 64 (1957), 384-404

8 Judd, D. B.: Response functions for types of vision according to the Muller theory, J. Res. Natl. Bur. Std. 42 ,1(1949)

9 Kaplan, E. and Shapley, R. M.: X and Y cells in the lateral geniculale nucleus of Macaque monkeys, J. Physiol. 330 (1982),125-143

10 Lu, C.G.: (1986) New Theory of color vision and simulation of mechanism, Developments in Psychology   in China), 14, 36 45.

11 Lu, C.G.: (1987) Models of color vision for robots. Robot ( A Journal of Chinese Society of Automation) ,1, No.6,39 46(1987).

12 Lu, C. G.: (1989) Decoding model and its verification, ACTA OPTICA SINICA, 9, 158 163.

13 Lu, C.G.: (1990) Shannon equations reform and applications, BUSEFAL, 44, 45 52.

14 Nayatani, Y. and Takahama, K. and Sobagaki, H.: Prediction of color appearance under various adapting conditions, Color Res. Appl. 11 (1986), 62-71

15 Seim, T. and Valberg, A.: Towards an uniform color space: A better formula to describe the Munsell and OSA color scales, Color Res. Appl. 11 (1986), 11-24

16 Sperling, H. G.: and Harwerth R S. Red-green cone interactions in the increment-threshold spectral sensitivity of primates, Science 172 (1987), 180-184

17 Walraven, P. L.: On the Bezold-Brucke phenomenon, J. Opt. Soc. Am. 51 (1961), 1113-1116