
New Method of Solid Boolean Operations with Continuous Value Logic
So short program, one never imagines!
Welcome Co-operating and Buying this Technique
””
New method uses continuous value logic to replace complicated if-then judgments. It makes program possess simplicity, reliability, and generality. In the three Boolean operations intersection,combination, and subtraction . +, - , operations,is most simple. If A-B can been resolved, then A+B=A-B+AB can also been resolved. So, Critical problem is how to obtain A-B. Follows are several samples of A-B. The most important thing is that we needn't worry about relative positions between A and B. The main program for A-B is shorter than 20 lines long no matter what boundary functions A and B have . For the bridge drawing,all source program including the definitions of boundaries of functions of A and B is shorter than 60 lines long. The method of plenary Boolean operations can been used to extract machining regions from the constructive-solid-geometry representation of a given object.
A-B Drawing 1 A: A cube minus a loop£» B: a solid with upper boundary produced by sin(x) and lower boundary by a loop.

Download program for drawing the above bridge
A-B Drawing 2 A: a cub2+column£¬ B: a loop
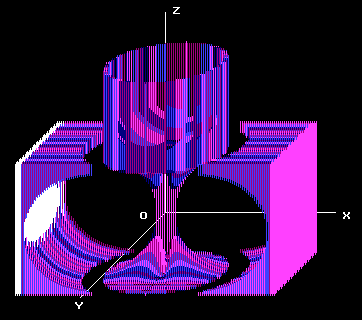
A-B Drawing 3 a cube minus a ball

Drawing 4 a ball minus a cube

Plenary A-B: A with boundaries x1,x2, y1, y2; B with boundaries x3, x4, y3, y4
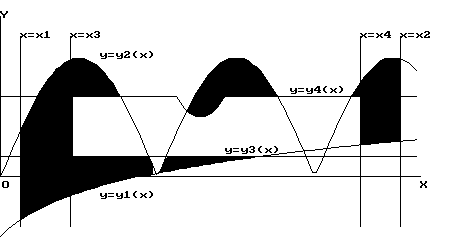
The method of plenary Boolean operations can been used to extract machining regions from the constructive-solid-geometry representation of a given object.
””