借助罩鱼模型从Hartley信息公式推导出广义信息公式
鲁晨光 (独立研究者)
摘要:为了把经典信息论推广到日常信息交流(包括语言通信和感觉通信),本文通过罩鱼模型,直观地说明,如何从简单的Hartley信息量公式,一步一步推广,得到广义信息量公式。这一广义信息公式正好是连接Shannon信息论Popper知识进化论的桥梁。
关键词:Hartley信息, Shannon信息,Kullback公式,测量信息,感觉信息,语义信息,Popper理论
Deducing General
Information Formula from Hartley’s Information Formula
with the Help of
Fish-covering Model
Lu Chenguang
(independent researcher)
Survival99@hotmail.com
Abstract: To
extend the classical information theory to daily information exchange including
linguistic communication and sensory communication, this paper intuitively
explains, with the fish-covering model, how to extend simple Hartley’s formula
of information amount to the formula of general information amount step by
step. The later formula happens to be a bridge between
Keywords: Hartley
information, Shannon information,Kullback
formula, measuring information,
sensory information, semantic
information, Popper’s theory.
1.
序言
笔者在《广义信息论》【1】中提出的广义信息(量)公式是Hartley和Shannon的经典信息(量)公式的自然推广。为了使大家更好地理解广义信息公式的合理性,本文借助罩鱼模型,从Hartley信息公式逐步推导出广义信息公式。
2 Hartley信息公式和图解通信的罩鱼模型
Hartley信息公式【2】是
I=logN
(1)
其中I表示确定N个等概率事件中的一个出现时提供的信息。如果事件y把不确定范围从N1个缩小为N2个,那么信息就等于
Ir=I1-I2=logN1-logN2=log(N1/N2)
(2)
我们且称这个公式是Hartely相对信息公式。在说明这个公式性质之前,我讲一个用鱼罩子捕鱼的故事。
鱼罩子是用篾做的,象过去家家户户用的烤火罩,形如半球壳,上面有个圆口,便于抓鱼。它适合浅水捕鱼。我小时候看人家用鱼罩子捕鱼,我也拿个通了底的篮子学着捕。也真捕到了。后来我总结经验:鱼罩子大,容易罩住鱼,但是罩住以后抓鱼困难些。如果鱼罩子和池塘一样大,那就百发百中,但是没有意义,因为要抓到鱼,还是一样很难。我用篮子或小鱼罩子罩鱼,虽然罩中困难,但是罩到了,抓就很容易。
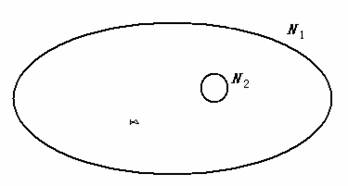
图1 度量信息的罩鱼模型
一个不确定事件就像是池塘里随机出现的一条鱼。设语句y=“罩住鱼了”,y就提供关于鱼的位置信息。如N1是池塘的面积,N2是鱼罩子底面积, 那么信息就是I=log( N1/ N2)。N2相对N1越小,信息量越大,这正反映了篮子的优点。当N2= N1时,信息是0, 这正反映:鱼罩子和池塘一样大,罩中也没有意义。至于鱼罩子和篮子相比的优点(不容易出错),上面公式不能反映,因为使用Hartley公式有这样的前提:客观事件必然是N2个事件中的一个。相当于假设:鱼罩子或篮子不会罩不中鱼。后面推导出的广义信息公式将包容“罩不中”情况。
3 模型改进――事件空间变为可能性空间
用Hartley公式计算信息,要求N个事件是等概率的, 即P=1/N,但是通常的情况并不如此。 比如,鱼在水深的地方可能性大些,在水浅的地方可能性小些。这时候如何处理? 这时候我们用实际的概率代替假设的相等的概率,即用P1代替1/ N1, 用P2代替1/ N2。于是,Hartley信息公式就变为
I=log(1/P)
(3)
上面的相对信息公式就变为:
Ir =log(P2/
P1)
(4)
4.以集合为条件的相对信息公式
我们设鱼所在位置为随机变量X, 它取值于集合A中元素,
A={x1, x2,
…}; 随机事件Y是关于X所在区域(即鱼罩子覆盖区域)的报告,Y取值于B中元素,B={y1, y2,…},
yj=“xi ∈Aj”(“xi在集合Aj中”)。于时, P1可写成P(xi), P2可写成P(xi|xi ∈Aj)。 我们简记P(xi|Aj)= P(xi|xi ∈Aj),P(xi|Aj)是以集合为条件的条件概率。于是上面相对信息公式变为
![]()
(5)
这个公式为是以集合为条件的相对信息公式。因为它基于罩鱼模型,我们称之为“罩鱼信息公式”。值得注意的是,一般情况下,以集合为条件的条件概率P(xi|Aj)和以语句yj为条件的条件概率P(xi |yj)是不等的。
P(xi|yj)= P(xi|“xi ∈Aj”)=P(xi |“xi ∈Aj” 被报告)
(6)
报告yj可能不准,也可能是谎言,然而xi ∈Aj表示yj为真。即
P(xi|Aj)= P(xi|xi ∈Aj)=P(xi |“xi ∈Aj” 为真)
(7)
如果两者相等,即报告(预言或命题)总是真的,或总是和事实一致,那么上面公式就变为经典信息量公式【2】:
![]()
(8)
对它求平均就得到Shannon互信息公式。
5.集合信息公式的性质及其用于测量信息的度量
现在我们以温度测量为例,说明如何用罩鱼信息公式度量测量信息。
一个温度读数可看成是一个关于鱼罩子覆盖区域的报告,实际温度可看成鱼的位置。于是罩鱼模型可以用于温度测量。假设温度集合A={x1,
x2, …},温度读数集合B={y1,
y2,…}, X和Y是表示温度和温度读数的随机变量,并且读数是Y= yj
时,最大可能的温度是xj 。假设“鱼罩子”清晰,即当读数是yj 时, 实际的温度应在某个确定范围Aj内,
比如Aj =[xj-0.2,
xj+0.2]。于是,实际xi发生时,yj提供的信息如上面的罩鱼信息公式(5)所示。
这里我们并不保证读数yj一定正确,如果操作不当,读数不准,计算出的信息就是负的(集合清晰时信息是负无穷大)。
设集合Aj的特征函数是Q(Aj|xi)(取值0或1,呈矩形),
根据Bayes公式, 有
P(xi
|Aj)=Q(Aj | xi )P(xi )/Q(Aj
)
(9)
其中Q(Aj)是Q(Aj
| xi )的平均值。即
![]()
(10)
由(9)和(10),我们得到罩鱼信息公式的另一种形式:
![]()
(11)
它是经典信息公式和广义信息公式之间的过渡。上面各变量及信息量随xi的变化如图2所示。
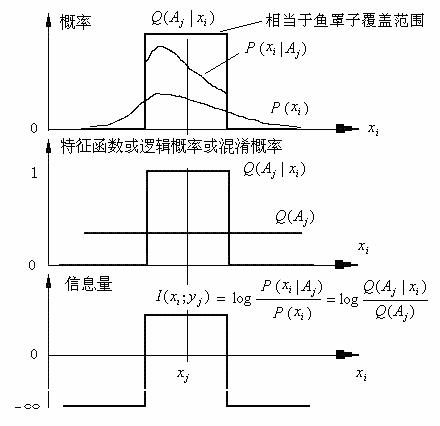
图2 罩鱼信息公式图解
6.混淆范围模糊时的测量信息和降水量预测信息――广义信息
温度测量读数提供的信息和降水量数值预测(比如:“降水量大约是
I=m-k|xi-10|
(12)
就比较符合常识(参看图3)。
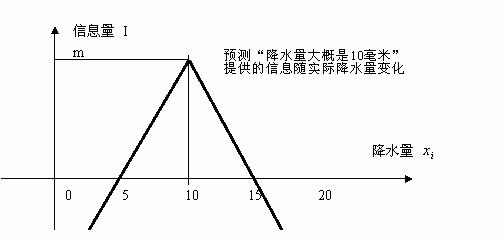
图3 一个假想的较为符合常识的信息量公式图解
但是公式(12)不能计算这样的预测――“降水量不小于
下面我们推导出一个不但具有式(12)优点,也能弥补其缺点的信息公式。
上面我们假定,Aj是清晰集合。特征函数Q(Aj|xi)可理解为xi和xj相混淆的概率。对于清晰集合Aj,如果xi在Aj中,混淆概率是1, 否则是0。而实际情况是,Aj可能是模糊的,混淆概率可能在0和1之间变化。
混淆概率实际上是模糊集合隶属度以及命题逻辑概率的不同说法,函数曲线Q(Aj|xi)可以来自清晰集合统计【4】(参看图4)。
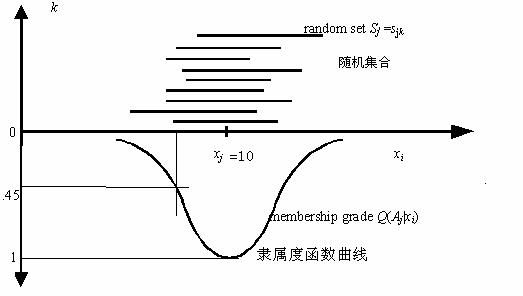
图4 混淆概率(或隶属度或逻辑概率)函数曲线来自清晰集合特征函数的统计
具体做法是:假设我们做许多次试验:当读数Y= yj时,改变xi, 只有当xi和xj差异大到一定程度,读数yj才会变化。 不引起读数变化的所有xi构成的集合是一个清晰集合,许多次(设为n->无穷大)试验得到许多这样的集合sj1, sj2,…sjn,然后我们定义
![]()
(13)
是xi和xj 相混淆的混淆概率, 它也就是xi在模糊集合Aj 上的隶属度,或命题yj=“ xi在模糊集合Aj中”的逻辑概率。其中Q(sjk|xi)是集合sjk的特征函数 (等于0或1)。
要计算混淆范围模糊时的温度测量信息, 我们只需要用混淆概率函数取代前面的集合特征函数,公式形式如同(11),是:
![]()
(14)
这就是广义信息(量)公式。不同的是,这里Q(Aj|xi)是山形函数而不是矩形函数。广义信息公式可以理解为鱼罩子边界模糊时的罩鱼信息公式。
公式(14)的几何性质如图5所示。它表明,当读数是yj时,
实际发生的xi 与xj差别越大,信息量越小。差别大到一定程度,信息量就是负的;Q(Aj)越小,信息的绝对值越大。
用这个公式度量数字图像信息、 海啸预测信息、设计图纸信息等也是可行的[1]。
7.感觉信息度量
我们且考虑人眼相应不同灰度等级的象素的视觉信息。假设灰度是X=xi, 相应的感觉是Y=yj ,
所有和xj相混淆的xi构成模糊集合Aj, Q(Aj|xi)是人眼把xi和xj相混淆的概率。 于是,视觉信息和温度测量信息在本质上完全相同,用公式(14)就可以度量一种灰度视觉yj提供的关于xi信息。据此,笔者根据感官分辨力优化图像通信得到许多有意义结论,参看文献【5】。
8.语义信息度量
在笔者看来,预测信息是比事实陈述信息更具有一般性的语义信息。当预测和事实一致时, 预测信息就变为事实陈述信息。所以,度量一般语义信息必须考虑预测和事实是否一致。
如果把Q(Aj|xi)(在0和1之间变化)理解为命题yj的可信度或逻辑概率,公式(14)就可以用于度量语义信息或预测信息(参看图5)。这时,我们可以假设相应每个命题yj存在一个柏拉图式的理念xj(可能不在Aj中), 命题yj(xj)的可信度是1。这样,我们就可以把Q(Aj|xi)理解为xi和理念xj相混淆的混淆概率。于是语义信息和测量信息在本质上相同。
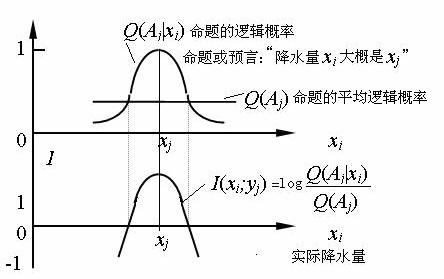
图5
广义信息(测量信息,感觉信息,预测信息)公式图解
不难证明,该公式对于“明天有小到中雨”这样的非数值预测的信息度量也是合理的;在预测不准时算出的信息量(可能是负的)也是合理的【1】。负信息表示错误的预测或谎言会减少我们已有的信息。
上面的Q(Aj)也可以说是谓词yj(X)的逻辑概率, 或命题yj的先验逻辑概率或平均逻辑概率。于是,语义信息量公式可以写成下面易于理解的形式

(15)
9.广义Kullback公式,广义互信息公式及广义通信优化
我们对广义信息I(xi; yj)求平均, 就得到广义Kullback公式
![]()
(16)
其中对数后面的P(xi)也可以不是来自统计,而是来自主观估计,这时候我们记它为Q(xi),这时P(X|Aj)变为Q(X|Aj)。广义Kullback信息公式的性质可以通过图6说明。

图6 广义Kullback公式性质图解
可以证明,预测Q(X|Aj)和事实P(X|yj)越是重合,信息量越大, 信源P(X)或先验估计Q(X)越是与事实P(X|yj)不同(表示预测的事情越是出乎意外),信息量越大。这和Popper的科学进步评价准则是一致的(后面讲到)。当Q(X|Aj)=P(X|yj)时,上面公式就变为Kullback公式。再对I(X; yj)求平均,我们得到广义互信息公式
I(X;Y)=H(X)-H( X|Y)=H( Y)-H( Y|X)
(17)
其中
![]()
(18)
![]()
(19)
![]()
(20)
![]()
(21)
其中,H(X)被称之为预测熵,它反映主观预测的信源和实际信源不一致时,按最优方式编码的平均码长下限。H(X|Y)是以一组集合Aj, j=1,2,… 为条件的的条件熵。H(Y)是广义熵,当集合清晰时,它反映给定误差限制集合时的最短平均码长【1】, 正巧就是复杂性理论中的复杂性失真率(rate -complexity-distortion)【6】。H(Y|X)是广义条件熵或模糊熵。可以证明Deluca-Termini模糊熵【7】是上面模糊熵的特例。容易证明,模糊性会减少信息的绝对值,但是在预测不准的情况下,模糊性可以减小负信息。这和鱼罩子大则罩中容易同理。这也就是为什么预言家大多喜欢使用模糊语言,为什么对于可能不准确的预测,我们往往做模糊理解。对于感觉信息,感官分辨率低则模糊熵大,信息量小。另一方面,降低感观分辨率会减小噪声带来的信息损失;这就是为什么电视图像雪花点过多时,离得远些,视觉效果反而好些。
广义互信息公式对优化广义通信有着重要意义。经典信息率失真理论研究的是通信优化问题:给定失真限制,Shannon信息(传输的比特)最少需要多少?或者是,在给定Shannon信息时,失真范围最小可达多少。可惜那里失真是人为定义的,没有客观标准。现在有了广义信息公式,我们就可以用广义信息量替代失真量作为评价通信质量的准则,把信息率失真论改进为保精度信息率论,由此可以得到许多重要结论【1】,比如:听信算命先生信口开会减少我们已有的信息;要用谎言迷惑敌人,也需要一定的客观信息;人眼感官分辨率和图像精度之间存在最优匹配,视觉分辨率有限,图像精度太高反而不好。
如果先验估计Q(X)等于信原P(X), 预测熵H(X)就变为Shannon熵。进一步,如果事实P(X|yj)等于预测Q(X|Aj),那么就有P(yj)=Q(Aj)(对于所有j), 广义熵H(Y)也变为Shannon熵,广义互信息就变为Shannon互信息。可见,Shannon互信息是广义互信息在预测和事实总是一致时的特例。
10. 广义信息公式和Popper科学进化论的一致性
广义信息公式(14)的性质如图7所示。为了便于理解,我们不妨把图中预测理解为对股市指数、降水量、温度……或产量的预测。三个山型曲线表示三个不同预测――用以比较精确预测和模糊预测, 对更偶然事件的预测和对不很偶然事件的预测。图中结论:精确预测信息的绝对值更大,但因容易出错而更容易导致负信息;把更偶然事件预测准了信息量更大。
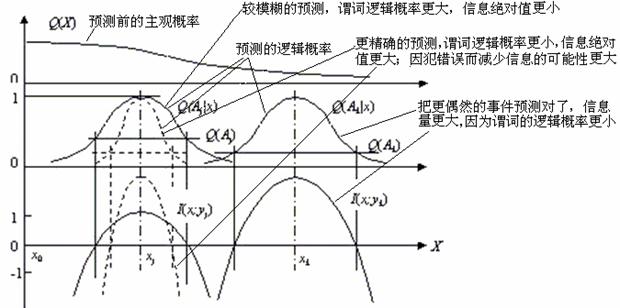
图7 广义信息公式的性质
关于科学理论的进步标准,Popper写道:
“凡是包含更大量的经验信息或内容的理论,也即在逻辑上更有力的理论,凡是具有更大的解释力和预测力的理论,从而可以通过把所预测的事实同观察加以比较而经得起更严格检验的理论,就更为可取。总之,我们宁取一种有趣、大胆、信息丰富的理论,而不取一种平庸的理论。”【8】
根据Popper的证伪理论,命题在逻辑上越容易被证伪(也就是说逻辑概率Q(Aj)越小),而事实上经得起检验(也就是说Q(Aj|xi)越大),命题提供的信息就越多,就越有意义。反之,在逻辑上不能被证伪的永真命题(也就是说Q(Aj|xi)=Q(Aj)=1)不含有信息,没有科学意义。
可见,虽然广义信息公式是经典信息公式的自然推广,但是它和Popper的科学进化论有惊人的一致性。
参考文献
[1]鲁晨光,广义信息论,中国科学技术大学出版社,1993
[2]
Hartley, R. V. L. Transmission of information,
[3]Shannon,
C. E. A mathematical theory of communication,Bell System Technical Journal,27 (1948),379—429,623—656
[4]汪培庄, 模糊集和随机集落影,北京师范大学出版社,1984.
[5] Lu,
Chenguang (鲁晨光) “A generalization of Shannon's
information theory" , Int. J. of General Systems, 28: (6) 1999,453-490
[6]Li, Ming and Vitanyi, Paul, An Introduction
to Kolmogorov Complexity and Its Applications,
[7] De Luca A. and Termini,S.: A definition of nonprobabilistic entropy in the
setting of fuzzy sets,Infor. Contr. 20(1972),201—312
[8]〔英〕波普尔,付季重等译, 猜想和反驳——科学知识的增长,上海译文出版社,1986