笔者的发现的译码模型
笔者早在
发现的过程大概是这样的。我这个人在理论上是一个理想主义者，这使得我很不满意流行的Walraven的阶段模型。记得当时我面对一个类似图6 那样的三刺激值曲线图， 开始我力图通过加减由B,G,R得出能反映颜色感觉的物理量――红、黄、绿…等颜色信号强度。当我这样做的时候，我希望由(B,G,R)=(0,0,1)得出红是1，绿、黄、蓝…都是0; 而不是象流行的Walraven模型那样，这时黄色信号Y=G+R等于1，白色信号W=B+G+R也等于1。 我希望由(B,G,R)=(0,1,1)得出黄是1，红、绿、蓝…都是0； 而不是而不是象Walraven段模型那样，这时G=1, R=1，W=2。我为此画了很多表明运算结果的草图。后来我终于发现算术运算是不可能有那样的结果的，于是我考虑到逻辑运算。由于我在南京航空学院读书时，毕业设计就是逻辑电路设计，所以我对逻辑问题很敏感。思路一旦转换，我很快就得出这样的结论：我们把三刺激值曲线下面的三个区域当作三个集合，三个集合作逻辑运算就得到8个互不相交的集合，这八个区域画上不同的颜色：红、黄、绿、青、蓝、绛、白、黑；那么波长为λ的竖线在不同区域上的相对长度就是不同色觉的相对强度(参看封面最下边的图)。
然而，要把二维平面上的逻辑运算转换成三刺激值B,G,R或函数b(λ), g(λ), r(λ)的逻辑运算，经典逻辑没有解决办法，其他逻辑多值逻辑，比如模糊逻辑也不行。为此笔者专门定义了“连续值逻辑准布尔代数”，通过这一代数，我们就可以把红、黄、绿、青、蓝、绛、白、黑8种色觉信号的大小表达为B,G,R的逻辑函数。比如：红色(0,0,1)信号的大小是--其含义是R既超出B也超出G的部分。即：
黄色信号的大小是
――其含义是G和R共有的且超出B的部分。即：
=
max(0, min(G, R)-B)
B,G,R的几种逻辑函数值如图9所示。其他可以类推。
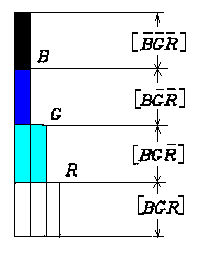
图
9 逻辑函数值图解
表
4 8个心理颜色信号的大小|
颜色名称 |
矢量 |
逻辑函数 |
假设 (B,G,R)=(0.1, 0.3, 0.8) |
|
黑 |
(0,0,0) |
|
0.2 |
|
红 |
(0,0,1) |
|
0.5 |
|
黄 |
(0,1,1) |
|
0.2 |
|
绿 |
(0,1,0) |
|
0 |
|
青 |
(1,1,0) |
|
0 |
|
蓝 |
(1,0,0) |
|
0 |
|
绛 |
(1,0,1) |
|
0 |
|
白 |
(1,1,1) |
|
0.1 |
注：假设
B,G,R的最大值是1。
表示1超出B,G,R最大者的那部分,
即
[B G R ]= 1-max(B, G, R)
[B G R ]= min(B, G, R)
同时我们有颜色分解定理：任何一种颜色总可以写成：
＋
(0,1,0)+
(1,1,0)+
＋
(1,0,0)+
(1,0,1)
＋
(1,1,1)
并且右边最多三项不为零，而且三者必然在图中某个扇形的三个定点上。
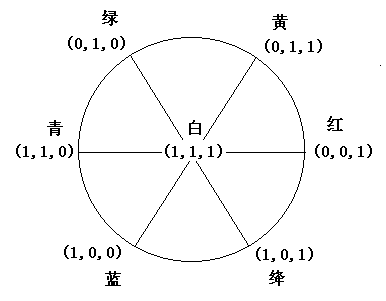
图
10 任何一种颜色总可以分解为一扇形三定点上的三项证明是简单的：因为
R,G,B按大小排列有6种次序，每个扇形反映一种次序。 这一模型之所以叫译码模型是因为，其逻辑运算很象数字电路中选择地址用的三八译码器中的逻辑运算。假如我们令上面的B,G,R的取值要么为0，要么为1，那么，B,G,R和8种颜色信号的关系就是3－8译码器的输入输出关系。表1 B,G,R和8种颜色信号的关系正好是3－8译码输入输出关系
|
BGR |
黑度
|
红度  |
黄度 |
绿度 |
青度 |
蓝度 |
绛度 |
白度 |
|
000 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
001 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
011 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
010 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
110 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
100 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
101 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
111 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
上面分解公式可以写成：
这里,
,
,
是三个非0项中的三个基矢,
且=(1,1,1);
,
别是相应,的输出码的系数或其大小。
是白度(白的程度)。假设和所在的角度分别为
和,
令
θ、 rc、 z、 rs
便分别代表(B,G,R)的色调(hue)、 彩度(colourfulnes)、明度 (brightness)和饱和度(saturation)(如果B,G,R是光谱三刺激值X,Y,Z通过 适当的线 性和非线性变换得到的)。根据译码模型, 明度、彩度、白度 ( whiteness)、 黑度(blackness)和B,G,R之间的关系如图三所示, 图中 med(B,G,R)是B,G,R 中中间的一个或第二大者。
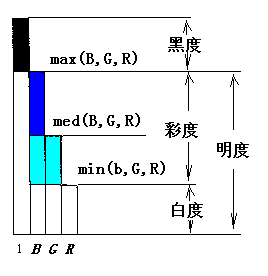
图
11 白度，黑度，彩度，明度图解Alvy Ray Smith等人从电脑绘图的角度，研制了类似转换。不同的是，它们那里主要考虑的是应用， 而不问色觉产生的心理过程，也没有讨论和采用逻辑运算，而是通过带有许多条件判断的程序达到类似目的
。笔者的模型除了上述不同，最重要的不同之处是提贯彻了阶段模型中的思想，提出了新的互补处理运算――而且这一运算非常巧妙。我们用文氏图说明互补处理的本质。 令∪、 ∩、'代表并、 交、补三种集合运算,B、G、R分别代表三个圆形区域(见图4)。为 了方便, 我们也用 - 作为补运算, 并且有时省去∩。
图4 显示互补处理本质的文氏图
于是
...可分别表示三个圆圈划分出的8个
区域。
从B,G,R, 我们首先得到
它代表B,G,R,中两个或三个相交的区域。 然后我们由B和M作逻辑减得到蓝色和黄色区域：
由G和M得到绿色和绛色区域：
由R和M得到红色和青色区域：
现在我们用B,G,R表示三接收器输出, 它们取值于集合［0, 1］。 集合运算被模糊准布尔代数运算∨、∧、
代替(∨表示取大,∧
表示取小且可省略，表示超出)。
下面计算惊人地简单。首先我们求出B,G,R三者中第二大者(包括并列最大和并列最小者):
M =med(B, G, R) =［BG∨BR∨GR］
or M =max(min(B, G), min(B, R), min(G, R))
然后分别用B,G,R减去M就得到互补信号:蓝-黄(
)、绿-绛(
)和红-青(
)：
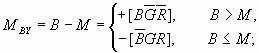
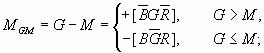
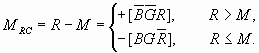
图
12 互补处理图解(横坐标：波长；纵坐标：信号强度)相应不同单色光的互补处理如图12所示。 我们也可以把图5上面的部分当做文氏图。 其中有8个划分的区域, 一垂直线在某一区域上的长度就是相应的单纯色信号的大小。 不同单色光引起的颜色视觉变化可由这些区域得到很好说明。
译码模型中互补处理的原理框图如图13所示。 为了演示颜色信号在视网膜和大脑皮层的处理, 笔者已经做出了一个完整的颜色视觉物理模型(参见图14), 它的运行正象期望的那样。
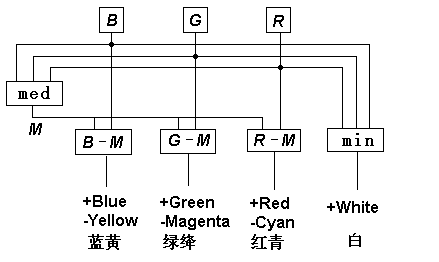
图
13 译码模型中的对称互补处理网上有很多人眼视网膜细胞结构图片,如图14所示。
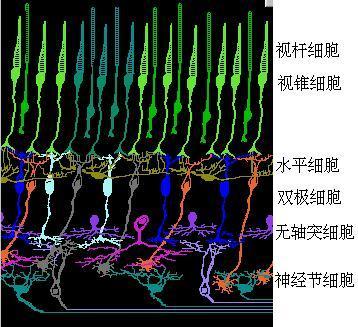
为了演示颜色信号在视网膜和大脑皮层的处理, 笔者制作了一个完整的颜色视觉物理模型(参见图15), 它的运行正象期望的那样。并且其结构和图14所示视网膜结构类似。
其中3DU是光电三级管, 它模拟视锥细胞; DA是差动放大器,它模拟双极细胞; LED是发光二极管, 它被假设为脑皮层上的色觉细胞; RE是电阻, 2DK是二极管。 左上角的二极管和电阻 阵列被假设为水平细胞, 它产生输出M=med(B,G,R). 按照流行的阶段模型，水平细胞的功能是很难解释的，而按照译码模型，对其功能的解释则简单明了。 双极细胞和视锥细胞数量相当，近于一一对应，在译码模型中是类似的。而在流行的阶段模型中，两者没有一一对应关系。
不同的是，上面物理模型没有考虑空间信息。神经节细胞输出不仅含有颜色信号，也含有空间信号。我以为视网膜中无突轴细胞可能是为了处理空间信号。如何处理，有待进一步研究。
上述物理模型认为: 在脑视皮层应有7种色觉细胞, 它们接收白色和六个单纯彩色信号; 大脑通过简单的加法运算得到明度和彩度, 通过求重心的方法产生色调。
