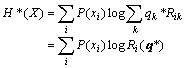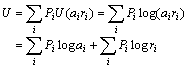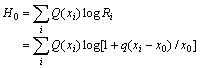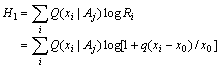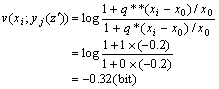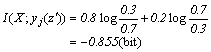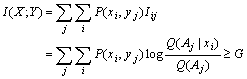从Shannon信息论到广义信息论

鲁晨光

--摘自《投资组合的熵理论和信息价值》(科大出版社1997)

 

本章先简单地介绍Shannon信息理论，然后将通信优化和编码优化作一比较——笔者以为这是很有趣的。本章后面的鲁氏广义信息论来自笔者的专著《广义信息论》[4]，但是严格说来，笔者的广义信息理论还应该包含下一章的基于增值熵的信息价值理论。之所以加上“鲁氏”二字是因为广义信息理论有多种，不加有暗中兜售私货或“篡位”之嫌。

1.1            Shannon信息论简介

1948年，美国工程师Shannon在贝尔实验室杂志上发表了长文《通信的数学理论》[7]，这篇文章标志着Shannon信息论或者说经典信息论的诞生。

经典信息论的诞生有两个来源，一是来源于物理学的熵理论。Boltzmann在讨论熵问题时就说过：熵是对失去的信息的度量。信息论中的熵H(X)和Boltzmann熵S存在某种等价关系(见《广义信息论》6.1节)。这说明了两者有血缘关系。

信息论的另一个来源是早期人们对电报通信的研究。自16世纪，Gilbert等人就研究了电报电码问题，这一研究的著名产物是Mouse电报电码。使用该电码可以用较少的电报符号传递较长的电文。而Shannon熵正反映了使用最优方式编码时，平均每个文字需要的最短码长。

Shannon通信模型如图1所示。

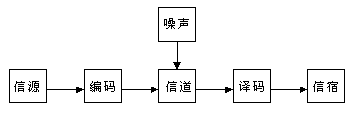
图 1  Shannon通信模型

有时我们把编译码部分和噪声并入信道，则通信模型简化为

信源®信道®信宿

我们用取值于A={x1，x2，...}中的随机变量X表示信源文字，用取值于B={y1，y2，...}中的随机变量Y表示信宿文字，于是信源和信宿可以被抽象为概率分布函数P(X)和P(Y)，而信道可以被抽象为条件概率分布函数P(Y|X)。

信源的熵是

       (9.1.1)

Y提供的关于X的平均信息量是给定Y时X的熵的减量，即

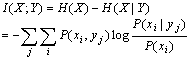            (9.1.2)

这就是著名的Shannon互信息公式；其中H(Y)是Y的熵，H(X|Y)是给定Y时的X的条件熵。给定Y=yj 时，I(X；Y)变为yj 提供的关于X的平均信息：         

         (9.1.3)

上式也叫Kullback公式。后面将说明，如果把P(X|yj)理解为预测的可能性测度，则I(X；yj) 就是预测和事实一致时的平均信息。可以证明I(X；yj)必然大于0。

Shannon 定义了两个重要函数：信道容量和保真度信息率。关于后者的理论后来又有所发展，并且保真度信息率被改称为信息率失真(information rate—distortion)[27]。信道容量和信息率失真分别是通信的数量和质量指标。如果把通信系统和生产系统相类比，则信道容量就相当于生产能力，而信息率失真就相当于给定产品质量要求时，单位产品所需要的最少劳动量。

近50年来，以Shannon理论为核心的经典信息理论在编码、检测等方面取得了巨大成就；然而，它远不能解决信息领域实际遇到的数学问题。这些问题是：怎样度量一系列颜色或图像实际给予的信息？感觉分辨率怎样影响主观信息量？相似事件而不是随机事件提供的信息如何计算？信源和信道可变时信息量如何计算……怎样度量统计数字的信息和信息价值？怎样度量语言、预言(比如天气预报)和谎言的信息和信息价值？将有不确定事件发生时，选择怎样的语句可以提供最多信息或信息价值？给定通信的主观效果和信息价值要求时，客观信息率或平均码长可能压缩到多少?

把Shannon理论应用于日常生活会得出非常奇怪的结果，这可以用一个例子来说明：有两个气象台，关于是否下雨，一个总是正确预报，而另一个总是错报；而根据Shannon理论，两者提供的信息是一样的，因为Shannon理论只看概率，不看语义。

关于Shannon理论的局限性，我们可以换一种说法：Shannon创立的经典信息论根本就不是关于我们日常所说的 “信息”的理论，它充其量只是通信编码理论。但是Shannon信息和日常信息也不是没有联系，后面我们将证明，Shannon信息是日常信息的某种特例——假设收信者完全了解预测者预测规则时的特例。

1.2            Shannon熵和Shannon互信息的 编码意义

使用电报通信的早期，人们用长短不同的信号表示所要传递的字母A，B，C，……。设长短信号分别用0，1表示，则一个字母可用一个0-1码，比如001表示。后来发现，用较短的0-1 码表示经常出现的字母，比如E；而用较长的0-1码表示较少出现的字母，比如X；这样就能在传递相同电文的情况下所用0-1码的总长度最短，或每个字母所用平均码长最短。然而，要想不失真地，即在H(X|Y)＝0的情况下，传递电报电文，平均码长最多能缩短到多少呢？Shannon理论告诉我们，这个平均码长的极限就是Shannon熵 (假设信源信号前后无关或者说信源是无记忆的)。

通信系统中平均码长公式是

      (9.2.1)

其中ci是为xi编码的码长，mi是长度为ci的码的变化种数，比如用0，1二进制数编码，对数以2为底，ci=2时，

有00，01，10，11四种变化。编码优化就是改变编码规则，使 最小。Shannon离散无记忆信源无失真编码定理告诉我们，当编码使得

     (9.2.2)

近似成立时，接近其最小值——它就是Shannon熵：

        (9.2.3)

比如要传递三个可能的文字a，b，c之一，它们出现的概率分别是1/2，1/4，1/4； 我们用0-1码编码，使平均码长等于Shannon熵的编码规则如表9.1所示。

表 0.1 平均码长等于Shannon熵的编码

文字

a

b

c

概率

1/2

1/4

1/4

编码

0

10

11

码长

1

2

2

如果各文字出现的概率不正好等于1/2，1/4，1/8，... 我们可以把相继的几个文字当作一个字母来编码(分组码)，使得平均码长无限地接近H(X)。

因为熵H(X)和H(X|Y)分别意味着Y提供前后，我们为X编码的最优编码平均码长，所以Shannon互信息I(X；Y)意味着因Y提供信息而节省的平均码长。可见Shannon熵和Shannon互信息有其客观性。

1.3            投资和编码比较

（ 省略）

　

1.4            投资渠道和投资容量——Shannon信道容量理论推广

（省略）

1.5            广义信息论研究背景

几乎每个领域都有把已有的正统理论奉为圣经，从而拒斥一切“异端邪说”的卫道士。下面我们向经典理论提几个问题，广义信息论的基本思想也由此体现出来：

1)      人（或动物）能否接收信息？人收到信息和更具体更正确地了解事实是不是一回事？

2)      通常人并不知道确切的事实发生的概率和条件概率，而只能根据经验、知识、语言、感觉或测量信号作主观预测，这时信息量如何求法？

3)      常识告诉我们，主观预测与事实相符且精确，所得信息就多，反之，信息就少，信息论如何与常识保持一致？

4)      实际的通信系统通常是开放的，人对于事实(即信源和信道)的认识总是处于进化之中，这时信息量如何求法？

人们常说，我们的时代正走向信息化时代；然而信息论落后于时代在今日是再严重不过了。虽然Shannon理论声名卓著，然而它所涉及的信息仅仅是日常语言所说的信息的一小部分，即被减小的随机不确定性。而对于语义信息、感觉信息、偶然事件及测量数据提供的信息，Shannon理论无能为力；甚至在经典通信范围内，信源或信道可变时，信息也不可度量。

实际上，任何一种通信都不能完全排除信号的意义问题。经典信息理论中讨论的信息率失真问题就和信号的意义密切相关。没有意义，哪来失真？由于避免考虑意义，经典的信息率失真理论就注定了残缺不全。失真实际上就是主观信息损失，因为不考虑意义，它就只能来自人为定义，而不是由统计确定；强调统计却反而导致统计的忽视。控制系统中的预测质量本来就应该用预测提供的信息作为评价标准，因为排除意义，预测信息就无法度量。

其实，曾和Shannon合著《通信的数学理论》[28]一书的W. Weaver在该书中的一篇论文中就提出通信的三个水平：水平A——通信的技术问题，如Shannon理论研究的；水平B——考虑到语义问题；水平C——考虑到效用或价值问题。

继Weaver之后，许多学者对广义信息作了不懈的努力，建立了各种各样的广义信息测度公式[4]，但是那些公式皆很难被理解和应用——如用于天气预报或股市预测。

笔者为了解释自己建立的色觉机制数学模型——色觉的译码模型——的合理性，从1988年开始研究感觉信息，后来又研究语义信息，继而建立了自己的广义信息理论。新的广义信息测度既和常识吻合，也是Shannon信息测度的自然推广。笔者以为自己找到了人们要找的东西。

1.6            鲁氏广义信息论

1.6.1            集合Bayes公式和三种概率的区别和联系

设信源信号集合(或字母表)A＝{x1，x2，...，xm}，信宿信号集合B＝{y1，y2，...，yn}，X和Y分别是取值于A和B中元素的随机变量。已知P(xi)和P(yj|xi)可以求出反条件概率

     P(xi| yj)＝P(xi)P( yj|xi)/P( yj)         (9.6.1)

这就是Bayes公式，其中

        (9.6.2)

设有A中子集Aj，Aj的特征函数为Q(Aj|X)∈{0，1}，记X∈Aj 的概率是Q(Aj)，则

   (9.6.3)

 

我们记Q(xi|Aj)＝P(X＝xi|X∈Aj)，于是有

  (9.6.4)

上式中，我们也可以用Q(xi)代替P(xi)(用主观概率预测代替客观统计)。

上式是以集合为条件的Bayes公式，我们简称它为集合Bayes公式，Q(xi|Aj)是Aj中xi发生的概率。汪培庄教授提出的随机集落影理论把模糊集看作是清晰的随机集合的统计结果[29]，通过随机集合落影理论，式(9.6.4)可被推广到集合模糊时的情况，推广后的集合特征函数Q(Aj|xi)又叫xi在Aj中的隶属度。设谓词yj=“X在Aj中”，则Aj是A中使命题yj(xi)为真的所有xi构成的子集，Q(Aj)是谓词yj的逻辑概率，Q(Aj|xi)是命题yj(xi)的逻辑概率，Q(xi|Aj)是给定预言yj时预测xi发生的概率，即

Q(Aj)=Q(yj为真)

Q(Aj|xi)=Q(yj为真|xi)= Q(yj(xi)为真)

Q(xi|Aj)=Q(xi|yj为真)

鲁氏广义信息论中用到三种概率：

1)      客观概率——通常概率论所讨论的或Shannon信息论所涉及的概率是客观概率，或者说是基于频率解释的概率；

2)      主观概率——不是基于统计而是基于主观预测的概率，即Bayes学派理解的概率；

3)      逻辑概率——命题或预言被不同的人或在不同情况下判定为真的概率，即Carnap等人所讨论的概率。

我们以下雨为例说明三种概率的区别。

1) 由历年气象数据统计得到的某地某月某日无雨的概率为客观概率——即数理统计所使用的概率，后面有时也简称为概率，如P(xi)，P(yj|xi)等即是；

2) 预报员根据气象观察数据和理论(或听众根据预报语言)预测未来某天无雨的概率是主观概率，它有时也被称为可能性测度，后面的Q(xi)，Q(xi|Aj)等即是；

3) 给定天气或日降水量时，某一语句比如“这天有大雨”被听众判断为真的概率是逻辑概率，有时也被称之为置信度，后面的Q(Aj|xi)，Q(Aj)等即是。

前面两种概率通常被视为概率的两种互不相容解释，自概率论诞生以来就有；而在广义信息论中，这两者是互补的。

值得注意的是，语句yj同时具有客观概率即语句被选择的概率P(yj)和逻辑概率Q(Aj)，两者一般不等；前者是纯客观测度，后者和主观理解的语义有关。比如某气象台一年到头总是报“无雨”，则选择概率P(“无雨”)=1，而逻辑概率Q(“无雨”为真)则和“无雨”的语义有关，而和语句被选择与否无关；经验告诉我们，它约为0.8。

P(yj|xi)和Q(Aj|xi)，Q(xi|Aj)和P(xi|yj) 的区别同理。

 

1.6.2            广义通信模型和广义信息测度

广义通信模型充分体现了这样的思想：信息来自预测，信息的多少需要事实检验；越是把主观原以为偶然的事件预测为必然并且预测正确，信息就越多，否则信息就越少甚至为负值。根据这种思想，最一般的信息是预言信息，其它信息都是预言信息的特例。这一通信模型和波普尔(K. R. Popper)的科学进化模式极为一致；同时也贯彻和深化了马克思主义的实践检验真理思想；Weaver的一些思想也由此得到贯彻。

关于知识或科学理论的进化模式，Popper认为，科学理论起于问题，为了解决问题人们提出假设，理论即假设；假设受到事实检验；如果根据假设所作的预测与事实相符，就说它通过了检验并在某种程度上得到确证；如果与事实不符，它就被证伪了；于是人们又寻求新的更加经得起检验的假说或理论；如此往复，以至科学进化。这种进化和生物进化是类似的。

下面我们介绍和Popper科学理论进化模式相一致的广义通信模型。

假设我们根据已知条件Z和知识K推出客观事件X 发生的概率或可能性分布Qk(X|Z)，我们称Qk(X|Z)为主观预测；这一预测通过语句Y间接表达出来。语言可能是自然的，也可能是人工的。再设事件集合A＝{x1，x2，...，xm}，语句集合B＝{y1，y2，...，yn}，观察数据集合C＝{z1，z2，...，zl}；X，Y，Z分别是取值于A，B，C中元素的随机变量。要度量的是Z或Y提供关于X的信息。下面我们用P(X)表示X的概率分布，用P(xi)表示xi或X＝xi的概率；其它同理。通信模型如图2所示。

我们以降水量预报为例说明该模型：Z表示气象数据，K为气象知识或理论；QK(X|Z)为气象台预测的各种降水量可能性分布(即概率预报)。Y是语句，比如“有小雨”，“有大雨”；Q(X|Y为真)是听众根据语义推出的降水量可能性分布。Q(X)是听众事先根据经验估计的降水量的可能性分布。

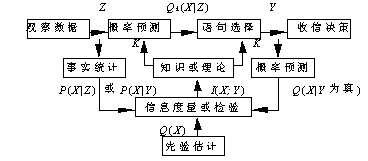
图 2   广义通信模型

检验知识K和预言Y的方法是看Q(X|Y为真)和Q(X)哪一个更与P(X|Y)相符，若前者更加相符，则预言有正的价值，若后者更加相符，预言价值为负。气象台为了提供更多的信息，于是就一再改进理论或推理方法，试图作出更正确且更精确的预报。如此反复，使预报和事实趋于一致。不光天气预报如此，疾病诊断如此，经济预测如此，各门科学知识的获得和进化也都如此。

由模型可见，最一般的信息是预言信息。下面是模型的几个特例。

1)      对于所有k，如果总有
              QK(X|zk) ＝ P(X|zk)
这表明预测和事实相符合，这时预言信息就变为描述事实的语义信息。

2)      如果没有语言表达环节，信息由Z而不是由Y提供，或Y和Z是——对应的，则预言信息就变为概率预测信息。

3)      如果既有1)又有2)，并且Q(X)＝P(X)，则这时预言信息就变为Shannon信息。可以说Shannon信息是客观信息，广义信息是主观信息，前者是后者在认识完全正确时的特例。

4)      当所有QK(xi|zk)∈{0，1}，或Q(xi|Aj)∈{0，1}时，表示预测的是确定事件。不过确定事件只是不确定事件的理想极限；即使物理定律，由于测量的分辨率有限及噪声干扰，用以检验的数据和理论预测的物理量都是更小范围内的不确定事件；所以，对于看似确定的物理事件，模型同样适用。

广义信息测度有两种形式，一个是概率预测信息，另一个是预言信息。后者可以通过集合Bayes公式转化为前者。首先我们看概率预测信息。

在上面的通信模型中，Z=zk提供的关于xi信息是(后面省去K)

          (9.6.5)

zk提供的关于X的平均信息是：                           

    (9.6.6)

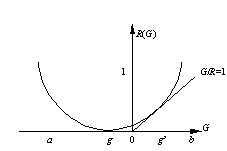
可以证明，即主观预测和事实吻合时，平均信息量达最大，这一最大值就是为Kullback信息。可以说上式是广义Kullback信息公式。广义Kullback信息可以通过图3中三条函数曲线的相似程度得到直观理解。

图 3  概率预测平均信息图解

通过式(9.6.6)可以证明：事实P(X|zk)一定时，若预测Q(X|zk)较之先验估计Q(X)更近于事实，则信息量为正值，反之为负值；Q(X)一定时，预测Q(X|zk)越近于事实，信息量越大。

对I(X；zk)求平均就得到概率预测互信息公式

    (9.6.7)

语义信息是类似的。对于语言通信来说我们一般并不知道P(xi)和P(xi| yj)，所能做的是根据经验和语义知道Q(xi)和Q(xi| yj为真)。因而我们要用语句的逻辑概率代替它的普通概率或选择概率。推广式(9.6.5)得到：当且仅当事实xi发生时，

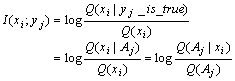      (9.6.8)

上式表明：

        预言或命题的信息量

=log(命题的逻辑概率/谓词的逻辑概率)

该公式将能保证：

1)        语句的先验逻辑概率Q(Aj)越小且后验逻辑概率Q(Aj|xi)越大，信息量越大，反之，信息量越小，甚至为负；

2)        语句越模糊，即Q(Aj|xi)和Q(Aj)越相近，信息量的绝对值越小。

下面从一个例子看上述公式如何和常识相符。股评家预测下个周末股市指数xi的涨跌。当前指数是1000点，下周末实际指数是848点。所有可能的指数集合是A，比如A=[500，1500]，A中有子集{大约900点}，{可能在800到1000点之间}等。表9.2中是一些数据和计算结果。其中Q(Aj)和Q(Aj|xi)来自常识。

　

表 0.2  股市指数预测的信息评价(指数实际上是848点)

　

Aj

yj(xi)

Q(Aj)

Q(Aj|xi)

评价

信息

　

 

(850点左右)

“指数将在850

点左右”

0.15

1

精确

2.74

 

(700—1000点}

“指数将在

800—950点”

0.3

1

较精确

1.73

 

(小于1000)

“指数是跌的”

0.5

1

较模糊

1

 

(500—1500点)

“指数可能涨

也可能跌”

1

1

极模糊

0

 

(大概大于
1000点}

“指数可能

是涨的”

0．6

0．6

错了

-3.32

　

　

显然，以上结果合乎常理。当预言不变，为yj=“指数X大约会是xj”时，预言信息随实际指数xi的变化如图4所示。

前面我们假定听者相信语句正确，如果不相信或不完全相信，则我们要用更加模糊的集合代替原来的集合。

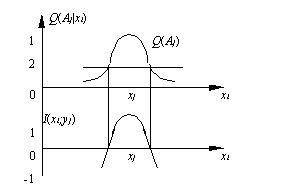
图 4  股市预言“指数大约是xj ”的信息

对I(xi；yj)求平均就得到度量语义信息的广义Kullback公式

     (9.6.9)

对上式再求平均就得到度量语义信息的广义互信息公式

  

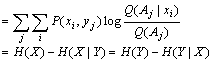  (9.6.10)

其中

        (9.6.11)

  (9.6.12)

分别是事实X的先验概率预测熵和后验概率预测熵，分别意味着当我们总是根据Q(X)和Q(X|Y)按照经典信息论提供的最优方式编码时，对X编码的平均码长，广义互信息I(X；Y)就正好是因预测而节省的平均码长；它可能是负的，这正说明预测不好会减少我们原有的信息。其中

         (9.6.13)

   (9.6.14)

分别是语句Y的先验和后验语义熵或模糊熵。它们具有限失真编码时平均码长意义[ 5]。

如果把信息量作为科学理论的进步标准，则我们可以得到如下结论：

1)     Q(X|Y为真)和P(X|Y)越是相近，则H(X|Y)越小，平均信息量I(X；Y)越大；这也就是说，理论解释或预测和事实越符合，则理论相对来说越进步。

2)     当H(X|Y)一定时，Q(X)和P(X)越是不同，I(X；Y)就越大，这也就是说越是能把原以为偶然的东西预测为必然，知识或理论就越进步。

3)     Q(Aj)越小而Q(Aj|xi)越大(对于所有j)，则I(X；Y)越大；这也就是说，命题或预言的先验逻辑概率越小，后验逻辑概率越大，相应的理论就越有价值；若两者总是相等，理论就是非科学的。

我们可以把一种感觉 (比如颜色感觉)或一个测量信号(比如秤的读数)yj 看作是一个模糊预测：“X大约是xj”，用Q(Aj|xi)表示xi和xj 的相似性或混淆概率，则上面的语义信息公式也可以用来度量感觉和测量信号的信息[4]。

广义信息测度和Shannon信息测度一样有编码意义，表示因预测而节省的平均码长。参看《广义信息论》。

1.6.3            广义信息测度用于预测、检测和模式识别的评价和优化

从广义信息论的角度看，许多信息传递或处理都有相似的过程(参看表9.3)。

对于表中信息传递或处理都存在一个评价问题。评价预测、检测和模式识别……的好坏，最简单的标准是正确率标准。但是正确率标准往往并不合理。比如，100个人中有两个人有爱滋病，甲大夫诊断全没病(爱滋病)，他的正确率是98%；乙大夫判断90个真没病的人没病，而称其它10人可能有病；他的正确率不超过92%。根据常识，乙大夫比甲大夫优，虽然他的判断的正确率低些。股市预测类似，假设有两个股评家，一个平常是对的，但关键时候——比如股市发生重大转折时——是错的；另一个相反。两相比较，可能后者提供的信息更多，对股民也更有用。有人看今天涨就预测明天涨，正确率肯定不低于60%，但是不提供任何信息；总是提供模糊的预测也能提高正确率，但也未必增加信息。由于Shannon理论的局限性，用Shannon信息测度度量检测、预测和模式识别的信息也往往并不妥当。Shannon 自己评价通信质量就不用信息标准而用损失(或失真)作为标准。然而，损失或收益又往往是主观确定的，缺少客观意义。均方误差似乎是一个较为客观的损失函数，然而它像正确率一样，不能体现对小概率事件的重视。用广义信息测度作为预测、检测和模式识别的评价和优化准则将更加合理。

　

^
　
表 0.3  广义信息的不同获取方式及相似性

信息获取
 方式

X

P(Z|X)

Z

Y(Z)

Y=yj=xj

Q

(X|yj为真)

语言交流

客观事实

了解方式

了解数据

语言规则

判断语句

主观理解

感官感知

物性(色光)

感官处理

感觉(色觉)

大脑判断

知觉(红)

认识依据

编码通信

信源信号

编码

编码信号

解码规则

信宿信号

行动依据

信号检测

信源信号

有噪信道

接收信号

检测规则

检测值

行动依据

序列预测

t时刻信号

前后关系

t以前信号矢量

预测规则

预测值

编码或行动依据

状态估计

t时刻状态

前后关系

t以前状态

估计规则

估计值

控制依据

天气预报

天气类型

观察

观察数据

预报规则

预报语句

听众理解

股市预测

涨跌

搜集情报

掌握数据

预测规则

预言

股民理解

诊断实验

疾病类型

实验方式

实验数据

判决规则

阴性阳性

医生理解

化学测试

化学成分

测试

测试数据

分析方式

分析结果

行动依据

模式识别

不同模式

特征抽取

特征矢量

识别规则

模式判断

行动依据

如果预言yj根据观察数据Z=z'作出，而且规则确定，即yj＝yj(z')，那么度量语义信息的广义Kullback公式变为

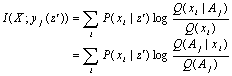   (9.6.15)

优化广义通信要解决的问题是：

1)      怎样用最经济的方法获得能含有足够信息的Z，即怎样确定观察P(Z|X)?(观察问题)

2)      已知客观信源P(X)和观察P(Z|X)以及广义信息量Iij＝I(xi；yj(z))，i，j＝1，2，...； 问提供怎样的判决Y=Y(Z)可传递最多信息?(判决问题)

3)      已知客观的P(X)和P(Z|X)，问选择怎样的判决语句Y，或收信人应如何理解Y才能使得I(X；yj(z))尽可能大？(语义问题)

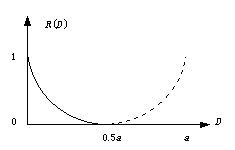
关于问题1)，对于股市预测就是搜集哪方面信息的问题，对于编码通信就是数据压缩问题，对于模式识别就是特征提取问题。经典信息论中的保真度信息率(或信息率失真)理论就是用来解决这一问题的。在鲁氏广义信息论中，取代它的是保精度信息率和保价值信息率理论(参10.4节)。

关于问题2)，可以利用广义Kullack公式。比如对于二元判决，观察者根据观察数据Z=z判定X是x0和x1中的哪一个，判定语句yj=“X大概是xj”，j=0，1。则应有

I(X；y0(z))>I(X；y1(z))

时给出判定y0＝“X大概是x0”，否则判定y1＝“X大概是x1”，于是推导出判决规则：在

         (9.6.16)

时判定“X＝x0”，否则判定“X＝x1”(其中I00=I(x0 ；y0(z))，其它类推)。

把式(9.6.16)中Iij换成损失或增益Cij，该式就变为经典的Bayes检测公式[27]。一般情况下，判决错误造成的损失比判决正确带来的增益大，广义信息量Iij也正好有这一特点。

对于股票涨跌或有病无病的判决，用后面的信息价值准则将更加合理。

关于问题3)，即语义问题，容易证明，当语句yj的选择或收信者对判决语句的理解使得Q(xi|Aj)=P(xi|z)，i=1，2，... 时，即预言不失真时，I(X；yj(z))达最大。这时应有

Q(Aj|X)/P(z|X)=常数

这意味着两个函数曲线形状分布相同时，平均信息量最大。

流行的模式识别要求判决给出若干个互不相容的模式中的一个，而广义信息准则则允许相容语句(比如“小雨”、“中雨”、“大雨”、“中到大雨”……)同时在被选之列。因为在概率预测P(X|z)模糊时，“中到大雨”之类模糊语句提供的平均信息可能更多[4]。

2.      信息价值、预测评价
      和经济学应用

已有文献提供过不少信息价值测度，但是这里提供的信息价值测度有明确的客观意义——它反映信息导致的的资金增值速度的增量。本章适于与信息和决策有关的理论研究者和学生阅读，也适合于从事机器预测和决策系统的研究者和开发者阅读；对理论不感兴趣的普通投资者可以忽略本章部分或全部内容。

2.1            基于增值熵的信息价值公式

曾和Shannon合著《通信的数学理论》一书的W. Weaver在该书中的一篇论文中提出通信的三个水平[ 30]：

水平A——通信的技术问题，如Shannon理论所研究的；

水平B——考虑到语义问题；

水平C——考虑到效用或价值问题。

由于习惯用法的原因，学说界谈及的“信息价值”不是指信息所值，而是指信息所产生的效用(utility)或效用增量。本书指的是效用增量，具体说来是投资效用的增量。

迄今为止，关于信息价值和效用的研究较为出名的学者是S. Guiasu和K. J.Arrow。Guiasu用加权熵公式[30]

        (10.1.1)

度量信息的效用，其中ui 是单位信息的效用。然而，如何确定ui ？U有什么实际意义？这些问题的存在使它很难实用。Arrow通过信息效用的分析给出了Shannon熵的信息价值解释，其问题我将在下一节讨论。

下面我们通过增值熵定义经济信息的信息价值。

设不同收益的概率预测矢量或者说概率分布是(Qi )=Q(X)=(Q1，Q2，...)，收益矩阵是(Rik )，则预计的增值熵是

        (10.1.2)

根据上式可以求出最优投资比例矢量q*，它是(Qi)和(Rik)的函数，即q*=q*((Qi)，(Rik))。当实际发生的收益概率分布是P(X)而不是Q(X)时，增值熵变为

     (10.1.3)

其中 

            (10.1.4)

当预测由(Qi)变为(Qij)＝Q(X|Aj)时，最优投资比例变为q**=q**((Qij)，(Rik))。我们把广义Kullback信息

   (10.1.5)

提供前后得出的增值熵的增量定义为信息价值(平均信息价值)：

                 (10.1.6)

可见和有类似结构。

对于上式，当xi 确定发生时，yj的信息价值变为

          (10.1.7)

它和单个语句提供的信息量公式形式类似。

不难证明，当信息大于0时，信息价值不会小于0；当信息小于0时，信息价值不会大于0；当信息增加时，信息价值不会减少。

不光信息是相对的，信息价值也是相对的。信息的相对性和收信者的主观理解及先验预测有关，信息价值的相对性还由于收益矩阵对于不同的投资人(能使用的投资工具不同)是不同的。比如，关于股市减息信息对炒股票和不炒股票的人来说信息价值不一样；关于股票下跌的信息对有股可卖和无股可卖的股民来说信息价值不一样。

2.2            和Arrow的信息价值公式比较

Arrow 定义的效用函数是[17]

    (10.2.1)

ri表示一种投资或打赌的第i种收益，Pi是相应的概率，ai是投资人在第i 种收益(而不是证券)上所下赌注占自己全部资金的比例，是第i种收益发生时，投资人获得的效用。Arrow认为用对数函数作为效用函数较为合理(在Arrow那里，采用对数函数不是因为几何平均收益)，所以有上式。

在的限制下，当矢量(ai)=(Pi)时U达最大，为

      (10.2.2)

而当投资人有了信息后，准确知道哪一种收益将要发生，从而将资金全部投到它上面时，有

            (10.2.3)

信息价值被定义为有无信息时投资的效用差，它正好是Shannon熵，即

    (10.2.4)

本人的信息价值定义继承了上述思想：信息价值被定义为有无信息时按最优比例投资产生的效用差。但是本人使用的投资模型与之大为不同。在笔者看来，Arrow 的投资模型是十分奇怪的。我们能够投资某一证券或项目，但是我们怎么能投资于一个项目的某种收益？式(10.2.1)要求每个ri都必须是正的(因为负数的对数无意义)，即任何时候都不存在亏损；通常的投资或打赌是这样吗？ri小于1会导致效用为负，这也令人费解。由于这些原因，Arrow的信息价值公式很难被应用。

在我看来，就投资模型来说，Markowitz是对的而Arrow 错了；但是就给定概率预测是否存在客观的最优投资比例来说，Arrow 是对的而Markowitz是错的。本书理论试图兼取两者之长，并使看来互不相关的信息论和投资组合理论在更高的层次上得到统一。

 

 

 

2.3            信息价值测度用于股市的预测评价和优化

在许多纯认识活动中，我们用广义信息测度评价预测是合适的；但是在许多和实践有关的活动中，用上面的信息价值测度评价预测才是合适的。下面我们说明如何用信息价值测度评价和优化股市指数预测。

令，给定(Pi )，求使达最大的概率预测Q(X|yj =y*)，y*就是最优预测。不难证明，()=(Pi )即预测准确时，平均信息和信息价值皆达最大。可能 yj 的选择范围有限，并不存在使(Qij)= (Pi )的预言。这时，使(Qij)最接近(Pi )的 yj 就

是最优预测。

例  股市指数X取值于指数集合A=[100，110，120，...]；关于X的预言集合是B={yj =“X将在 xj 附近”| j=1，2，...}；yj 的逻辑概率或xi 在 Aj 中的隶属度是，比如是以 xj 为中心，以为标准方差的山形函数：

           (10.2.5)

当前的指数是x0 ，先验概率预测是Q(X)(比方说是以 x0为中心的正态分布函数)；而事实是P(X|z’)。求预测yj=“X将在xj 附近”的信息价值及最优预测y*。

解  根据集合贝叶斯公式，有

    (10.2.6)

其中Q( Aj )是 yj (.)的逻辑概率。从增值熵

    (10.2.7)

我们得到优化比例q*(这里忽略资金成本和手续费)；从增值熵

       (10.2.8)

我们得到最优比例 q**。yj的信息价值便是

       (10.2.9)

对于每个 yj ，我们可以得到相应的q**。使信息价

值或后验增值熵

   (10.2.10)

达最大的 yj 就是最优预测y*。解毕。

上面的信息价值和最优预测的具体求解必须借助于计算机计算。下面我们用单硬币打赌模型模拟股市盈亏，从而使信息价值的计算更加简单实用。

例  设投资股市盈亏和指数涨跌相同。股民先验预测的盈亏是：

Fr1={0.7|-0.4，0.3|0.6}

股评家预测的是

Fr2={0.3|-0.4，0.7|0.6}

而实际股市指数是xi，下跌相对幅度是(xi-x0)/x0=-0.2，求：1)不可贷款且不可卖空时的信息价值；2)可贷款和可卖空时的信息价值。

解  1)根据Fr1，最优投资比例是q*=0；根据Fr2，最优投资比例是q**=1，信息价值是

2)根据Fr1，最优投资比例是

 

根据Fr2，最优投资比例是

信息价值是

解毕。

由上面例子可见：可卖空和可贷款时，预测不好带来的信息效用损失更大。

严格说来，假设收益呈二元分布是不合实际的，这使得实际收益不是二种收益中之一种时无法计算信息量(但不妨碍计算信息价值)。为计算上面例子中的预测信息，一种权宜之计是把实际收益(-0.2)的概率(1.0)按力学分解的方式分解为：P(-0.4)=0.8，P(0.6)=0.2，再用广义Kullback公式计算信息

2.4            从保真度信息率到保价值信息率

经典信息论中，通信质量用平均失真来度量。Shannon定义的保真度信息率(fidelity rate)就意味着在给定通信的质量要求时，信息传输速率最少需要多少。这就好象是：在生产系统中，给定产品的质量要求时，单位产品加工工时最少需要多少。

保真度信息率之所以被改称为信息率失真(rate—distortion)，主要是因为Shannon的“保真度”是用失真度来定义的。下面我们介绍信息率失真的定义。

假设对xi编码，解码出yj，yj相对xi的失真量是dij ，则Y相对X的平均失真量是

        (10.4.1)

设D是所要求的平均失真上限，PD是所有使d(X，Y)≤D的信道的集合，则信息率失真被定义为

         (10.4.2)

求R(D)函数的一般方法是在一些限制条件下，利用拉氏（Largrange）乘子法，改变P(Y|X)(反映编译码方法改变)，求Shannon互信息

   (10.4.3)

的极小值，限制条件是

       (10.4.4)

     (10.4.5)

由此可以求得R(D)函数的参量表示[27]。

下面仅以二元信源为例说明R(D)函数的性质。

设有二元信源，X，Y取值于{0，1}，d(0，0)= d(1，1) =0；d(0，1)=d(1，0)=a>0。R(D)函数为

  (10.4.6)

设P(x1)=P(x2)=0.5，H(X)=1，R(D)函数图像如图10.1所示。其中虚线部分是上面函数的一部分，由于经典信息论中信息不会是负的，因而对此不好解释，所以通常不画。而从广义信息论的角度解释则较为简单——要用谎言使收信者平均失真大于0.5a（或等于a），信息率也要大于0（或等于1比特）。

图 2.1  二元信源失真对称时的R(D)函数

在广义信息论中，通信质量是由主观信息量的相对多少来确定的，不仅和失真，也和逼真或信号的意义有关，所以我们用“保精度信息率”一词取而代之。信息率仍然指Shannon信息速率。取代失真上限D的是主观信息(即广义信息)下限G，限制条件之一改为

   (10.4.7)

由此求出的Shannon信息的最小值R=R(G)。 我们称R(G)为保精度信息率函数。

对于语言通信来说，编码就是语言表达，译码就是理解语义。日常语言交流中，我们常常用“五十多岁”而不用“五十岁零三个月”介绍或记忆某人年龄，用“六块多”而不用“六块八毛五”介绍或记忆某商品的价格，这是因为数字越精确(客观信息越多)越难记忆；用不精确的语言就是通过容易记忆的较少的客观信息得到足够的主观信息；或者说通过牺牲主观信息的绝对值来提高它的相对值。R(G)函数便是从量的角度给出了这种压缩客观信息方法的极限。

设上面的二元信源主观信息Iij 对称，I(1；1)=I(0；0)=b>0；I(0，1)=I(1；0)=a<0。于是推导出R(G)函数

      (10.4.8)

R(G)函数图像如图10.2所示[4]。

图 2.2  二元信源主观信息对称时的R(G)函数

       其中R(g)＝0意味着Y和X无关时，比如不了解事实胡乱判定时，我们仍然相信Y是X的正确响应，则主观信息损失的平均值至少为|g|比特。减少信息损失的方法是对靠不住的预言作模糊理解。一个典型的现实例子是：如果我们相信算命先生胡说八道，对事实就更加无知，信息就会有所损失，不相信就没有损失。

当G从g增大时，R也会增大，最大值为R(b)＝1， 这是易于理解的；当G从g减小时，R也增大；这意味着要想有意识地用谎言使收信者遭受信息损失(比如密码通信战中所希望的那样)，客观信息量R也要增大。

R(g')=G=g'，意味主观信息等于客观信息，这时信息效率G/R=1为最大。可见，像电路中有功率匹配问题一样，广义通信中也有信息匹配问题。容易证明，对于最佳匹配点，要求有主观预测和客观事实一致，即Q(X|Aj)=P(X|yj)(j=1，2)成立。

如果用信息价值代替广义信息作为评价标准，则有保价值信息率函数R(V)。R(V)函数图像和R(G)函数图像相似，只是未必有切点R(v’)=V=g’。R(V)函数可以为经济信息数据压缩提供理论依据。比如，预测一组证券中每个证券的收益时，可以把它们简化为二元分布(信息量少)，也可以把它们简化为三元、四元……分布(信息量多)。假设信息越多，得到预测和优化决策的计算工作量越大，成本越高。那么，究竟采用哪一种分布才既能保证有足够的信息价值，又不至于使预测和决策成本过高？保价值信息率函数将在理论上提供依据。

2.5            增值熵作为效用函数用于博弈

我们以市场进入为例说明不完全信息静态博弈[31]的效用评价。

在市场进入博弈中，一方是在位者，假设它有两种选择：默许和斗争；另一方是进入者，它也有两种选择：进入和不进入。如果在位者成本高，它会选择默许——因为斗争会两败俱伤；如果在位者成本低，它会选择斗争。不完全信息是指进入者不知道在位者究竟会选择哪一种行动，而只知道在位者具有高成本和低成本的概率P和1-P。表10.1显示了假设的两者的支付矩阵。第一对数“40，50”意味着高成本的在位者默许进入者进入时，进入者收入是40，在位者的收入是50。其它类推。

表 2.1  市场进入博弈的效用

 

在位者

 

      高成本

      低成本

 

  默许 

  斗争

  默许

   斗争

进入者     进 入

40，50

-30，0

 30，80

-30，100

       不进入

0，300

 0， 300

 0，400

  0，400

设P=1-P=0.5，进入者的净资产是100，则进入者进入的期望收益是

E=[0.5×40/100+0.5×(-30)/100]=0.05

不进入的期望收益是0。像通常那样用期望收益作为效用函数，则进入者应该进入。但是用增值熵作为效用函数(且不考虑资金成本)，则有

H=0.5log1.4+0.5log0.7=0.5log0.98<0

故进入者不该进入。用增值熵作为效用函数的同时考虑到了进入者的风险，因而更加合理。如果进入者的实力较强，其净资产是200而不是100，则有

H=0.5log1.2+0.5log0.85=0.5log1.02>0

故进入者应该进入。

以上方法可以推广到多方参与的博弈。假设第j个参与者预测其他参与者的行动的概率分布是P(X|z')，他采取的决策是yj，则使得平均效用

    (10.5.1)

达最大的决策yj =yj*就是最优决策。其中R(xi，yj)是自己采用决策yj而其他人采用xi (决策矢量)时自己的产出比。当每个参与人都采用这样的决策时，这样一组决策(y1*，y2*，...)就构成一个贝叶斯纳什均衡[31]。

       增值熵作为效用函数用于其它类型的博弈与此同理，不赘。

2.6            关于信息经济学

“信息经济学”在不同的地方含义不同。Arrow的一个论文集名为《信息经济学》[17]，其中有关于信息在经济领域中作用的讨论，涉及范围较广。可是按照信息经济学一词现在更经常的用法，它研究的是：委托人如何用金钱激励代理人或被雇佣者努力工作，以及如何解决被雇佣者或交易中知情的一方隐藏信息的问题[31]。因为这些研究涉及信息不对称——雇佣者不知道被雇佣者知道的东西，所以这门研究被称为信息经济学。

信息经济学特别是信息不对称理论的研究取得了非凡的成果，James Mirrlees和Willium Vickrey因此而获1996年诺贝尔经济学奖。我相信信息经济学在中国有其特别的意义。对于国有资产经营，国有资产管理局是委托人，厂长经理是代理人。正是由于国家对厂长经理们没有适当的奖罚制度，使得贪污腐败丛生。中国近年来发生的许多重大的机构亏损事件都和奖惩制度不当有关。亏了，个人不承担亏损，而赢了，个人可分得好处，这就鼓励了个人为机构交易时甘冒风险。信息不对称理论可以为制订适当的奖惩制度提供理论依据。

然而，令人遗憾的是，我们完全看不出目前的信息经济学和信息论究竟有什么关系。下面我们试图从熵理论的角度讨论问题，使得“信息经济学”看起来更像是信息经济学。

我们且以流行的信息经济学中委托——代理问题(参看文献[31]，397—447)为例说明。

委托人的问题是选择激励合同使得委托人的期望效用

         (10.6.1)

达最大，对于所有的a。其中a 是代理人选择的行动，p是产出值，s(p)是激励函数（确定激励合同），p-s(p)是委托人的收入，v(p-s(p))是代理人的效用，p(p|a)是代理人选定行动a时产出p出现的概率。同时代理人选择行动a ，使得自己的期望效用减去成本大于其它工作的平均效用，即

       (10.6.2)

(个人理性约束）

且a产生的效用大于其它任何行动a'产生的效用，即

      (10.6.3)

(激励相容约束）

在信息对称的情况下，委托人可以观察到代理人的行动或者说努力程度，因而可以制订强制代理人选择行动a的激励，使得后一约束失效。在信息不对称时，委托人无法确切了解代理人行动，使后一约束有效，或者说使代理人的行动有更大的选择余地。

现在我们用增值熵作为效用函数，则委托人的期望效用变为

   (10.6.4)

设委托人的净资产是g，则有R(p-s(p))=1+(p-s (p ))/w。类似地，代理人个人理性约束变为

   (10.6.5)

其中w'是代理人的净资产（包括劳动力折价）。这里没有把c(a)放在效用函数外边是因为效用和成本不是同一量纲。激励相容约束类推。

委托人从不了解到了解代理人的行动a时得到的关于产出p的信息(连续信源Kullback信息)是

     (10.6.6)

信息价值是

  (10.6.7)

其中s*(...)是信息不对称时的最优激励函数，s**(……)是信息对称时的最优激励函数。我们还可以把p(p|a)分为主观的和客观的，得到相应的广义信息和相应的信息价值。

上面表达方式除了使信息经济学更像是信息经济学，其好处还有：它可以通过净资产w和w'同时把委托人和代理人的抗风险能力也表达出来。

从上面分析可见，我们可以建立一个更广意义上的，或者说更加名副其实的信息经济学，至少它还应该包含本章前面几节内容，使得目前流行的信息经济学只是它的一部分。

2.7            有效市场理论有用吗？——为巴菲特辩护

（省略）

2.8            电子信息理论和经济信息理论的统一

经典信息论(电子信息理论的代表)的捍卫者(比如国际权威杂志IEEE Tran on Information Theory)以为只有自己研究的信息理论才是正宗的，其他的信息研究是“信息”一词不科学的滥用。他们拒绝对语义信息和信息价值的研究，把信息概念局限在一个远离大众的范围内。这在信息化时代逐步走近的今天显得完全是作茧自缚。经典信息论研究的信息和我们通常说的信息究竟有多大关系？我们先看看一些日常信息交流的例子：

作为股市期货投资者张三，他每天一早起来打开电视收看国际国内新闻和天气预报，想了解中国对外贸易情况以及天气对农产品的影响；然后他根据电视和报纸上的新闻对市场行情作出预测，再根据预测调整自己的交易头寸。晚上他看完财经新闻又坐在电脑前通过INTERNET网查阅有关上市公司资料和金属或农产品库存数据，然后又参加网上股市沙龙，在沙龙里痛斥某自称正确率达90%的股评家总是在关键的时候出错……

作为一个生产家电产品的公司经理李四，他每天要了解市场需求和竞争对手近况；他还经常看一大堆报表数据，以便控制成本和调整产品结构；他经常要考虑如何打广告，是选择电视还是报纸，费用压缩在什么范围内；他还要考虑如何对付竞争对手，是恐吓不行再让步还是坚决斗争到底……

作为一个经济学家王五，他研究信息在经济领域中的作用，研究广告的信息和信息价值问题，研究虚假信息对社会的危害及防范措施……

可是经典信息论研究的信息同张三、李四和王五……关心的信息有什么关系呢？可以说经典信息论充其量只不过是电子通信编码理论，根本不是关于大众所理解的信息的信息理论。如果国际权威的信息论杂志不违背地球上99.9%的人关于“信息”(information)一词的使用习惯或者说自然约定，它就应该把自己名称中的information换成别的的字眼，比方说communication coding (通信编码)或electronic information(电子信息)。

另一方面，哲学家、经济学家、计算机和情报工作者以及普通老百姓完全不理会电子信息论对“信息”概念的限制，他们按照传统的方式理解和应用“信息”一词。虽然他们不能用数学的方法来度量自己理解的信息和信息价值，但是这并不妨碍他们交流信息或赢得诺贝尔奖。

然而，经济信息理论的辉煌后面也包含了无奈。笔者不止一次听说过：没有哪们学科像经济学那样使用那么多先进的数学工具，也没有哪们学科像经济学那样没用；经济学家什么都懂，就是不懂如何赚钱。当然，这是言过其实的，但是也从一个侧面说明了目前的经济学理论不够实用。笔者以为缺少适当的度量经济信息和信息价值的数学理论是上述种种理论不够实用的一个重要原因。

虽然经典信息论或者说电子信息论在电子通信领域取得了辉煌的成就，但是要想在未来的信息化社会继续发挥重大作用，并且还把自己的理论称为信息论，那么它必须推广自己的研究范围和数学工具，必须解决老百姓通常碰到的信息，比如天气预报信息，股价预测信息，谎报军情信息……的度量和优化问题，必须解决经济信息和信息价值的度量，以及根据经济信息价值优化通信问题。

另一方面，经济信息理论虽然取得了辉煌的成就，可是信息和信息价值的度量这一基本问题却没有解决。由于缺少对经济信息(量)的数学定义，于是就导致了种种概念混乱。比如有效市场理论的信条“股票价格反映公司所有公开的信息”中的“信息”的用法就非常成问题，这里把公开的资料(文字数据)本身当作信息，而实际上，各人对资料理解不同，信息(量)就不同。

笔者相信自己建立的广义信息理论(包括本书的信息价值理论)已经初步实现了Weaver的设想——从数学上解决通信的后两个问题：语义问题和效用问题，从而也能解决一般的信息和信息价值的度量和优化问题。至少它在电子信息理论和经济信息理论之间架起了一座桥梁，使得两者可以使用相似的数学公式和优化方法。

笔者认为以Shannon理论为核心的经典信息论名不副实，但是这并不妨碍笔者对Shannon及其理论的敬仰。我以为捍卫一种理论的最好方式是发展它，推广它；使它的合理内核在新的、更加普遍实用的理论中得到永生。在Shannon理论问世50年的今天，我谨以自己的独特方式以示纪念。