第七章 信息 控制 生产
一个典型的控制系统,比如雷达火炮打飞机系统,主要含有这么两项工作[1]:(1) 根据测量数据估计系统的当前或未来状态; (2)根据状态估计施加控制手段。一个好的控制系统还必须对估计和控制作适当的评价和优化。
通常认为信息论和控制论相关是因为控制需要根据信息反馈作适当调整。Ashby等人的研究表明,Shannon互信息和N维互信息(见6.5节)还可以用于评价系统中变量之间的限制(constraints)或非独立性[2]。
第五章表明,广义信息测度可用第一项工作的评价和优化。然而,下面我们将看到,它也可以用于第二项工作的评价和优化。通信和控制之间的关系比常识或学术界目前认为的要紧密得多,微妙得多; 信息论中的一些优化理论同样可用于控制论。
通信分无噪声通信和有噪声通信——噪声来自电子干扰或语言的模糊性;同样,控制分确定控制和随机控制( 系统输入,输出响应是不确定的,只能用概率和条件概率表示)。我们要讨论的是后者,它更具一般性。生产系统或经济系统可
看作是控制系统的具体例子。
7.1 控制和通信的异同
通信是认识世界的手段,控制是改造世界的手段。通信或认识要求主观认识和客观事实符合,而控制或改造要求客观事实和主观理想符合。这就是通信和控制的根本差异。但是两者又都存在符合不符合和检验问题。信息测度便是检验标准,信息论中的一些方法和结论完全可以推广到控制论中来。
我们也可以把控制看作是信源来自主观要求的通信系统. 比如飞机设计蓝图是信源,实际制造出的飞机是信宿,制造工厂就是信道。对于邮件传送,信封上的地址姓名就是信源,信件到达就是信宿,邮局分送就是信道。
《系统和控制百科全书》[2]中称: 随着系统进化,在运行中减少关于有效控制的先验不确定性的控制为自组织控制。据此,人或机器人通过学习不断改进控制方法从而达到某种目的的控制就是自组织控制。也有人把图4.1.1 表示的认识进化过程叫做自组织控制过程[3]。这里我们仅讨论与认识进化相似但又不同的只涉及控制的自组织控制,控制模型如图7.1.1所示; 其中忽略了估计问题。
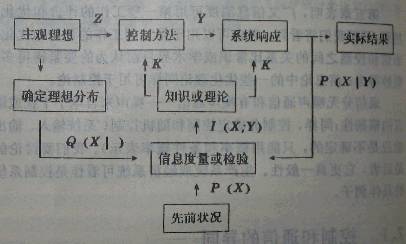
图7.1.1 与广义通信模型类似的自组织控制模型
图中表示,为使控制达到目的,需要根据知识K改变控制方法和系统的响应特性。
比如对于火炮控制,设打击目标的相对位置是X,控制方法或参量为yj; 使用控制yj希望炮弹达到位置的概率分布为Q(X|yj),过去控制中实际的炮火达到点的概率分布为P(X),有控制yj时的实际分布是P(X|yj),则广义Kullback信息
![]()
(7.1.1)
就反映了控制效果。较之通信中的信息测度公式,主观概率和客观概率的位置换了。和先验状况P(X)相比,控制结果P(X|yj)和理想分布Q(X|yj)越符合则I(X; yj)越大。若两者相等,则上式变为Kullback信息公式。
王身立曾指出负熵和合目的性的一致性,控制信息测度正好反映两者。
上述方法还可以用于温度控制评价,机械零件尺寸的控制评价,各部门占有资金相对比例的控制评价,结婚或死亡年龄的控制评价,生态的控制评价,饮料或土壤成分的控制评价,人才比例的控制评价,文章语句长短的控制评价…
若比较不同控制的优劣,只需计算
![]()
(7.1.2)
使H(X|yj)越小的yj越好。
若理想是确定事件,比如唯有xi使Q(xi|yj)=1,则I(X;yj)变为
![]()
(7.1.3)
这正是广义信息量公式在控制论中的表现(注意P和Q 在公式中的位置互换了)。这里P(xi|yj)和控制器有关,是一统计结果,不能因为偶然地xi相应yj发生就认为P(xi|yj)=1。
若理想有多种,Y可能取不同值,则控制关于理想的平均信息量就是
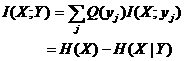
(7.1.4)
其中
![]()
![]()
这里不用P(yj)而用Q(yj)是因为控制任务是主观的而且是变化的。因为H(X)和H(X|Y) 分别反映了理想和现实的先验不一致性和后验不一致性,我们称H(X)为不一致熵或先验不一致熵,称H(X|Y)为后验不一致熵。在信息论中我们称H(X)为预测熵,现在我们也可以一律称之为不一致熵。
因为控制任务可变,假设P(Y)和P(X)是过去的Y和X发生的概率,Q(Y)和Q(X)是未来一段时间主观要求的Y和X发生的概率, Q (·)和P (·)一般不等。信息论中有类似情况。
我们称信息论的控制论推广为控制信息论。
7.2 熵H(X)的开关控制意义
我们且从两个例子看Shannon熵HS (X)的开关控制意义。
例7.2.1 邮局要按目的地把信件X分成M类,设第i类信件xi发生的概率是P(xi),每个工作人员将信件分为2类,问怎样安排分类可使信件平均被分类次数最少,最少达多少?
解 这里,分类就是控制,分类方法就是控制方法。分类也就是消除信件去向的不确定性,这一不确定性为Shannon熵HS (X)。每次消除的不确定性最多为1 bit ,故平均分类次数至少需要HS (X)次(HS (X)以bit为单位)。若每个工作人员将信件分为K类,则对数以K为底。
比如,要把信件分为三类,每人把信件一分为二; 三类发生的概率分别是P(x1)=0.5,P(x2)=P(x3)=0.25,K=2; 可使平均分类次数最少的分法是: 首先由一个人把x1和其他信件分开,再由一个人把其余两种分开。这样平均分类次数为
P(x1)×1+P(x2)×2+P(x3)×2=1.5=HS (X)
例7.2.2 要选择具有不同信号的M根电线中的一个,把它接通到一根输出线上去; 已知要接通第i根线的概率是P(xi),i=1,2,...,m; 设每个开关只能选择二中之一接通,问怎样接开关可使平均开关次数最少,至少有多少次?
本例和上例实质是一样的,所需开关数目的下限等于Shannon熵HS (X)的比特数。开关设置方法和离散无记忆信源无失真编码方法类似,不赘。
类似地,不一致熵意味着控制目标是Q(X)而我们按P(X)设置开关时平均开关接通次数的下限。
7.3 理想的集合表示及限误差信息率的控制论意义
现实中理想往往不是用某种概率分布而是用某个集合或模糊集合来表示的。比如,火炮要打击的目标是某个区域,医疗机构要控制的人的寿命的理想是近于七十或七十岁以上,某产品的尺寸的理想是在1-0.01和1+0.01米之间。
下面我们以火炮控制为例说明理想由集合给出时控制效果的评价。
设某次要打击的区域是Aj,它的特征函数为Q(Aj|X),则可以认为X的理想分布也就是给定Aj时X的反条件概率,为
Q(X|yj)=Q(X|Aj)=Q(X) Q(Aj|xi)/ Q(Aj)
(7.3.1)
其中
![]()
(7.3.2)
广义Kullback信息
![]()
(7.3.3)
就可以作为评价yj的信息标准。
当集合Aj模糊时,以上结论同样成立,只是Q(Aj|X)要变为模糊集合的隶属函数。
在通信中,给定误差限制求客观信息的最小值就得到限误差信息率。假设Aj={ A1, A2,..., Am}确定允许误差,则给定限制Aj求客观信息的最小值,我们可以得到控制的限误差信息率或限误差控制量
![]()
(7.3.4)
控制的限误差信息率的意义是:它表明适当安排控制开关(假设控制由二中选一开关完成),可在满足误差要求的情况下使平均开关次数近于或等于R(Aj)的bit数。如果不用开关控制,R(Aj)也反映了控制的复杂性或某种控制量的下限。比如对于火炮控制,如果用数字开关调节射击角度和方位,则R(Aj)就反映了一次射击平均需要的拨开关的最少次数; 如果用摇柄控制,R(Aj)反映了控制的复杂性下限。
7.4 信道容量和保质信息率的控制论推广
通信系统中,给定信道改变信源,求客观互信息的最大值就得到信道容量C; 给定信源和质量要求G改变信道求客观信息的最小值就得到保质信息率R(G)。对于控制系统也可以定义类似的函数。
假设yj和zk有一一对应关系,则yj同时表示第j种控制任务。我们称Q(Y)为控制任务,就象信息论中称P(X) 为信源一样; 称Aj为控制理想; 称反条件概率矩阵P(X|Y)为控制器,就象信息论中把条件概率矩阵P(Y|X)称之为信道一样; 同时称控制信息I(X;Y)为有效控制量,称IS (X;Y)为客观控制量。
一个车间可看作是一个生产系统中的控制器,产品生产就是控制,产品设计就是Aj,各产品产量就是控制任务Q(Y)。
定义7.4.1 给定控制器P(X|Y)和控制理想Aj,改变控制任务Q(Y)使有效控制量I(X;Y)达最大,我们称这一最大值为有效控制容量,记为C' ;给定P(X|Y)改变P(Y)使客观控制量IS (X;Y)达最大,我们称这一最大值为客观控制容量,记为C"。
C'和C"的求法分别和广义信道容量和Shannon信道容量的求法相似,只是X和Y对调了。
信道编码的方法在控制中就表现为围绕给定的控制器制定与之相匹配的控制任务和控制理想,从而充分利用控制器。控制容量C' 便提供了所能完成的有效控制量的上限; C" 意味着控制任务确定时,客观控制量( 或控制理想和控制结果一致时的主观控制量)的上限。
定义7.4.2 给定控制任务Q(Y)、控制理想Aj和有效控制量G改变控制器P(X|Y)使客观控制量IS (X;Y)达最小,这一最小值R为控制保质信息率。
信息论中限失真或限质量信源编码方法完全可以推广到控制中来。不同的是在信息论中我们要在给定P(X),Aj (即语义)和G的情况下时求使R达最小的信道P(Y|X),而在控制这里我们要在给定Q(Y),Aj和G的情况下求使R达最小的控制器P(X|Y)。X和Y位置互换了。
因为控制的广义互信息公式中Q(xi|Aj)和P(xi|yj)换了位置,控制保质信息率的求法与信息率失真的求法有所不同,怎样得到实用的求法有待进一步探讨。
通信中的主观分辨率在控制中就表现为控制的灵敏度。设对于每个xj存在一个yj,yj的控制能力可用一个模糊集合A'j表示,比如隶属函数为
![]()
d越小意味着控制的灵敏度越高,概率分布P(X|yj)=P(X|A'j)覆盖的范围越窄,Shannon条件熵H(X|yj)越小。
不难证明,给定理想时,灵敏度太高不好,太低也不好; 当灵敏度函数P(Aj|X)正比于控制理想Q(Aj|X)时,有效控制量I(X; yj)达最大。比如火炮射击的目标是某个较大区域时,射击精度太高反而不好。
通信中的分组编码(block coding) 方法在控制中就表现为利用自动控制方法。比如,在将信件一分为二的工作中,可把依次出现的四封信分为一组,根据出现的一组的地址( 可设想为0000,0001,...中之一)把它们分送到不同的自动机,每个自动机根据信件所在位置自动分类。这样,人工分类要做的只是把一组组信件分送到不同的自动机去,从而一封信的平均分类次数有可能大为减少。在理想事件序列存在规律性时,这种自动控制方法的有效性更加显然。
以Winer为首创立的Cybernetics通常被国人简称为控制论,而Winer的本意却是指人、 动物和机器之内或之间的通信和控制的科学[5]。看来广义信息论和已有控制理论的结合,更配冠以Cybernetics。
7.5 自由能公式 信息价值公式 生产价值公式
曾有人讨论过信息价值公式和物理学自由能公式之间的关系,并认为最大价值损失就相当于自由能[6]。下面结论不同——认为信息价值就相当于自由能增量。我的研究还表明,信息价值公式、生产价值公式和自由能公式,特别是和局域平衡自由能公式相似。这些结论不仅可以加深我们对三者的理解,而且提示我们把热力学中较为严格且成熟的公式推广到其他领域。
我们先看适于热平衡系统的自由能公式——它由Helmholtz(霍尔姆赫兹)提出,所以又叫Helmholtz自由能公式,即
F=U-TS
(7.5.1)
其中F表示自由能,U是系统内能,S是热力学熵;T是绝对温度,T的微观意义由下式看出:
![]()
其中k为Boltzmann常数,等式右边为分子在某方向上的平均平动动能。式(7.5.1)的信息论解释是:信息价值F等于最大可能(或熵为0时)的价值U减去有待获取的因减少熵得到的价值TS。当然我们也可以作控制论解释,把TS理解为需要通过控制或生产才能得到的价值。
式(7.5.1)的增量形式为
ΔF=ΔU-Δ(TS)
(7.5.2)
当ΔU为0,T为常数时,上式变为
ΔF=-TΔS=-kTNΔH
(7.5.3)
(参见6.1节)。令u=kT,u就相当于单位信息平均价值。对于各局域不等温系统,有
![]()
(7.5.4)
P(xi|yj)为第j个空间位置上第i种速度的粒子的相对密度。下面的P(xi)为温度平衡时粒子在第i种速度上的密度。设整体由等温到不等温且U不变时,自由能增量为

(7.5.5)
系统由平衡态到局域平衡态时,自由能增量为(参见6.2节)
![]()
(7.5.6)
其中A'为模糊集合,隶属函数为
Q(A'|xi)=exp(-εi/u)
Aj同理。可见自由能(增量)和信息价值有相同的本质。
把信息价值公式推广到生产系统就得控制价值或生产价值公式,其增量形式为
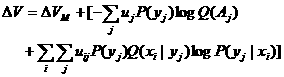
(7.5.7)
其中ΔV为价值增量,ΔVM为外部投资价值,Q(xi|yj) 是相应控制yj的理想分布(与热力学公式不同),uij是第j个分厂第i种产品的单位控制量的价值,uj同理。当ΔVM为0不变时,上式就和前面介绍的信息价值公式相同。
控制信息测度反映的是必要劳动量,可用开关次数作为尺度,因而也反映必要劳动时间; 而经济学中的产品价值也取决于(社会)必要劳动时间。可见上式有其道理。
当然式(7.5.7)目前也只有理论意义. 目的是加深我们对信息,控制,热力学和经济生产之间共同本质的理解。能否实用,有待探讨。
7.6 局域平衡自由能公式和投入产出价值公式类比
平衡热力学系统中的自由能公式微分形式有[7]
dF=dU-d(TS)
(7.6.1)
![]()
(7.6.2)
其中ui是第i种粒子的化学势,Ni是第i种粒子的组分,p是压强,v是体积,pdv是系统对外做功的微分。
对于局域不等温系统,有
![]()
(7.6.3)
其中
![]()
式(7.6.3)如果用于经济学,则它可被解释为
价值增量=投资+剩余价值(即控制信息价值)
对于局域平衡系统,式(7.6.2)变为
![]()
(7.6.4)
上式如果用于经济学,则它可被解释为
价值增量=实物数量变化引起的价值增量
-非生产支出
+单位控制量价值或劳动力价值改变
引起的价值增量
这就是经济学中的投入产出价值公式。式(7.6.4)中dnji 可被解释为第i个分厂中第j中产品或资料的增量,μji是相应的单价;其中最后一项增值可认为是由于技术进步引起的,比如新的冶炼技术使同样的有效控制量消耗较少的人的劳动量,从而为控制量Hj付出的价值降低; 引起这一项变化的另一个因素是μj ——可认为是单位劳动量价值——的改变。
通常的投入产出价值公式没有最后一项,加上它显然更加合理。通常第一项也分成几项写,比如写成:
产品价值-消耗材料价值+投资买来的产品或材料价值[8]
上面物理学公式如果用于经济学,则熵H表示广义熵,它反映产品加工前后的不一致性或加工所需要的必要劳动量。
无论如何,把热力学公式推广到经济领域得到的公式将不失一般性。不同的只是,经济系统中,即使是封闭的经济系统中,也并不存在热力学那样的熵增大趋势,比如至少我们的经济系统封闭于地球之上;剩余价值总是可能的。除非我们把热
力学熵也看作是经济学熵(即产品所需劳动量)的一部分。
经济学中的现象——封闭的经济系统中可以扩大再生产,创造更多的剩余价值——和热力学第二定律及流行的 Maxwell 妖解释(说封闭系统中不能增加任何自由能[9])是不协调的。
下面我们希望得到使两者更加相容的解释。
7.7 Maxwell妖的剩余价值解释
热力学第二定律可以说成是:不违反热力学第一定律的第二类永动机是不可能的。比如靠抽取海水中的热量发电不断做功是不可能的。多少年来,建造第二类永动机的努力的失败使人们更加确信这一点。然而,为什么这一定律成立? 为什么封闭系统中的熵只增不减? 一个合理的解释是概率论解释。
根据这种解释,封闭的热力学系统的熵减小不是不可能,而是可能性极小,要等几乎无穷长的时间。既然守株待兔地等待不行,把局部涨落一点一点积累起来行不行呢? Maxwell 妖[10]实际上就是这样一个保存局部涨落的机制。Maxwell 妖行不行? 似乎要捍卫热力学第二定律就一定要判定它不行。然而为什么不行呢? 似乎已成定论并且常被称道的解释是Brillouin的解释,说Maxwell妖为了看见分子需要用光子照射,这样它消耗的自由能就必然比它创造的自由能多,从而减小熵不可能。
说Maxwell妖需要看见实在是因为缺乏想象力。有色玻璃有选择地让光子通过并没有先“看见”。如果我们找不到其他更好的解释就只好相信这种似是而非的解释。可幸的是,概率的解释对Maxwell妖机制仍然有效。
假设Maxwell妖守住两个空腔之间的门, 空腔中装有快速和慢速两种分子,小妖让快速分子跑向左边,让慢速分子跑向右边。计算表明[11],即使小妖不消耗任何自由能,它哪怕是部分减少一克分子气体的熵仍然需要成千上万年时间。这主要是因为门也只有在适当的情况下才能开,即使按最佳尺寸确定门的大小(门开大了不好,开小了也不好),保存局部涨落也相当缓慢。从经济学的角度来看就是: 对于热力学系统,由于“生产资料”太差,单位时间内的剩余价值太低,以至于从宏观来看减小熵不可能。
以上解释和迄今观察到的所有事实都不矛盾。并能说明为什么热力学第二定律对于生物系统、经济系统这样的宏观系统不适用。另一方面,Maxwell妖的剩余价值解释也提醒我们:减小熵需要时间; 不经济地消耗会导致入不敷出,从而导致地球的荒废。
[1]〔美〕麦迪成 J S,赵希人译.随机最优线性估计与控制,黑龙江人民出版社,1984
[2]Conant R C. Information Laws of System,in: System and Control Encyclopedia,editor-in-chief M.G.Singh,Pergamon Press,1987,2493-2497
[3]Saridis G N. Self-organizing control system,in: System and Control Encyclopedia,editor-in-chief M.G.Singh,Pergamon Press,1987,4161—4165
[4]Fu K S. Leaning control system,In:J.T.Tou(ed) Advances in Information Systems Science, Plenum,New York,1969.
[5]Winer W. Cybernetics, MIT Press,Cambridge,Massachusetts,1948
[6]周炯磐.信息理论基础,人民邮电出版社,1983,337—343
[7]马本坤等. 热力学与统计物理学, 高等教育出版社,1980
[8]李茂林.经济数学方法,中央民族学院出版社,1989,271—291
[9]Brillouin L. Science and Information Theory,Academic Press,New York,1962
[10]Maxwell J C. The theory of Heat, London:Longman Greens & Co,1908,153
[11]鲁晨光. 为麦克韦妖辩护,长沙大学学报,6(1991),10—18