第六章 信息和统计
本章主要说明信息和统计物理熵的关系,以及熵增大定律和限失真及限误差信息率之间的联系; 同时将说明广义信息测度如何用于生物学和其他统计,并从信息论的角度解释熵增大定律。
6.1 信息和Boltzmann熵的关系
统计物理学中考虑大量粒子(比如分子)在其中无规则运动的系统,由此导出系统处于平衡态时,分子在不同能级或速度上的分布规律。
首先我们介绍相空间和相格[1]。一个粒子可能具有的空间位置要用三个坐标来描述,可能具有的速度也要用三个坐标来描述,这六个坐标所描述的空间叫相空间; 我们按某个很小的尺寸把相空间划为许多大小相同的六维立方体——相格,每个相格中粒子的空间位置和速度看作是等价的(即通过相格,建立划分相空间的等价关系)。给定粒子的一个分布{ N1,N2,...}( Ni是第i个相格中的粒子数),于是系统的微观状态数为
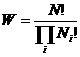
(6.1.1)
Boltzmann熵为
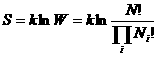
(6.1.2)
前人已经证明[2],使用Stirling公式
![]()
可得

(6.1.3)
其中HS是单位为.nat的Shannon熵, N是总的分子个数,Pi=Ni /N是任一分子在第i个相格中的概率。笔者还证明了对于每种Shannon熵HS (·),比如HS (X|Y),存在一个Boltzmann微观状态数W (·),使得NHS (·)=lnW (·)[3]。 现在我们用xi表示具有第i种能量的粒子。则所有具有第i种能量的相格的数目Gi为xi的简并度。这时有
![]()
(6.1.4)
粒子在具有第i种能量的相格上的先验概率为P(xi)=Gi/G ,后验概率为
![]()
则能量限制提供的Kullback信息为
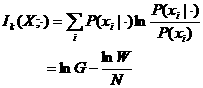
(6.1.5)
设系统分为n个局域,Y=yj表示粒子在第j个局域中,则有
![]()
(6.1.6)
于是信息和热力学熵S的关系为
![]()
(6.1.7)
若i表示相格的序数,则Gi=1,HS (Y)=lnG,S/(kN)就是Shannon条件熵HS (Y|X)。可见热力学熵具有Shannon条件熵的本质。
6.2 最大熵原理和限误差信息率的关系
由式(6.1.7)可见,最大熵原理和最小信息原理是等价的。在信息论中,给定失真,广义信息或信息价值时,最小信息可表示为限误差信息率。在热力学中有类似情况。
我们考虑平衡系统。设总能量为
![]()
(6.2.1)
其中εi为第i种粒子的能量。在总能量限制下,求使W或S 达最大的粒子分布(即最可几分布)。当xi表示第i个相格时,Gi=1,最可几分布为
![]()
(6.2.2)
其中Z是使Pi归一化的常数,即
![]()
β是待定常数,由热力学公式
E=F+TS
(6.2.3)
得β=-1/kT (T为系统的绝对温度,F为Helmholtz自由能)。
当i表示能级时,Gi>1,最可几分布为
![]() /Z
/Z
(6.2.4)
其中
![]()
解得β同上。这一分布规律已由实验检验。相应的熵为
![]()
(6.2.5)
对于局域平衡系统,有
![]()
(6.2.6)
现在我们从信息论的角度考虑。
对于每个局域给定一个能量Ej也就是给定n个误差限制集合:
![]()
(6.2.7)
在此限制下求得IS (X;Y)的最小值为
R(AJ)=H(Y)-H(Y|X)
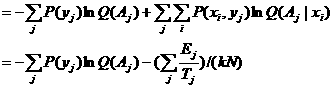
(6.2.8)
因为
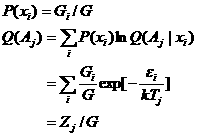
所以有
![]()
(6.2.9)
热力学系统更加象是控制系统。下一章讲到,在控制系统中,信息测度I(X;Y)反映的是控制工作量。从这一角度看,最大熵原理实际上是一条经济性原理——它意味着自然界总是以最经济的控制方式来响应我们施加的限制。
6.3 量子统计物理熵的信息论解释
现在考虑量子系统的物理学熵和信息论熵的关系。本节H (·)表示Shannon理论中的熵。
对于Bose-Einstein系统,系统的微观状态数为
![]()
(6.3.1)
熵为
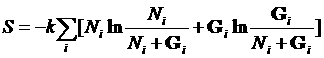
(6.3.2)
设X同上;z1为粒子,z2为相格; 我们称一个粒子或相格为“粒子-相格”; Z是取值于粒子-相格集合{ z1, z2} 中元素的随机变量。令
![]()
任取一个粒子-相格使得X=xi且Z=z1的联合概率是
P(z1, xi)=Ni /( N+G)
同理有
P(z2, xi)=Gi/( N+G)
给定Y时Z的Shannon条件熵为
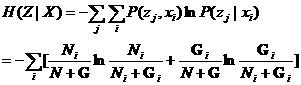
(6.3.3)
比较(6.3.2)和(6.3.3)得
S=k(N+G)H(Z|X)
(6.3.4)
在能量限制条件下对H(Z|Y)求极值,可得出该量子系统中粒子在不同能级上的最可几分布。
对于Fermi-Dirac系统,系统的熵为
![]()
(6.3.5)
改令z1为有粒子相格,z2为无粒子相格,其他不变,则有
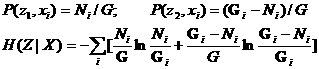
(6.3.6)
S=kGH(Z|X)
(6.3.7)
笔者本以为上述关系是自己的发现,现在知道B. Forte和S. Sempi早已发现了它[4]。
在(6.3.3)或(6.3.7)中设Gi>> Ni可得
![]()
(6.3.8)
比较(6.1.4)可知,对于平衡系统,上式中S和Boltzmann熵只差一常数。可见任一热力学系统中的熵(即在封闭系统中只能增大的熵)皆可用Shannon条件熵表达。这就使我们得到结论:
不断增大的热力学熵是给定能级的情况下粒子在相格中分布的Shannon条件熵。
因为Z和Y之间的Shannon互信息为
I(X;Z)=H(Z)-H(Z|X)
(6.3.9)
而对于封闭系统,H(Z)为常数,所以H(Z|X)增大等价于I(X;Z)减小。
理论上我们也可以建立平衡或局域平衡时量子统计物理熵和限误差信息率之间的关系,但Q(Aj|xi)不能直接解出。
6.4 建立在相似关系上的物理学熵公式
已有的物理学统计中用划相格的方法使相空间离散化,这和Shannon熵要求的是类似的; 这种方法假设相空间中任何两点要么完全相同,要么完全不同。而量子力学告诉我们,两个粒子占有的相空间位置可能部分相同部分不同。正因为如此,我们需要有一个和量子力学相一致的统计解释。
设相空间A中两点x和x'之间的相似度为Q(A'|x),A'为所有和x' 相似的点构成的模糊集合或模糊相格(不同相格可能部分搭接)。则X的广义熵为
![]()
(6.4.1)
其中p(x')为粒子密度。
若p(x)在x'附近的小范围内不变,即p(x)=p(x'); 且模糊相格A'的体积
![]()
不随x' 变化; 则
![]()
(6.4.2)
假设对具有同一能级εj的所有x',p(x')不变,从而Q(A') 也不变,则有
![]()
(6.4.3)
其中vj是具有能级εj的相空间体积。令Gj=vj/v,上式就变为和Boltzmann熵公式等价的熵公式(6.1.4)。较之(6.4.3),(6.4.1) 可以度量同一能级的相空间上粒子分布不均时的物理学熵,因而在理论上更具有一般性。至于模糊相似关系如何确定,是否可以利用波函数,能否得到新的结果? 有待进一步研究。
在(6.4.1)和能量限制下同样可以求出粒子的最可几分布(不赘)。对于量子系统可作类似处理。类似地,我们还可以求出H'(X|X)和H'(X;X); 它们是否有物理意义,尚不明了。
6.5 有序性 多样性 生物学统计
人们曾设想用信息测度或交互熵H(X;Y)表示有序程度。但是事情并非如此简单。对此我们稍加讨论。
有序可能发生在时间序列中,也可能发生在空间序列中; 事件的有序性也就是它们的规律性。根据常识,由前面事件的发生可以推断出后面事件的发生则过程有序; 比如,军号声比吵闹声有序,很好演奏的乐曲比胡乱演奏的乐曲有序。根据空间一部分事件的发生可以推断出另一部分事件的发生,则空间有序; 比如雪花比垃圾有序,楼房比山坡有序; 同时发生在时空中的事件的有序同理; 比如正常人的行为比精神错乱的人的行为有序,和平的社会比战乱的社会有序。显然有序和信息是相通的。有序还可能是因为事物之间的因果关系或控制关系,比如有组织的军队比乌合之众有序;老虎、鸡、虫和杠子之间一物降一物比谁也不服谁有序。下一章将说明控制效果也能用信息测度表示。
虽然度量上述信息一般是困难的,不过在理论还是可能的。比如对于时间中的有序性,假设Z=Xk 是过去一段时间内事件的序列,X是将发生的事件,两者之间的互信息或广义互信息就标志了序列的有序性(参见5.2节)。
对于空间比如一幅图象的有序性度量,我们可以这样做: 把图象划分成M个小块或象素,依次去掉不同的象素让观察者根据M-1个象素的样式或模式预测去掉的象素的模式; 预测将给予信息; 这样得到的平均信息即可作为图象的有序性尺度。为此,我们需要知道象素的各个可能模式及各模式发生的概率(可由已知的M-1个象素估计出)以及它们之间的相似性(可借助某种距离定义)。若去掉的象素xt (t=1,2,...,m)的模式是xi而预测为![]() 时,信息为
时,信息为
![]()
(6.5.1)
平均信息
![]()
(6.5.2)
便反映了该图象的有序性或 Prigogine等人说的“复杂性”[5]。
据此,模式越是多种多样(即Q(Aj)越小)而预测越是正确,信息越多,图象越有序。反之,模式多样但不可预测,或可以预测但模式单调(比如一张白纸,Q(Aj|xi)=Q(Aj)=1),信息皆为0,因而无序。
上面有序测度和观察尺度或象素大小有关,也和主观理解(或过去遇到的图象有关)。无论如何,用预测信息定义有序是合理的。度量有序方法的不定性是由于预测的方法和内容的不定性。换句话说,有序是有层次的,度量不同层次的有序性要用不同方法。
如果系统有N个参量X1, X2,...,Xn,则它们之间的有序性可由下面预测信息表示:
I(X2; X1)+I(X3; X1, X2)+...+I(XN; X1, X2,..., XN-1)
=H(X1)+H(X2)+...+H(XN)-H(X1, X2,..., XN)
(6.5.3)
若要度量主观观察到的有序性,I (·)应为广义互信息; 如果H (·)是 Shannon熵,该预测信息就是W. J. McGill提出的N维交互熵[6]; 进一步, 如果N=2,这一信息就变为互信息IS (X;Y)。
多样性和有序性有相同的地方; 但是多样性不要求事件相互预测。多样性测度可用自交互熵H'(X;X)定义。计算自交互熵只要求知道事件的概率分布和不同事件xi和xj之间的相似度Q(Aj|xi)=r(xi, xj)(参见3.8节)。
有序性和多样性测度对于许多非热力学统计都有意义。我们且以生物学统计为例说明。
比如,设有决定肤色和鼻子形状的两种基因X和Y,两者越是相关则互信息I(X;Y)越大; 据上面有序性定义,对于随机交配的种群或混血儿多的人群,基因更加无序。再比如,设动物X和动物Y总在相同地区出现,则两者互信息大,系统较为有序; 否则系统较为无序。在时间过程中,如果猫生猫狗生狗,儿女象父母,则过程有序;否则过程无序。显然,时间过程中的有序性也就是发展的稳定性。
王身立用信息论的方法分析生物统计很有启发。他有这样的看法[7]:
设某群体中某种等位基因(决定同一特征比如花瓣颜色) 有m种: x1, x2,...,xm, 给定基因出现的概率分布P(X),由此决定的Shannon熵HS(X)就反映了该等位基因的变异度。 设有不同群体:y1,y2,...,yn; 一基因属第j个群体中的第i种的概率是P(xi, yj),则联合熵HS (X,Y)大于各群体熵HS(X)的平均值。这意味着不同群体混合后随机交配产生后代时,基因的熵会增大,系统将退化。相反,自然或人工选择导致基因频率分布不均,HS (X)会减小,即负熵增大,意味着物种进化。
笔者认为,基因熵增大未必是坏事,就象百花齐放未必是坏事一样; 用自交互熵作为生物或生物种群的进化标准也许更为合理。
设Q(Aj|xi)是基因xi和xj 导致的生物特征相混淆的概率或相似度,则有
H'(X;X)=H'(X)-H'(X|X)
(6.5.4)
其中

自交互熵H'(X;X)就反映了基因的多样性或可选择性。不难证明,基因导致的特征(比如花的颜色)越是多种多样,H'(X;X)越大; 可见用H'(X;X)大小表示基因的进化或退化较好。广义条件熵H'(X|X)反映了基因的模糊性或相似性,H'(X|X)越大意味着各生物特征越是彼此相似,可选择性差,从而变化发展缓慢,应该说物种越退化。
上面只考虑某一种等位基因的进化和退化,若考虑某种生物的进化,则要用一组基因或生物种类代替单个基因。公式照样,具体方法类推。
另外,信息测度
![]()
(6.5.5)
可以表示某类生物xj中的一个的进化尺度; 据此,一个人越平庸就越退化,越象动物就越退化。要表示物种xj的进化尺度,或许可用MjH'(X; xj),其中Mj 是该物种的总重量或它所能控制的生物的总重量。据此,选择导致进化不在于基因熵减小,而在于xj的自交互熵H'(X; xj)增加。
按照上面公式,一物种越多并且越是与其他物种不相似,它就越进化; 一物种内部各个体(或等位基因)之间差异越大就越进化。因为随机交配往往导致特征折中化,从而模糊熵H'(X|X)增大,交互熵H'(X;X)减小; 所以H'(X;X) 同样也可以反映随机交配导致的生物退化。因为不同种群之间的有选择交配往往能产生新的有特色品种,因而容易导致生物进化。
我们也可以用类似的测度作为经济、文化、物产、人才…有序和进化的尺度。设xi表示行业,P(xi)表示行业xi占有资金的比重,Q(Aj|xi)表示行业xi和xj的相似性; 则H'(X;X)便反映了社会经济的繁荣程度。
一个好的系统应该既稳定又进化快,即既有序又多样。不过这两者又往往是矛盾的,不能片面追求。
6.6 互信息减少定律——熵增大定律修正
近些年来,熵的统计方法已被用于生物学、生态学、气象学、经济学、教育、农业等众多领域。然而,究竟哪一种熵是热力学熵或在封闭系统中不断增大的熵? 是不是熵增大就一定不好?
由于信息论对熵概念的发展,简单地说熵增大往往会导致混乱。比如张学文提出的物理场熵就不是增大的而是减小的[8]。有人主张禁止“熵”的非热力学用法。这实在是一种倒退。王身立说得好: 熵的概念和盐的概念类似; 盐一开始指食盐氯化钠;后来人们发现很多化合物和食盐有相同的本质,于是推广了盐的概念,统称这一类化合物为盐;熵的概念是一样的,推广是发展的需要[9]。
D.莱泽提出自然界中潜熵减去实熵等于序熵[10],张学文提出复杂性守恒(有序度加混乱度等于丰富度)[11],王身立提出熵和负熵互补[9],虽然说法不同,但是实质相同,如互信息公式(6.3.9)所述。为此,我们有必要把熵增大定律修正为互信息减少定律。这一修正既是为了避免概念混乱,也是出于看法的改变: 信息减少是自然以最经济的方式适应某种限制的结果。
有人说,自然界熵增大不好,熵减小好。 其实这是不对的。比如,地球如果没有太阳照射,虽然热力学熵H(Z|X) 会减小,但是潜熵H(Z)也会减小,从而I(X;Z)减小,即有序性减小,以至系统更糟糕。应该是: 信息熵或交互熵I(Z;X) 增大好减小不好。
从互信息减少的角度来理解张学文提出的物理场熵问题也很简单。物理场熵减小比如:一根铁棒一开始一头冷一头热,温度不均(温差均匀),铁棒与外界隔绝后,温度差渐渐消失。熵不就是变异度吗?按温差将铁棒分块得到的熵H(X)就是物理场熵。似乎怪异的是封闭的物理场熵不是增大而是减小了,好象与热力学第二定律矛盾。
如果我们把空间位置和温度看作两个随机变量X和Y,则物理场熵H(X)或H(Y)显然是X和Y之间的互信息I(X;Y)。只是因为
H(Y|X)=H(X,Y)-H(X)=0
于是有
I(X;Y)=H(Y)-H(Y|X)=H(Y)
用相似关系代替等价关系并用广义互信息公式也可以求出物理场熵I(X;Y),并且能考虑到分辨率的模糊性,在理论上更加可取。
至于熵增大定律能推广到怎样的范围,下一章讲到。
第六章参考文献
[1]高洪伯. 统计热力学,北京师范大学出版社,1986,16-52
[2]Jaynes E T. Information and statistical mechanics,Physical Review ,4(1957),620-630
[3]鲁晨光.信息熵和统计物理熵之间的关系,全国第三次熵与交叉科学研讨会论文(1991年10月攀枝花)
[4]Forte B & Sempi C. Maximizing conditional entropies: A derivation of quantal statistics, Rend. Mathematica 6(1976),551-566
[5]〔比〕尼科里斯,普利高津. 探索复杂性,四川教育出版社,1986
[6]McGill W J. Multivariate information transmission,Psychometrika 19(1954),97-116
[7]王身立.耗散结构向何处去——广义进化与负熵 ,人民出版社,1989
[8]张学文. 物理场熵自发减小现象,自然杂志,9,11(1986),847-850
[9]王身立. 正负熵互补原理,全国第三次熵和交叉科学研讨会论文(1991年攀枝花)
[10]〔美〕莱泽 D. 宇宙中序的增长,董春雨译,国外自然科学哲学问题,中国社会科学出版社,1991,216-236
[11]张学文. 论复杂性,全国第二次熵和交叉科学研讨会论文(1989年兰州),中国社会科学出版社,1991,216-236