第五章 通信优化
Shannon理论的意义主要就在于可以指导通信编码。广义信息论不仅对通信编码，而且对预测、检测和估计的优化都有实际意义。
按照常识，对于预测、检测、估计以及模式判别的好坏，用信息标准评价是合理的。由于Shannon信息测度的局限性，经典信息论在评价这些工作的时侯恰恰不用信息标准。这是耐人寻味的。
5.1 信源预测无失真编码定理
由3.7节我们已看到，预测熵H(X) (即HF(X))是预测信源Q(X)和实际信源P(X)不一致时，按预测信源Q(X)编码时的平均码长下限。由此很容易得到预测编码定理:
定理5.1.1 当预测Q(X｜Aj)(j＝1,2,...,n)和事实P(X｜yj)不一致时，而我们按预测为X编码,则平均码长L可以无限地接近X的广义条件熵
即存在编码使得
H(X｜Y)＋ε≥L≥H(X｜Y)
(5.1.1）
设无预测Y时按Q(X)为P(X)编码，则因预测而可能节省的平均码长就是广义互信息
I(X;Y)＝H(X)－H(X｜Y)
证明 给定Y＝yj时，根据定理3.7.1有平均码长Lj使得
H(X｜yj)＋εj≥ Lj≥ H(X｜yj)
其中εj使得
对不等式两边求数学期望便得到(5.1.1)。又因无预测Y按Q(X)编码时，平均码长下限是H(Y)，所以节省的平均码长是I(X;Y)。
证毕
显然，当预测和事实符合时,有L近于HS (X｜Y)(X的Shannon 条件熵);节省的平均码长是Shannon互信息。
到此，对于负无穷大信息也容易理解，这就是: 如果我们按完全错误的预测编码,平均码长就会增加到无穷大。广义互信息公式的编码意义可由本章后面内容进一步看出。
5.2 用广义信息准则代替预测的均方误差准则
为了说明预测评价的信息标准的客观性，我们先看看预测编码。
通信中，比如语音通信中，我们需要给数字序列编码，使得平均码长尽可能短，而且在接收端译码时没有失真。
一种有效方法［1］是根据第t个信号xt前k个信号xt-1，xt-2，...，xt-k预测第t个信号xt，用预测值
和实际值之差Δt＝xt−代替xt发送出去，接收端使用同样的预测规则算出t，再根据接收到的Δt算出xt＝＋Δt(见图5.2.1)。因为Δt的变化范围较小，它的Shannon熵一般小于xt的Shannon熵，所以编码的平均码长较短。
图5.2.1 预测编码
我们希望有一个好的预测规则。然而评价预测质量或预测规则的标准是主观选择的。流行的是均方误差准则，比如对于线性预测,设
＝a1 xt-1＋a2xt-2＋...＋akxt-k
(5.2.1)
使
(5.2.2)
达极小的系数a1, a2,..., ak就最为可取。其中T是实验序列长度,t从0到T变化。用拉氏乘子法，令f对每一个ar (r＝1,2,...,k)的偏导数为0,可得k个方程
(5.2.3)
由此可解出a1, a2,..., ak。
按照这一准则，把一个很偶然发生的信号预测准了和把一个必然出现的信号预测准了，评价同样。这和“无过便是德”的用人标准是一样的，它鼓励的是保守预测而不是提供更多信息的预测。联系天气预报可以更清楚看出这种评价方法的不合理性。我们需要的是“功越大于过越有德”的“用人”标准，广义信息测度正是这样的标准。
如果我们用X表示xt，用Z表示矢量(xt-1, xt-2,..., xt-k)，记为Z＝xk，用Y表示; 则预测信息就是Y和X 之间的广义互信息。Q(X)＝P(X)时，它可能达到的极大值就是Shannon互信息，或Shannon序列信息; 即
I(X;Y)＝H(X)－H(X｜Y)
≤HS (X)－HS (X｜Z)
＝HS (X)－HS (X｜Xk)
(5.2.4)
通常称上面信号序列相关过程为k阶马尔柯夫过程，它由条件概率P(X｜Xk)确定。
由上面的预测编码定理我们看到，用广义互信息作为预测评价准则和缩短平均码长的目的是完全一致的。只是它要求的是模糊预测。比如，我们把yj看作语句“X大约是xj”或“X∈Aj”(Aj是模糊集)，由Q(Aj｜X)和Q(X)可以推出Q(X｜Aj)，根据预测Q(X｜Aj)对X编码可使平均码长缩短为H(X｜Y)。
考虑从1到T的序列信息，广义互信息变为
(5.2.5)
设Q(Aj｜X)为钟形函数，即
(5.2.6)
yt来自式(5.2.1)所示预测; dt来自下面线性预测:
dt＝b1xt-1＋b2xt-2＋…＋bkxt-k
(5.2.7)
令I(X;Y)对所有ar和br的偏导数为0，可得2k个方程
(5.2.8)
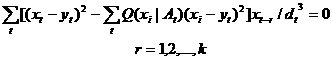
(5.2.9)
由此可解出2k个系数。设yt取值有m种，dt有m'种，则预测有m×m' 种。相应每一种预测使用一种编码方式是可能的。而直接根据预测P(X｜Xk)编码，则编码方式要有mk种，这一般是不可能的。不难看出，当dt不变且Q(X｜At)是正态分布函数时，方程 (5.2.8)就变为(5.2.3); 这就是说，根据均方误差准则选择yj是广义信息准则在上述情况下的特例。
一般情况下，解上面2k个方程是困难的。但是我们不妨先根据以往预测经验为每个yj 选取一个dj——让它等于预报yj时X的方差; 当我们作预测yt＝yj时就选择dt＝dj ，这样方程就简化为前面k个，编码方案一共只有m个。也可以使用迭代方法，依次确定两组系数br和ar。进一步简化，还可以假设Q(X｜At)也是正态分布，这时k 个方程复杂程度和采用均方误差准则时相近,为
(5.2.10)
上式体现了，如果dt或Q(At)较小时，即对于较确定的或小概率事件，同样报准了会有较多的信息，同样的误差将导致较大的信息损失，因而要给予更多的重视。
对于其它序列信号的预测，比如降水量、产量、需求量的预测，以及控制系统中系统状态参数的预测或估计，我们相信用广义信息测度代替均方误差作为评价标准会取得更好效果。
5.3 检测和估计的广义信息准则
在通信中，由于噪声干扰的原因，当发送的信号是X而接收到的信号会是连续信号Z。比如X为0和1之一时，Z为0和1之间的各种可能值。通信的一个重要问题是根据Z判定X为Y( 即
)。由于噪声的原因,即使X离散，Z也一般是连续的。 如果X是离散的，则上述判决就叫做检测; 如果X也是连续的，则上述判决就叫做估计［2］。至于怎样确定判决界线,这就看我们使用怎样的的评价标准。
我们可以把估计看作是检测在n＝m为无穷大时的特例。下面只考虑检测。
经典理论中用得益或损失(简称损失)作为评价标准。比如对于每个xi，yj (即j)定义一个损失c(xi, yj)，使
(5.3.1）
达极小的判决就最为可取。
广义信息论也接受这一标准（但用信息价值而不是价值损失，正值表示价值增量，负值表示价值损失，参见后面5.10节）。然而c(xi, yj)如何确定,在经典理论中，只能依据经验;并且在大多数情况下用误判率或均方误差(对于估计或A是实数集合的离散化时) 作为价值损失。
基于和预测同样的理由，我们建议在大多数情况下（即不考虑信息价值的情况下）使用广义信息作为评价标准。这就是:使
(5.3.2)
达最大的yj就最为可取。其中Q(Aj｜xi)是xi和xj相混淆的概率或相似度(参见3.８节)，可用确定Q(yt｜xt)的方法确定。
上式和第四章讲到的天气预报选择最佳语句用到的公式或模式识别中选择最佳判别模式用到的公式几乎相同（只是这里m和n相等)，这是因为天气预报，模式识别和检测判决在本质上相同。
我们以二元信源为例说明Bayes检测在广义信息论中的形式
设X∈A＝{ x0, x1}，Y∈B＝{ y0, y1}，Z∈C＝(－∞,＋∞),经典理论中经过复杂推导［3］，得到的Bayes检测方法是: 当
(5.3.3)
时判定X＝x0 (即输出y0)，否则判定X＝x1。
令Iij＝I(xi; yj)，根据广义信息准则，应有I(X; y0)>I(X; y1)时判定X＝x0，否则判定X＝x1，即
也即
(5.3.4）
时判定X＝x0，否则判定X＝x1。
若考虑信息价值，我们只需用vij＝uijIij (参见5.10节)代替Iij (其中uij 是单位信息平均价值)。用-Cij代替Iij就得到经典Bayes检测［3］。可见上面公式推导简洁得多。
一般情况下，判决错误造成的损失比判决正确带来的增益大，广义信息量Iij也正好有这一特点，比如当
Q(x0)＝Q (x1)＝1/2
Q (A0｜x0)＝Q (A1｜x1)＝1
Q (A0｜x1)＝Q (A1｜x0)＝exp (－2)
时，I00＝I11＝0.817，I01＝I10＝－2.069。
可见经典理论要考虑价值损失的场合中有许多实际上是因检测正确和错误时信息增减不对称; 这些场合用广义信息量作为评价标准就够了，而无需考虑价值问题。
公式(5.3.2)不仅可用于A上相似关系模糊(即集合Aj模糊)时的检测,也适于A 上相似关系清晰时的检测。比如当A上关系清晰且为单点集——即Q(Aj｜xi)∈{0,1},且仅当i＝j时Q(Aj｜xi)＝1，则广义信息标准就变为误判率标准。
这时我们把log0看作一个误判单位,记为err,设K为有限正整数,于是有
log(0/K)＝log0＝1 err
Klog0＝K err
logK＝0 err
比如对于上例，如果
Q(A0｜x0)＝Q(A1｜x1)＝1
Q(A0｜x1)＝Q(A1｜x0)＝0
则I00＝I11＝0 err，I01＝I10＝1 err; 于是检测方法变为:当
P(x0｜z') > P(x1｜z'）
时，判定X＝x0，否则判定X＝x1。和经典理论中结论一致［3］。
5.4 广义信道容量
Shannon理论中把条件概率矩阵P(Y｜X)叫做信道，在广义信息论中我们称之为客观信道; 而把它和语义矩阵或Q(Aj｜X)(j＝1,2,...,n)放一起称之为广义信道。我们可象经典理论中一样定义信道容量。
定义5.4.1 我们称
(5.4.1)
为广义信道容量; 其中ＰC是各种可能信源的集合，
(5.4.2)
当Q(X)≠P(X)时，设使得
(5.4.3)
达最大的xi是x'，则当X恒为x'时，I(X;Y)有最大值，为
C＝I(x';Y）
式告诉我们，在广义信道一定的情况下，最出乎收信者意外的事件作为信源时可使收信者接收信息最多。由于事实上收信者总是不断总结经验，根据P(X)改变估计Q(X)，所以广义信道容量也会改变。
当Q(X)＝P(X)时，原则上可以利用拉氏乘子法，改变P(X)求I(X;Y)的极大值，得到广义信道容量。但是实际上求解非常困难; 在此不赘。不过下面结论很有意义:
定理5.4.1 当Q(X)＝P(X)时，广义信道容量小于或等于Shannon信道容量。
证明 设使I(X;Y)达最大的P(X)是P'(X)，广义信道容量
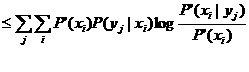
Shannon信道容量
(5.4.4）
证毕
5.5 限误差信息率及其和信息率失真的关系
第三章讲到广义熵的编码意义: 给定误差限制时，客观信息的极小值可用广义熵表示。这样，广义熵就有了客观的编码意义。不仅如此，误差限制还可以推广到限制模糊时的情况，并且模糊误差限制和经典理论中的失真限制存在某种微妙关系。
定义5.5.1 设P(Y)是信宿（纠正：应该考虑为信源），P(X)= Q(X)是信源（纠正：应该考虑为信宿）; Aj是yj 的误差允许范围，即把yj编码编作Aj中任一元素是允许的;则给定P(Y)和误差限制Aj＝{ A1, A2,..., An}时，改变P(X｜Y)求得的IS (X;Y)的极小值,记作R(Aj)，为限误差信息率。
R(Aj)和信息率失真R(D)不同，它对每个yj分别作了限制。比如要传递数据1,2,...,m，可能要求误差小于等于1，有一次传递误差大于1就不符合要求。
定理5.5.1 给定P(Y)和误差限制Aj，当所有集合清晰时，有
平均码长下限＝R(Aj)＝广义熵H(Y)
(5.5.1)
当其中有的集合模糊时,
平均码长下限= R(Aj)
(5.5.2)
证明 我们先用拉氏乘子法证明(5.5.1)。分析可知IS (X;Y)确有极小值。因
(5.5.3)
集合清晰时，限制条件为
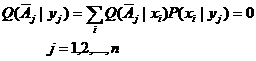
(5.5.4)
(5.5.5)
其中
是集合Aj的补集
的特征函数或隶属度。令
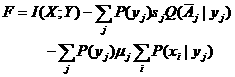
(5.5.6)
并且F对所有P(xi｜yj)的偏导数为0; 于是对于所有i, j,
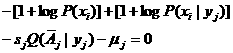
即
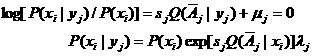
其中λj =logμj。因为对于xi∈Aj，Q(| xi)=0，所以
于是
(5.5.7)
又因
所以对于xi∈，
P(xi | yj)= Q(xi | Aj)=0
(5.5.8)
由(5.5.7)和(5.5.8)可得结论，当对于所有yj和xi，
P(xi | yj)= Q(xi | Aj)
(5.5.9)
时, IS (X;Y)有极小值. 将上式代入Shannon互信息公式得
(5.5.10)
我们把Q(| xi)看作失真量dij，则上面的R(Aj)就是失真限制D=0时的信息率失真R(D=0)。即
H(Y)=R(Aj)=R(D=0)
(5.5.11)
根据Shannon限失真编码定理可知，它们皆反映给定限制时编码的平均码长。
当集合模糊即Q(Aj | xi)∈［0,1］时，通过随机集概念(参见3.1节)，同样可以推导出: 当式(5.5.9)成立时，IS (X;Y)达极小，
(5.5.12)
证毕
不难看出，R(Aj)就是Q(X)= P(X)且预测和事实一致时的广义互信息。
设Y不变，为yj，我们记这时的R(Aj)为
(5.5.13)
现在我们来看限误差信息率和经典信息论中的信息率失真以及下一节讲到的保质信息率之间的联系。
在求率失真函数时，我们给定信源P(X)改变信道P(Y｜X) 求客观信息的极小值; 改变信道P(Y｜X)意味着编码方法改变。其实我们也可以给定P(Y)改变反条件概率矩阵P(X｜Y) 求客观信息的极小值; 改变P(X｜Y)意味着译码方法改变。后一问题也可以看作前一问题在Y是信源信号，X是信宿信号时的情况。
我们记给定P(Y)改变P(X｜Y)求得的IS (X;Y)的极小值是R'(D)，则
P(xi｜yj)=P(yj)exp(sdij)λj
（5.5.14）
时IS (X;Y)极小，其中
极小值为
(5.5.15)
现在我们把
Q(Aj｜xi)＝exp (sdij)，i,j＝1,2,...,m
(5.5.16)
看作误差限制集合,则λj正好等于1/ Q(Aj)。（５．５．１４）正好是集合Ｚ〗Bayes 公式。给定P(Y)和Aj求IS (X;Y)的极小值得到限误差信息率
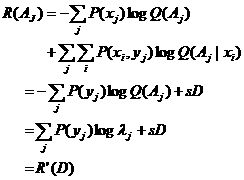
(5.5.16)
其中Q(Aj)正好等于1/λj (参见2.8节)。可见误差限制和失真限制存在某种等价关系，经典的信息率失真函数原来可以写成广义熵熵差的形式。
下一章讲到，统计物理学中的配分函数就相当于逻辑概率Q(Aj); 系统熵达最大时的熵值和限误差信息率存在简单联系。
5.6 保质信息率论——信息率失真论改造
改造信息率失真论［4］的方法是用广义信息量代替失真量求Shannon互信息的极小值。具体地说来就是用Iij＝I(xi; yj)代替失真量dij。假设要求广义互信息的下限为G，用G代替失真上限D；R仍然表示单位符号的Shannon信息;则经典的率失真函数R(D)就变为R(G)函数。我们称R(G)为保质(即保主观质量)信息率函数，它有类似的编码意义。经典理论中失真D只能是正值，而G可能是负值。
用与经典理论中类似的方法可得R(G)函数的参数表示:
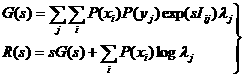
(5.6.1)
其中参数s等于dR/dG，是R(G)函数的斜率，它的物理意义是增加单位主观信息量时客观信息率R的增量。在信息率失真论中s总为负值; 而在这里它一般为正值，也可能为负值(参看图5.7.1)。
对于语言通信来说，编码就是语言表达，译码就是理解语义。日常语言交流中，我们常常用“五十多岁”而不用“五十岁另三个月”介绍或记忆某人年龄，用“六块多”而不用“六块八毛五”介绍或记忆某商品的价格，这是因为数字越精确，客观信息越多，越难记忆; 用不精确的语言就是通过容易记忆的较少的客观信息
得到足够的主观信息；或者说通过牺牲主观信息的绝对值来提高它的相对值。R(G)函数便是从量的角度给出了这种压缩客观信息方法的极限。
对于感觉或图象通信, R(G)函数更有其实际意义(见5.8节)。
在经典理论中，给定R求平均失真极小值，设极小值为D，则D(R)就正好是R(D)的反函数［5］。在广义信息论中有类似情况，不同的是，给定信息率R，既可以求得主观平均信息最大值Gmax(R)，也可以求得它极小值Gmin(R)
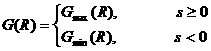
(5.6.2)
就正好是R(G)函数的反函数; 它告诉我们有限的客观信息最多可以传递多少正的或负的主观信息，有类似的优化通信意义。
由上节内容可知，给定P(X)和G等价于给定模糊误差限制:
Q(Bi｜yj)＝exp(sIij)＝［Q(Aj｜xi)/ Q(Aj)］s
i,j＝1,2,...,m
(5.6.3)
其中Bi是B上的模糊集，它是用xi为yj编码的误差限制集合。
5.7 具有相似关系的二元信源保质信息率函数
先以二元且具有相似关系的信源(即Q(Aj｜xi)＝Q(Ai｜xj))为例，说明保质信息率函数R(G)的性质。这时R(G)函数可直接解出。
例5.7.1 原图象象素有黑白两种x1, x2，有失真编码后译码得出的图象象素也是黑白两种，记为y1, y2，则Y会提供关于X 的信息，y1就相当于语句“X是白的”，y2类推。给定主观信息量
则可求出R(G)函数(可参考二元信源失真对称时的率失真函数的推导方法［5］)为:
设P(x1)＝P(x2)＝1/2; Q(X)= P(X);
可求得b＝0.817，a＝－2.069。注意广义信息量是不对称的。R(G)函数如图5.7.1所示。
图5.7.1 二元信源保质信息率函数
R(-0.626)＝0(如W1点所示)意味着Y和X无关时，比如不经测量胡乱判定时，我们仍然相信Y是X的正确响应，则主观信息损失的平均值至少为0.626比特。当然，如果我们知道Y和X无关,集合Aj就完全模糊，这一损失也就不存在。一个典型的现实例子是:如果我们相信算命先生胡说八道，对事实就更加无知，信息就会有所损失; 不相信就没有损失。
当G从W1增大时，R也会增大，最大值为R(0.817)＝1，这是易于理解的。当G从W1减小时，R也增大; 这意味着要想有意识地用谎言使收信者遭受信息损失（比如密码通信战中所希望的那样），客观信息量R也要增大。这也就是说，了解真情撒慌比不了解真情撒慌更可怕。
当s＝1时(如W2点所示)，有式(5.5.７)成立; 这时，R＝G＝0.473，意味着客观信息和主观信息相等。我们称
为信息效率; 则G/R反映了γ的上限，在W2点它达最大值，为1。
当Ｑ（A1| x1）= Q(A2| x2)=1不变，Q(A1| x1)= Q(A1| x2)变小时，意味着语义更加不模糊，W1将左移, W2将沿斜线向右上方移动。
5.8 保质信息率和信源量化等级及主观分辨率的关系
由于P(yj| xi)，λi和P(yj)三者相互依赖，只有特殊情况下才可直接求出R(G)函数(如上节所示); 一般情况下只能用迭代方法求出。具体步骤如下(后面皆假设Q(X)= P(X)):
0) 对于所有i,j，求出I(xi, yj);
1) 给出s起点，比如让s＝-10;
2) 假设R和P(yj| xi)的初值R0和P’ji，比如让R0＝100，P’ji＝P(xi);
3) 求出P(yj)和λi;
4) 算出新的P(yj| xi)＝Pji和IS (X;Y)＝R;
5) 令r＝｜R－R0｜/ R0，如果r>0.001(精度要求)，令R0 ＝R，P’ji＝Pji (i,j＝1,2,...,m)，转到3); 否则，算出主观信息G，输出s，R和G;
6) 令s＝s＋步长, 如果s小于终值，转到2)，否则结束。
我们通过一个图象通信的例子来看保质信息率函数的一般性质。
假设我们要把模拟黑白图象量化成数字图象，然后通过编码——传递或存储——译码，再将译码图象提供给观察者。译码图象的量化或灰度等级和原数字图象相同。为了方便，我们以图象上的一点——象素——为单位信号来讨论信息传递。优化通信需要解决的问题是:
1) 给定主观分辨率和主观信息要求时，为每个象素编码的平均编码数据最低可以压缩到怎样的程度?
2) 给定主观分辨率时，量化等级多少时，可使主观信息较多且信息效率较高?
我们先讨论前一个问题。
设原数字图象象素为信源。象素的灰度等级为X＝0,1,2,...,b(模拟图象可看作b→∞时的特例)，X的期望为c＝b/2，方差为σ＝b/8。令
归一化得灰度i的概率为
设译码后的象素的灰度等级是Y＝０，1,2,...,b。为了方便，假设灰度感觉也是Y; 并假设分辨空间均匀。分辨率函数为
其中d是分辨率参数，则d越小，分辨率越高。
图5.8.1 显示了b＝63时(未取更大是为了计算省时)，分辨率参数d和R(G)函数的关系。
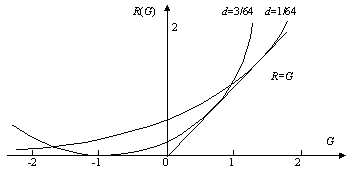
图5.8.1 给定量化等级b＝63时不同分辨率和R(G)的关系
结果表明:
1) d越小，或分辨率越高，R＝0的点G越小。这意味着，相信不含有客观信息的信号有信息，主观信息会有所损失，并且分辨率越高损失越大。比如,对原图象进行编码，编码后的图象和原图象无关(客观信息为0),如果我们仍然相信图象是对原图象的真实反映，则就有负的主观信息; 并且，分辨率越高，负的主观信息下限的绝对值就越大。
2) 分辨率越高，主观信息或G的最大可能值越大; 主观和客观达最佳匹配即G＝R时的G也越大——换句话说，要想提高信息效率γ，主观分辨率提高时，客观信息也要相应增加。
3) 当G接近最大可能值时，dR/dG很大。这意味着增加主观信息的绝对值要以降低主观信息的相对值为代价，这往往是不合算的。
4) 给定R时，存在最佳分辨率d，使G＝R。人脑就具有通过降低主观分辨率来提高信息效率的能力; 5.2节讲到由预测确定dt也就是调整机器的“主观”分辨率。
我们再看第二个问题。
图5.8.2显示了分辨率一定，d＝1/64时，R(G)函数和量化等级b的关系。
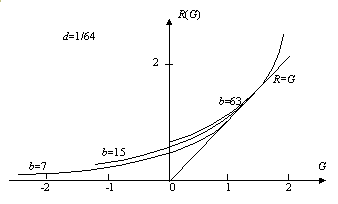
图5.8.2 给定分辨率时, R(G)和量化等极b的关系
结果表明，b较小时，b增加，G的最大可能值和匹配值(G＝R时的G值)增加明显; 而b渐大时，b增加对G的影响渐小。这就提示我们，分辨率一定时，量化等级过小不好，过大也不好; 过小则主观信息少，过大则不经济。
图5.8.3显示了s＝1,即客观信息和主观信息相等时，主观信息量和量化比特k＝log2(b＋1）及分辨率参数d的关系。
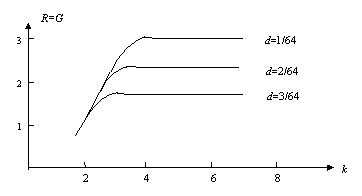
图5.8.3 s＝1时信息量(R=G)、分辨率及量化比特数之间的关系
结果表明，给定分辨率时，存在最佳量化比特数k'使得主客观匹配信息I达最大。当k小于k'时，信息I和k近似成正比，而当k>k'时，信息I略有下降之后便不再改变。下降的原因是:由于主观分辨率是模糊的，而机器量化归类是清晰的; k继续增大时，Q(Aj)不再减小从而先验特殊熵H(Y)不再增加，而后验广义熵或模糊熵H(Y｜X)则有所增加，以至信息减少。
5.9 图象视觉信息及通信优化
设由遥感图象可得n种色觉y1,y2,...,yn，这些色觉反映m种不同地物x1, x2,...,xm; 求一种色觉提供的信息可采用以下方法:
1) 采用集值统计或其他方法(见3.8节)确定模糊关系r(X,Y); 若设不同颜色反映不同地物，m＝n，则只需求模糊相似关系或分辨率函数Q(Aj｜xi)＝r(xi, xj) (i,j＝1,2,...,m)。
2) 由已有经验得到Q(X);
3) 对于每种颜色yj计算平均相似度Q(Aj);
4) 用广义信息量公式(见4.3节)计算出I(xi; yj)。
一种实用的计算平均信息的方法是使用广义自信息公式(见4.7.节),I(X;X)=H'(X;X)即为所求。
假设图象上各点的颜色是相互独立的，则可用广义自信息公式计算一点的平均信息量I(X;X); M行N列的图象提供的信息是I＝MNI(X;X)。如果各点相关，不同颜色反映不同地物，则理论上而不是实际上求图象信息方法是用矢量Xmn代替X求得I(X;X)。
关于彩色图象量化等级的选择，可以根据上节结论。不同的是要在三维颜色空间确定分辨率函数。一个较为实用的方法是: 先把三基色颜色空间变换为分辨均匀的心理颜色空间，比如θ-r-z(分别反映色调，彩度，明度)空间［6］，通过两种颜色在心理颜色空间的某种距离来确定模糊分辨率函数。
更细致的优化方法是把图象上不同位置或不同颜色的象素当做不同信源信号(可用5个参数表示)，把空间和颜色的数据压缩溶为一体。但是这要有更复杂的分辨率函数。方法类似。
关于彩色图象编码，参照5.2节，我们可以利用相邻象素颜色的相关性减少编码数据。对于时间过程中变化的图象,还可以利用象素时间前后的相关性。
5.10 信息价值 保价值信息率
有些信息重要，有些信息不重要; 信息相等而价值可能不同。比如天气预报提供关于风向的信息就没有关于晴雨的信息价值高。同样的信息，对于不同的人来说，信息的价值不同，比如关于海湾战争的信息对于有汽车和无汽车的人来说就不一样。
价值可能是金钱，也可能是人生幸福( 可以被定义为快感对时间的积分)。理想的信息价值的确定应使信息价值等于根据信息决策产生的价值增量，或者说，信息价值应等于决策价值。比如无某种信息时决策产生的价值是v1，有某种信息时决策产生的价值是v2，则信息价值应是v＝v2－v1。
因为一般情况下，信息越多，决策越干脆，行动的成本越低; 所以可简单认为信息价值和信息量成正比，即
v(xi, yj)＝uijI(xi; yj)
(5.10.1)
其中uij∈［0,∞］可谓yj提供的关于xi的单位信息平均价值。
对vij求平均就得到
(5.10.2)
上式和S. Guiasu提出的效用信息公式类似［7］。
和v(xi; yj)相比，uij应当随i,j变化不大，可以先验地确定。比如仅当y3发生时，不同决策导致的价值差异较大( 由于系统此时对不同控制较为敏感); 则可令，比如
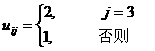
这样就可以粗略地由信息确定信息价值。
如果考虑单位信息价值和Y的熵有关，亦可采用
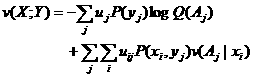
(5.10.3）
这一公式和热力学自由能增量公式类似，下一章说明。
有了上面式子，我们就可以用价值标准评价通信质量和优化通信; 比如评价天气预报质量和选择预报语句。
用给定的价值V＝v(X;Y)代替主观信息G求客观信息的极小值R得到的函数R(V)可谓保价值信息率函数，并且保质信息率R(G)可看作保价值信息率R(V)在uij＝1时的特例。当我们用价值标准衡量通信质量时，R(V)函数可为通信数据的压缩提供理论依据。R(V)函数有和R(G)函数同样的变化趋势，只是未必和直线R＝V相切。保价值信息率R(V)可以看作是给定P(X)和误差限制
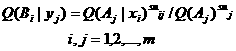
(5.10.4）
时的限误差信息率。
［1］张宏基编著．信源编码，人民邮电出版社，1987
［2］〔美〕Meditch J S． 随机最优线性估计与控制，赵希人译，黑龙江人民出版社，1984
［3］〔英〕Rosie A M． 信息与通信理论，钟义信等译，人民邮电出版社，1979
［4］Berger T．Rate distoration theory，Englewood Cliffs,N.J.:Prentice-Hall，1971
［5］周炯磐．信息理论基础，人民邮电出版社，1983
［6］鲁晨光．色觉的译码模型及其验证，光学学报，9,2 (1989)，158-163
［7］Guiasu S． Information Theory with Applications， McGraw-Hill，International Book Company，New York，1977
［8］鲁晨光, 汪培庄． 从“金鱼是鱼”谈语义信息及其价值，自然杂志，15，４ (1992),265-269