第四章 广义通信模型和广义信息测度
广义通信模型充分体现了这样的思想:信息来自预测,信息的多少需要事实检验; 越是把主观原以为偶然的事件预测为必然并且预测正确,信息就越多,否则信息就越少甚至为负值。根据这种思想,最一般的信息是预言信息,其他信息都是预言信息的特例。这一通信模型和K. R. Popper(波普尔)的科学进化模式[1]极为一致; 同时也贯彻和深化了马克思主义的实践检验真理思想; Weaver的一些思想[2]也由此得到贯彻[3-7]。
本章将要回答以下经典信息论无法回答的问题:
1) 当我们只知道过去的信源和信道而未来的信源和信道可能有所不同时,信息如何度量?
2) 当我们只能预测事实发生的条件概率——它是主观的,和事实可能相符,也可能不符时,信息如何度量?
3) 当我们只知道信号(比如语言)的意义或语义,而不知道事实发生的条件概率时,信息如何度量?
4.1 广义通信模型和Popper的科学进化论
关于知识或科学理论的进化模式,Popper认为,科学理论起于问题,为了解决问题人们提出假设,理论即假设; 假设受到事实检验;如果根据假设所作的预测与事实相符,就说它通过了检验并在某种程度上得到确证;如果与事实不符,它就被证伪了;于是人们又寻求新的更加经得起检验的假说或理论; 如此往复,以至科学进化。这种进化和生物进化是类似的。
关于科学理论和非科学理论的分界标准,Popper 认为:这就在于理论能否被证伪; 如果理论并不预言任何事件的发生有什么不同,则它就是逻辑上不可证伪的,因而也就是非科学的; 比如佛洛依德的精神分析理论不可证伪。
关于科学理论的进步标准,Popper认为[1]:
(1) 根据理论所作的预测和解释越是与事实或已有知识背景符合越好。
(2) 理论预期的结果越是出乎常识预料越好。
(3) 预言或命题的逻辑概率越小越好(比如“明天下大雨”和“明天下雨”相比,前者逻辑概率小,价值高,如果它们都和事实相符的话)。
(2)和(3)都意味着检验越严峻越好。
Popper实际上也就是用信息作为科学理论的分界和进步标准的,他说:
“凡是包含更大量的经验信息或内容的理论,也即在逻辑上更有力的理论,凡是具有更大的解释力和预测力的理论,从而可以通过把所预测的事实同观察加以比较而经得起更严格检验的理论,就更为可取。总之,我们宁取一种有趣、大胆、信息丰富的理论,而不取一种平庸的理论。”[1]
只是由于Shannon信息论无法处理广义信息,Popper 对科学理论的进步标准只能限于定性描述。
下面我们介绍和Popper科学理论进化模式相一致的广义通信模型[3],关于由这一模型得出的广义互信息公式怎样和Popper的科学进步标准相一致,本章最后一节介绍。
假设我们根据已知条件Z和知识K推出客观事件X 发生的概率或可能性分布QK(X|Z)(或写作Q(X|Z,K)),我们称QK (X|Z)为主观预测;这一预测通过语句Y间接表达出来。语言可能是自然的,也可能是人工的。再设事件集合A={ x1, x2,...,xm},语句集合B={y1,y2,...,yn},条件集合C={z1, z2,..., zl}; X,Y,Z分别是取值于A,B,C中元素的随机变量。要度量的是Z或Y提供关于X的信息。下面我们用P(X)表示X的概率分布,用P(xi)表示xi或X=xi的概率; 其他同理。
通信模型如图4.1.1所示:
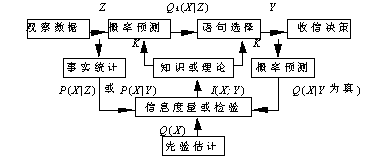
图4.1.1 广义通信模型
我们以数天内降水量预报为例说明该模型:Z表示气象数据,K为气象知识或理论;QK (X|Z)为气象台预测的各种降水量可能性分布(即概率预报,可用m×r阶矩阵表示)。Y是语句,比如“有小雨”,“有大雨”; Q(X|Y为真)是听众根据语义推出的降水量可能性分布。Q(X)是听众事先根据经验估计的降水量的可能性分布。
检验知识K的方法是看QK (X|Z)和Q(X|Z)哪一个更与P(X|Z)相符;若前者更加相符,K有正的价值,若后者更加相符,K有不如无。类似地,检验预报Y的方法是看Q(X|Y为真)和Q(X)哪一个更与P(X|Y)相符。气象台为了提供更多的信息,于是就一再改进理论或推理方法,试图作出更正确且更精确的预报。如此反复,使预报和事实趋于一致。
不光天气预报如此,疾病诊断如此,经济预测如此,各门科学知识的获得和进化也都如此。比如,古时侯,人们认为火来自燃素,燃素烧光了,火也就灭了。但是实践中人们发现这一理论与事实不符,比如有些液体燃烧后不是变轻了,而是变重了。后来拉瓦锡提出火的氧化反应理论,这一理论不仅能解释液体变重等现象,还能准确预测燃烧消耗和产生的不同物质的比重;这就提供了更多的信息,因而理论更为可取。
再比如,古时侯人们认为太阳绕地球转,但是这和观察事实不相符合;为此,哥白尼提出日心说,使预测的各行星轨道与事实较为吻合,于是提供更多信息;后来刻卜勒又把圆形轨道修改为椭圆轨道,使预测和观察吻合得更好…
当然,在地心说的基础上,假设各行星不仅绕地球转而且绕各自的本轮转,加了许多这样的本轮后也可能使理论和观察事实相吻合,但是从单位语句信息的角度看,它仍然不足取。后来的牛顿力学之所以更有意义,乃是因为它通过简单的力学公式准确地预言了极为普遍的物理事实,单位语句信息量极大。越具有普遍性的命题逻辑概率越小,后面说明,如果它是对的,则提供的信息越多。
由模型可见,最一般的信息是预言信息。下面是模型的几个特例。
1) 对于所有k,如果总有
QK (X|zk) = P(X|zk)
这表明预测和事实相符合,这时预言信息就变为描述事实的语义信息。
2) 如果没有语言表达环节,信息由Z而不是由Y提供,则预言信息就变为概率预测信息。
3) 如果既有1)又有2),并且Q(X)=P(X),则这时预言信息就变为Shannon信息。可以说 Shannon信息是客观信息,广义信息是主观信息,前者是后者在认识完全正确时的特例。
4) 当所有QK (xi|zk)∈{0,1},或Q(xi|Aj)∈{0,1}时,表示预测的是确定事件。不过确定事件只是不确定事件的理想极限;即使物理定律,由于测量的分辨率有限及噪声干扰,用以检验的数据和理论预测的物理量都是更小范围内的不确定事件;所以,对于看似确定的物理事件,模型同样适用。
4.2 信源和信道可变时的概率预测信息
为使从Shannon理论到新理论有一个平缓的过渡,我们看信源和信道可变时的信息量计算。这里,我们将依然保留经典信息论的核心——信息量等于后验概率和先验概率之比的对数。但是我们还要加上一条:信息的多少还取决于事实的检验。
假设信源信号是X∈A,信宿信号是Z∈C;信源和信道可变,过去的和未来的不一样;Q(X)和Q(Z|X) 表示由经验或过去统计(t时刻以前)得到的信源和信道;P(X)和P(Z|X)是我们暂且还不了解的未来实际发生的信源和信道。我们称Q(X|zk)为经验预测,它由下式确定:
Q(xi|zk)=Q(xi) Q(zk|xi)/ Q(zk)
(4.2.1)
称P(X|zk)为事实,Q(X)为先验估计或估计。
现在考虑t时刻以后的一小段时间内的信息传递。因为接收信息时,我们只知道Q(xi|zk)和Q(xi),而不知道P(xi|zk)和P(xi),未来的P(xi|zk)和P(xi)对当前的信息接收也不会有影响; 所以先验和后验概率只能用Q(xi)和Q(xi|zk)。推广经典信息量公式得
![]()
(4.2.2)
其中IF表示根据经验或过去统计预测得到的信息; P(xi|zk) 反映了事实检验。
上式中三个概率先后于T1, T2和T3时刻确定(T1< T2< T3),因而上式也可写作
![]()
(4.2.3)
其中Q(xi|T1)=Q(xi),其他类推。
如果用于检验的事实是确定的,即P(xi|zk)∈{0,1},则P(xi|zk)=1,这时(4.2.2)可简写为
![]()
当Q(xi|zk)大于Q(xi)时,信息量是正的,小于时信息量是负的,等于时信息量为0。这正说明了预测比原先估计进步信息就增加,反之就减少。
现在我们可以更加清楚看出为什么经典信息量公式无法度量单个事件——象单个的天气预报和天气之间的信息,原因是它要求后验概率一定和事实符合; 如果不符合,比如无雨天气相应“有雨”发生时,它就无能为力。
假设t 时刻以后的事件发生频率不被记忆或不被纳入经验知识,则上式对t时刻以后的一段时间信息传递皆合适,并且zk提供的关于X的平均信息量是
![]()
(4.2.5)
其中P(xi|zk)∈[0,1]。 上为即预测平均信息公式或预测Kullback公式,它和Theil提出的Kullback信息公式的改进形式[8,9]结构相同,但有更丰富的内涵。
定理4.2.1 给定Q(X)的情况下,当经验预测和事实完全相符,即
Q(X|zk)=P(X|zk)
(4.2.6)
时,信息量IF (X; zk)达到最大。
证明 因为
![]()
其中后一项和Q(xi|zk)无关,前一项在
Q(xi|zk)=P(xi|zk)
时达最大(它的负值达最小,根据定理(3.3.1)。故预测和事实相符时IF (X; zk)达最大。
证毕
当(4.2.6)成立时,预测平均信息公式退化为Kullback 公式。可见Kullback信息是预测平均信息在预测和事实总是符合时的特例。
预测平均信息可以通过图4.2.1得到直观理解。

图4.2.1 预测平均信息图解
事实P(X|zk)一定时,若预测Q(X|zk)较之先验估计Q(X)更近于事实,则信息量为正值,反之为负值;Q(X)一定时,预测越近于事实,信息量越大。
对于IF (X; zk)求平均就得到概率预测互信息公式
![]()
(4.2.7)
与Shannon互信息类似,这里有
IF (X;Z)=HF(X)-HF(X|Z)
=HF(Z)-HF(Z|X)
(4.2.8)
其中HF(X)为X的预测熵,
![]()
(4.2.9)
为X的预测条件熵; HF(Z)和HF(Z|X)同理。
类似地,当经验预测Q(X|Z)=P(X|Z)时,HF(X|Z)有最小值,再当Q(X)=P(X)时,这个最小值就变为Shannon条件熵。
到此,关于预测互信息IF (X;Z),我们有两个重要结论:
1. 信源不变时,经验预测Q(X|Z)越是和事实P(X|Z) 相符,IF (X;Z)越大;
2. 当预测准确,即Q(X|Z)=P(X|Z)时,先验估计Q(X) 与实际信源P(X)越是不同,IF (X;Z)越大;即越是能正确地把偶然预测为必然时,IF (X;Z)越大。
4.3 单个事件之间的广义信息量公式
我们仍以天气预测为例说明。
推广(4.2.2),我们得到: 当且仅当事实xi发生时,知识K提供关于xi的信息(量)是
![]()
(4.3.1)
后面我们用H,I表示广义熵和广义信息,而用HS和IS表示Shannon熵和Shannon信息。
给定知识K时,zk提供关于天气xi的信息是
![]()
(4.3.2)
zk和K共同提供的关于xi的信息是
![]()
![]()
(4.3.3)
同理可得
I(xi; zk,K)=I(xi; zk)+I(xi;K|zk)
语义信息是类似的,下面我们着重讨论。对于语言通信来说我们一般并不知道P(xi)和P(xi|yj),所能做的是根据经验和语义知道Q(xi)和Q(xi|yj为真)。因而我们要用语句的逻辑概率代替它的普通概率或选择概率。推广式(4.2.2)得到:当且仅当事实xi发生时,
![]()
(4.3.4)
由集合Bayes公式得
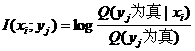

(4.3.5)
语义信息通常存在于两种场合。一种场合比如:老师教小孩说“25岁的人是青年人”;另一种场合比如:某人转告他人说“罪犯是青年人”。前一种场合传递的是理论知识,信息是I(yj; xi);后一种场合传递的是经验知识,信息是I (xi; yj)。因上式成立,两种场合下,语义信息的度量并没有什么不同。比如,可设yj为谓词“.是青年人”,对于前一种场合,让xi 表示25岁的人即可;而对后一种场合,让xi表示罪犯即可。
式(4.3.4)也可写为
![]()
(4.3.6)
意为:
语义信息量=语言所指事物的先验特殊性-后验特殊性
上面语义信息量公式将能保证:
1. 语句的先验逻辑概率Q(Aj)越小且后验逻辑概率Q(Aj|xi)越大,信息量越大,反之,信息越少,甚至是负值;
2. 语句越模糊,即Q(Aj|xi)和Q(Aj)越相近,信息量的绝对值越小。
下面举个例子检验式(4.3.5)。
例4.3.1 侦探根据犯罪现场推测罪犯(x)年龄,罪犯实际20岁;A是所有人的集合,其中有子集{20岁左右},{青年人} 等。下表是一些数据和计算结果。其中Q(Aj)和Q(Aj|xi)来自常识。
表4.3.1 语义信息量计算举例
|
Aj |
yj(x) |
Q(Aj) |
Q(Aj|x) |
语句评价 |
I(x; yj)(比特) |
|
{20岁左右} |
“罪犯20岁左右” |
0.2 |
1 |
精确 |
2.32 |
|
{青年人} |
“罪犯是青年人” |
0.3 |
1 |
较精确 |
1.73 |
|
{大人} |
“罪犯是大人” |
0.7 |
0.8 |
较模糊 |
0.19 |
|
{人} |
“罪犯是人” |
1 |
1 |
极模糊 |
0 |
|
{中年人} |
“罪犯是中年人” |
0.3 |
0.03 |
错了 |
-3.32 |

图4.3.1 罪犯年龄变化时同一预言的信息
显然,以上结果合乎常理。
当预言不变,为yj=“罪犯是青年人”时,罪犯年龄变化时,预言信息的变化如图4.3.1所示。
上面我们假定听者相信语句正确,如果不相信或不完全相信,则我们要用更加模糊的集合代替原来的集合。
类似地,我们可以推导出给定xi时,两个语句yj和yk之间的互信息公式
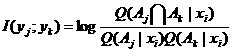
(4.3.7)
4.4 广义 Kullback公式及最佳预言选择
求Ik(xi; zk)的数学期望就得到K和zk提供的关于X的平均信息或理论预测平均
信息
![]()
它可以用于感觉和测量信号的信息度量。
例4.4.1 卖苹果的秤可能不准; X和Z是分别表示重量和秤的读数的随机变量; 设(对于买者)称重以前估计的重量的可能性分布是Q(X),根据读数zk的预测为QK (X|zk),而实际的重量分布为P(X|zk),则zk向买者提供的平均信息就如式(4.4.1)所求。
如果秤的读数总比实际重量大,而且买者相信它,信息就可能是负的。各种测量仪器和感官获得的平均信息是类似的。什么情况下平均信息量最多呢? 可以证明,P(X|zk) 的分布范围越小——意味着测量越精确,而且QK (X|zk)和P(X|zk) 越相同,则Ik (X; zk)越大。这是符合常理的。
对于预言信息,求I(xi; yj)的数学期望可得yj提供的关于X的平均信息量
![]()
![]()
(4.4.2)
这就是预言Kullback公式,我们也称之为广义Kull back公式。
预测平均信息公式是上式在Q(Aj)和Q(Aj|xi)归一化时的特例,有时我们也粗略地把(4.4.2),(4.4.1)和(4.2.5)统称为广义Kullback 公式。
当Q(X|Aj)=P(X|yj)时,I(X; yj)达最大; 再当Q(xi)=P(xi)时,上式就变成 Kullback信息公式。
天气预报常常碰到这样的问题: 在给定Z=z时,假设主观预测Q(X|z)与客观事实P(X|z)相符,那么选择怎样的语句最佳? 语句过于模糊则信息少; 过于清晰或精确,信息的绝对值可能大,但可能为负值,太冒险。利用下式
![]()
(4.4.3)
就可以求出预计的语句yj提供的平均信息量。注意语句的选择不影响事实的发生,因而总有P(xi|yj)=QK (xi|z)。 选择不同的语句,看用哪一个yj算出的平均信息量大,使平均信息量达最大的语句就最为可取。令
Q(xi|Aj)=QK (xi|z)
(4.4.4)
则可以求出可信度函数为
Q(Aj|xi)=Cj QK (z|xi)
(Cj为常数,Cj∈[0, max (QK (zk|xi)]
(4.4.5)
的语句提供的信息量最多。这也就是说,两条曲线Q(Aj|xi)和QK (z|xi)形状相似时,语句的信息量最多。
到此我们可以这样理解: 曲线QK (z|X)是信源的一个取值,曲线Q(Aj|X)是信宿的一个取值;经典通信中,信源和信宿的取值皆是确定的点,而对于广义通信,信源和信宿的取值可能是曲线; 两条曲线越相似,并且覆盖的范围越小,信息量就越多。
4.5 广义互信息公式及其性质
对Ik (X; zk)求数学期望就得到理论预测互信息公式; 对I(X; yj)求数学期望就得到预言互信息公式。我们统称它们为广义互信息公式。下面仅考虑后者。预言互信息公式为:
![]()
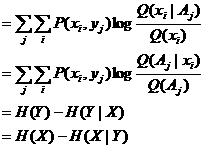
(4.5.1)
其中H(Y)是Y的广义熵,H(X)即X的预测熵HF(X);
![]()
(4.5.2)
![]()
(4.5.3)
两者分别是Y和X的模糊熵或广义条件熵。
当对于所有i,j,
Q(xi|Aj)=P(xi|yj)
(4.5.4)
时,我们称语句为真或模糊真。当语句模糊真时,H(X|Y) 就退化为Shannon条件熵; 再当Q(xi)=P(xi)时,I(X;Y) 就退化为Shannon互信息。
在信源不变,即Q(xi)= P(xi)的情况下,语句模糊真时,广义互信息有最大值,且等于Shannon互信息,这是易于理解的,因为信息从客观到主观的传递只减不增。
容易证明,当语句极为模糊,即Q(Aj|xi)=Q(Aj)时,
H(Y|X)=H(Y),I(X;Y)=0
当语义极为清晰,且语句使用正确,即对于所有i,j,当
Q(Aj|xi)∈{0,1},Q(xi|Aj)=P(xi|yj)
时,
H(Y|X)=0,I(X;Y)=H(Y)
当语义清晰但可能有错时,H(Y|X)和I(X;Y)分别为正、 负无穷大。因为实际上,我们对语言的怀疑总不能完全消除,因而绝对清晰的语义和无穷多信息损失只是理想极限,并不真的存在。
令P(xi)=1/m,i=1,2,...,m,B中只有两个互补语句,且语句使用正确,则
P(yj| xi)=Q(Aj|xi),H(Y|X) 就退化为 De Luca和Termini的模糊熵[10]。
虽然广义互信息是主观信息测度,但是它也有客观的编码意义(见第五章)。
广义互信息公式也可以用于感觉信息和测量信息的度量。设X∈A (A是连续的颜色集合),Z∈C={ z1, z2,..., zn}和Y∈B={y1,y2,...,yn}分别是表示原图象(象素)的颜色、量化后得到的数字图象(象素)的颜色以及人的颜色感觉的随机变量; yj是xj∈A的期望响应; 一种感觉yj可看作语句“和xj 相混淆的颜色出现”。于是用统计或集值统计方法可以得出xi和xj 相混淆的条件概率——它和隶属度一样记为Q(Aj|xi),其中Aj 表示和xj相混淆的颜色组成的模糊集合。再由统计得出P(Y|X)和P(X),然后用(4.5.1)就可以求出色觉的平均信息量。可以证明,人眼分辨率越高,数字图象的颜色看起来越和原图象的颜色相似,I(X;Y)就越大; 反之越小(详见5.8节)。
4.6 模式识别和天气预报信息评价
模式识别的任务是根据事物的特征判定事物属于若干个类别或模式中的一个。据遥感图象判别地表覆盖物是模式识别,根据病人症状作疾病诊断是模式识别,根据气象数据预报天气也是模式识别… 模式识别的一个重要问题是怎样评价识别的好坏。好的评价标准将有利于识别的改进。看来对于标准模式或类别模糊的场合,或模式并非互不相容场合,广义信息测度是更加客观且通用的评价标准。
设A={ x1,x2,...,xm}是事物集合,C={ z1, z2,..., zk }是各种特征集合,B={y1,y2,...,yn} 是要判断的类别或语句集合,比如yj (xi)=“xi∈Aj”(Aj被理解为第j种类别)。I(xi; yj)就是评价标准——根据xi的特征zk把xi判别为Aj。同理,I(X; yj)和I(X;Y)就分别是评价单个判别yj和所有判别Y的信息标准。下面以天气预报为例具体说明。
评价天气预报质量有许多不同方法[11,12],相比之下,信息论的方法较为合理;然而经典信息论不足之处之一是要求语义清晰,之二是不能度量某次天气预报提供的信息。广义信息测度可以弥补这些不足。
下一章要讲到,有些信息价值大,有些信息价值小; 如果考虑信息价值,除了信息标准,还有价值标准。这里只讨论信息标准。
有人以为天气预报的语言是清晰的,不存在模糊性; 他举例说,日降水量在10mm以下为小雨,在10-25mm之间为中雨,在25-50mm之间为大雨,在50mm以上为暴雨。
然而,上述降水量和“小雨”、“大雨”之间的关系说明了什么呢?只能说明在专业范围内,语言使用规则是清晰的( 而且是在已知确切的降水量的情况下),并不能说明语义是清晰的。举个例子说,现在预报第二天有大雨,而第二天的降水量是24或51mm,这算不算错报? 如果语义清晰,这就是错报。而实际上通常我们并不认为是错报。无论是从常识还是从广义信息论的角度看,报大雨都提供正的信息。
度量天气预报信息的语义信息量公式前面已经提供,下面我们举例说明具体计算。
例4.6.1 设A={ x0, x5, x10,..., x30}是可能的降水量集合(x5表示日降水量是5 mm,其他类推); 可选择语句集为B={y0 =“无雨”,y1=“有小雨”,y2=“有中雨”,y3=“有大雨”,...},xi在模糊集A1={有雨},A2={有小雨},A3={ 有中雨}和A4={有大雨}上的隶属度如表4.6.1所示。
求: 1) X=x10和X=x25时,哪一个语句提供的信息最多?
2) 已知概率预测如表第三行所示,假设预测正确,则选择哪一个语句信息最多,能否找到更好语句?
表4.6.1 先验概率分布、预测概率和语义
|
i |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
|
Q(xi) |
.8 |
.06 |
.03 |
.03 |
.03 |
.01 |
.01 |
|
QK (xi|z) |
0 |
.05 |
.1 |
.2 |
.35 |
.2 |
.1 |
|
Q(A1|xi) |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Q(A2|xi) |
0 |
.99 |
.9 |
.5 |
.1 |
.05 |
.01 |
|
Q(A3|xi) |
0 |
.01 |
.1 |
.4 |
.8 |
.5 |
.2 |
|
Q(A4|xi) |
0 |
.01 |
.01 |
.01 |
.1 |
.5 |
.8 |
1) 甲,乙,丙三人同时作了8次预报,第t次发生的天气是xt,如表4.6.2。问每人每次提供的平均信息是多少,哪个人提供的平均信息最多?
表4.6.2 预报记录
|
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
xt |
x0 |
x5 |
x5 |
x10 |
x15 |
x20 |
x25 |
x30 |
|
甲 |
y0 |
y1 |
y1 |
y1 |
y1 |
y1 |
y1 |
y1 |
|
乙 |
y0 |
y0 |
y2 |
y2 |
y3 |
y3 |
y4 |
y4 |
|
丙 |
y0 |
y2 |
y2 |
y4 |
y3 |
y3 |
y3 |
y4 |
4) 把Q(Aj|xi)理解为相似度,设 x5和x0之间的相似度Q(A0|x5)=Q(A1|x0)=0.1,则这时甲乙二人预报谁优?
解 1)
![]()
I(x15; y1)=log (1/0.2)=2.32(bit)
其他类推如表4.6.3。可见x15发生时,报“小雨”提供的信息最多,x25发生时报“大雨”提供的信息最多。
表4.6.3 各语句信息比较
|
|
y0 |
y1 |
y2 |
y3 |
y4 |
|
Q(Aj) |
.8 |
.2 |
.132 |
.0496 |
.021 |
|
x15 |
-∞ |
2.32 |
2.77 |
1.03 |
-∞ |
|
x25 |
-∞ |
2.32 |
-1.4 |
3.35 |
4.97 |
上面假设听众完全相信预报,如果不完全相信,Q(Aj|xi)=0和I(xi; yj)=-∞的情况都是不存在的; 这时应采用更加模糊的集合。
解 2) 由式(4.4.3)可得
I(X; y1)=log (1/0.2)=2.32(bit)
I(X; y2)=0log (1/0.2)+0.05log1+0.1log0.9
+0.2log0.5 +0.35log0.1
+0.2log0.05+0.1log0.01
=0.014(bit)
I(X; y3)=2.859(bit)
I(X; y4)=2.17(bit)
相比之下,当z发生时,y3提供的平均信息最多。
为求更好语句y',假设
P(X|z)=QK (X|z)=Q(X|A')
利用(4.4.5),取C'=0.05得Q(A'|xi)如下:
|
xi |
x5 |
x10 |
x15 |
x20 |
x25 |
x30 |
|
Q(A'|xi) |
.042 |
.083 |
.334 |
.44 |
1 |
.5 |
相应的平均信息是I(X;y')=3.045(bit)。
假设{ A2, A3, A4}是A的一个划分,则按B模糊集合代数,A3应当可由A1,A2和A4求出,即
Q(A3|xi)=Q(A1|xi)-Q(A2|xi)-Q(A4|xi)
表4.6.1中的数据便依据此假设。设A5=A3∪A4,A5可谓{中到大雨},并且
Q(A5|xi)=Q(A1|xi)-Q(A2|xi)
算得结果如下:
|
xi |
x5 |
x10 |
x15 |
x20 |
x25 |
x30 |
|
Q(A5|xi) |
.0 |
.1 |
.5 |
.9 |
.95 |
1 |
相应的平均信息是2.943比特,可见选择语句“中到大雨”近于理想。
解 3) 当预报次数很多时,使用(4.5.1)较方便; 而预报次数不是很多时,使用下式较为方便:
![]()
(4.6.1)
如此算得
I(X;Y,甲)=15.86(bit)
I(X;Y,乙)=-∞
I(X;Y,丙)=19.8(bit)
可见,丙提供的信息最多。因为甲的预报正确但不够精确,乙的预报精确但不够正确,丙的预报较为正确且精确。
解 4) 当Q(A0|x5)=Q(A1|x0)=0.1时,乙预报失真不再那么严重,I(X;Y,甲)不变,
I(X;Y,乙)=18.00(bit)
故乙比甲优。 解毕
由上例4)可见,将语义作模糊理解是避免严重信息损失的有效方法。实际上,我们大家就是如此理解日常天气预报的。评价天气预报也应采用这种宽容方法。
类似的方法也可以用来度量降水量地面分布预报的信息。
考虑语句y'=“最近R 地区有雨”提供的关于下雨的地面位置的信息。设X是地球上某处,有雨的先验概率地面分布为Q(X),后验概率是Q(X|A'),事实上下雨地区是S,概率分布是
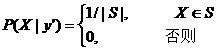
其中|S|是S的面积。考虑到实际下雨区域各处降水量不等,也可以假设P(X|y')是不均匀分布的。
于是y'提供关于下雨位置X的信息是
![]() dx
dx
![]() dx
dx
(4.6.2)
其中Q(A'|X)是X在模糊集合A'上的隶属度。
数学分析和上机计算结果都表明:
1. R和S重合越好,信息量越大;
2. R和S重合时,区域越小,信息量越大;
3. 越是偶然下雨的地方下雨被报准了; 信息量越大。
4.7 广义自信息 连续信源和信宿的广义互信息
设Q(X)=P(X),Q(X|Aj)=P(X|yj),则主观信息和客观信息相等,信息效率——设为两者之比最高。信息为
![]()
(4.7.1)
再令m=n,P(yj)=P(xj)(对于所有j),可得
![]()
=H'(X)-H'(X|X)=H'(X; X)
(4.7.2)
其中H'(X),H'(X|X)和H'(X; X)分别是X的广义熵,自模糊熵和广义自交互熵。
象X的Shannon自信息是I(X)=HS (X)一样,我们称I(X;X)=H'(X; X)是X的广义自信息。I(X;X)是一个看起来更加客观的信息测度,它反映了信源的变异度[13],也有其编码意义。
对于连续信源和信宿,广义互信息公式变为
![]() dxdy’
dxdy’
=H(Y)-H(Y|X)
(4.7.3)
其中
![]() dy’
dy’
![]() dxdy’
dxdy’
因为Q(A')和Q(A'|x)皆小于或等于1,H(Y)和H(Y|X) 皆为有限正值且有意义; H(Y)也总为正值。
4.8 自然语言通信的优点
到此可见,自然语言通信有三大优点:
1. 经典通信即经典信息理论讨论的通信中,收信者一定要知道信源和信道特性,即知道P(X)和P(Y|X); 然而,在日常通信,比如在语言和感觉通信中,收信者只需知道语言或信号的含义即可,无需知道信道的详细特性( 至多只需知道发信者是否有意撒谎); 这样就可以以不变应万变,避免了了解信源和信道特性要遇到的困难。
2. 在信源信号或客观事件不变的情况下,使用自然语言可以保证平均信息量较多(因为语言的模糊性)。
3. 可以根据具体情况对语言作灵活理解,减少失真造成的信息损失。
正是由于自然语言的上述优点,它将被越来越多地用于人工智能和专家系统中。
后面我们将看到,通信和控制系统中用均方差表示响应的失真,其实质也就是把信号意义模糊化; 和自然语言通信有类似之处。
4.9 由广义信息测度得出的科学理论进步标准
如果把信息量作为科学理论的进步标准,则我们可以得到如下结论:
1) H(X)一定时,Q(X|Y为真)和P(X|Y)越是相近,则H(X|Y)越小,平均信息量I(X;Y)越大;这也就是说,环境一定(从而Q(X)一定)时,理论解释或预测和事实越符合,则理论相对来说越进步。
2) 当H(X|Y)一定时,Q(X)和P(X)越是不同,或者说越是能把原以为偶然的东西预测为必然,H(X)和I(X;Y)就越大,知识或理论K就越进步。
3) Q(Aj)越小而Q(Aj|xi)越大(对于所有j),则I(X;Y)越大;这也就是说,命题或预言的先验逻辑概率越小,后验逻辑概率越大,相应的理论就越有价值;若两者总是相等,理论就是非科学的。
以上结论和Popper的科学进化理论基本一致。但也有一些分歧:
1) Popper 强调小概率命题的意义而否定大概率命题的价值;而由广义信息量公式得出的结论是: 命题的后验大概率也是必要的;Popper和Carnap的对立[1],可由广义信息量公式得到解决。
2) Popper忽视真假的模糊性,从而强调一个反例就足以证伪一个理论;而由广义信息测度公式得出的结论是: 虽然一个反例造成的信息损失远大于一个正例所带来的信息增加,但是由于分辨率和噪声的原因,一个反例带来的信息损失也总是有限的,因而它只能使理论在某种程度上变假。
有人批评Popper说,证伪一个命题和证实它的否定命题是等价的,Popper强调证伪贬低证实是不对的。
这是典型的误解。Popper说的是对同一个命题,多次证实也挡不住一次证伪。广义信息量公式完全支持这种看法。比如命题y'的先验逻辑概率是Q(A')=0.5,证实使后验逻辑概率为Q(A'|xi)=1; 证伪使后验逻辑概率为10-10,于是有
50比特=50log(1/0.5)
<|log(10-10/0.5)|
=|-70.3比特|
这就是说,命题在50次被证实的情况下提供的信息还不如在一次被证伪情况下减少的信息。
有人会说,你的信息理论和Popper的科学进化理论有怎样的预测和提供信息作用? 怎样被检验? 简单的回答是: 信息理论象数学一样是作为工具的科学; 首先,信息测度能精确反映知识的多少或某种编码极限,胜于常识估计,起到信道作用,因而能增加我们的信息量; 再者,它预测按某种方式行事,比如选择语句和信号,可以获得较大成功; 它的科学性可由它应用于通信和控制的有效性来检验。Popper理论类似。
第四章参考文献
[1]〔英〕波普尔,付季重等译. 猜想和反驳——科学知识的增长,上海译文出版社,1986
[2]〔美〕威弗尔. 通讯的数学理论的新发展,系统论控制论信息论经典文献选编,求实出版社,1989,612—636
[3]鲁晨光. 广义互信息公式和波普尔科学进化论的一致性,长沙大学学报7,2(2991),41—46
[4]鲁晨光.Shannon公式改造,通信学报, 12,2 (1991),95—96
[5]鲁晨光.B模糊集合代数和广义互信息公式,模糊系统和数学,5,1(1991),76—80
[6]鲁晨光.Shannon equations reform and applications, BUSEFAL 44,(Aut.,1990),45—52
[7]鲁晨光,汪培庄.从“金鱼是鱼”谈语义信息及其价值,自然杂志,15,4(1992),265—269
[8] Kullback S. Information and Statistics,John Wiley & Sons Inc.,New York,1959
[9] Theil H. Economics and Information Theory, North-Holland,Amsterdam,1967
[10] De Luca A. and Termini,S.: A definition of nonprobabilistic entropy in the setting of fuzzy sets,Infor. Contr. 20(1972),201—312
[11] 章基嘉.中长期天气预报基础,气象出版社,1985,421—435
[12] Cao H X(曹鸿兴). A Technique for verification of weather forecast and climate simulation with fuzzy sets,Advances in Atmospheric Sciences,4,3(1983),364—374
[13]〔英〕艾什比.控制论导论,科学出版社,1965,124