第三章 广义信息论基础

Shannon所涉及的数学概念上随机事件，客观概率，普通映射、等价观和集合划分；而广义信息理论所涉及的数学概念上随机集合、一般概略（客观概率、主观概率和逻辑概率）、广义映射、集合关系和集合覆盖。更广义的熵和信息测度建立在更一般的的数学基础之上，这是易于理解的。

本章关于集合、关系、映射、广义映射的介绍来子经典数学^[1]，关于各种概率以及模糊关系、模糊映射的介绍和已有的概率论^[2-7]及模糊数学理论大同小异^[8-10]，以集合和模糊集合为条件的，且反映三种概率之间关系的集合Bayes公式及各种广义熵（包括广义条件熵和广义交互熵）公式来自作者的研究，预测熵公式（3.3.1）和Aczel和Forte提出的广义熵公式(1.4.3)只差以负号。

读者最好把本章和第四章集合起来阅读，这样好加深理解。

3．1 集合Bayes公式 随机集落影

设信源信号集合(或字母表)A＝{x₁,x₂,...,x_m}，信宿信号集合B＝{y₁,y₂,...,y_n }，X和Y分别是取值于A和B中元素的随机变量。已知P(x_i)和P(y_j｜x_i)可以求出反条件概率

P(x_i｜y_j)＝P(x_i) P(y_j｜x_i)/ P(y_j)

 (3.1.1)

这就是Bayes公式，其中。

设A中子集A’，A’的特征函数为Q(A’｜X)∈{0,1},记X∈A’

的概率是Q(A’),则

（3.1.2）

我们记Q(x_i｜A’)＝P(X＝x_i｜X∈A’)，于是有

Q(x_i｜A’)＝P(X＝x_i, X∈A’)/P(X∈A’)

＝P(x_i) Q(A’｜x_i)/ Q(A’)

(3.1.3)

上式是以集合为条件的Bayes公式，我们简称它为集合Bayes公式，Q(x_i｜A’)便是A’中x_i发生的概率。

汪培庄提出的随机集落影理论把模糊集看作是清晰的随机集合的统计结果^[11]，据此，式(3.1.3)可被推广到集合模糊时的情况。

按随机集落影理论，x_i在A中的模糊子集A’ 上的隶属度被定义为

Q(A’|X)=P(X∈ζ’|X= x_i)=P(x_i∈ζ’)

(3.1.4)

其中ζ上响应A’的A上的随机集，于是

(3.1.5)

推广后的集合特征函数Q(A’｜x_i)又叫x_i在A’中的隶属度。

上式曾由Zedah提出^[13].

我们记Q(x_i | A’)=P(X= x_i |X∈ζ’)，于是有集合Bayes公式：

Q(x_i | A’)=P(X= x_i |X∈ζ)/P(X∈ζ)

     = P(x_i)P(x_i∈ζ)/P(X∈ζ)

   = P(x_i)Q(A’| x_i)/Q(A’)     

 (3.1.6)

对于不喜欢模糊数学的人，他可以直接把A’看作随机集，把Q(A’| x_i)看作x_i在随机集A’中的条件概率。我们使用模糊数学的语言是因为这样便于叙述和理解。

由第五、六章我们将看到，经典信息论已经不知不觉地用过式（3.1.6）;甚至统计物理学中也有类似公式。

3.2 客观概率 主观概率 逻辑概率

通常概率论所讨论的或Shannon信息论所涉及的概率是客观概率，或者说是基于频率解释的概率。要讨论主观预测和客观事实在多大程度上符合，这还要考虑主观概率和逻辑概

率。

我们以下雨为例说明三种概率的区别。假设所有天气分无雨，小雨和大雨三种。

    1) 由历年气象数据统计得到的某地某月某日无雨的概率为客观概率——即数理统计所使用的概率，后面有时也简称为概率,如P(x_i)，P(y_j| x_i)等即是。

    2) 预报员根据气象观察数据和理论（或听众根据预报语言）预测未来某天无雨的概率是主观概率——即Bayes学派所理解的概率^［3,4］，本书也称之为可能性测度或主观概率,后面的Q(x_i)，Q(x_i |A_j)等即是。

       3) 给定天气或日降水量时，某一语句比如“这天有大雨”被听众判断为真的概率是逻辑概率——即R. Carnap 等人所讨论的概率^{［5，６，7］}，它有时也被称之为置信度,后面的Q(A_j| x_i)，Q(A_j)等即是。

前面两种概率通常被视为概率的两种互不相容解释，自概率论诞生以来就有^［3］; 而在广义信息论中，这两者是互补的。

笔者认为模糊数学中的隶属度^[8]可以是命题的逻辑概率的不同解释。随机集落影理论^[11,12]使得使得隶属度来自随机集合的统计（见3.9节），这样，我们就把逻辑概率建立在随机集合的统计理论之上，从而扩展Shannon理论中所用的统计方法。

设事件(信源)集合A={x₁,x₂,…, x_m}，可选择语句和谓词集合B={y₁,y₂,…, y_n }; X和Y分别是取值于A和B中元素的随机变量，A_j是A上使y_j为真的事件构成的模糊子集，Q(A_j| x_i)使x_i在A_j上的隶属度，则命题y_j (x_i)的逻辑概率也就是谓词y_j的逻辑条件概率，为

Q(y_j (x_i)为真)＝Q(y_j为真| x_i)= Q(A_j| x_i)

(3.2.1)

类似地，谓词y_j的逻辑概率为

Q(y_j为真)＝Q(A_j)

 (3.2.2)

用求数学期望的方法得

(3.2.3)

实际生活中，我们往往不知道确切的客观概率P(X),而智能根据经验或过去的统计得到主观概率Q(X)(后面我们称Q(X)为经验信源)，则这时主观预测的y_j的逻辑概率为

（3.2.4）

后面若不说明则假定Q(X)=P(X)。

已知给定x_i时y_j被判定为真的概率是Q(A_j｜x_i)；现在求相反的问题：已知y_j或y_j (X)被判定为真，求各个x_i发生的条件概率Q(x_i | y_j为真)――主观概率或可能度，这一条件概率可由下面结合Bayes公式求出：

Q(x_i | y_j为真)= Q(x_i |A_j)

                    = Q(x_i) Q( (A_j| x_i)/ Q(A_j)

(3.2.5)

值得注意的是，语句y_j 同时具有客观概率即语句被选择的概率P(y_j)和逻辑概率Q(A_j)，两者一般不等;前者是纯客观测度，后者和主观理解的语义有关。比如某气象台一年到头总是报“无雨”，则选择概率P(“无雨”)＝1，而逻辑概率Q( “无雨”为真)则和“无雨”的语义有关，而和语句被选择与否无关;经验告诉我们，它约为0.8。

P(y_j｜x_i)和Q(A_j｜x_i)，Q(x_i｜A_j)和P(x_i｜y_j) 的区别同理。总之，两种概率或条件概率的区别是：

    1) P(y_j)和P(y_j｜x_i)反映语言使用规则；而Q(A_j)和Q(A_j｜xi)反映语义；前者因人而异，而后者大体上是由社会决定的。

    2) 选择概率是归一化的，而逻辑概率未必，一般有

原因是B中两个语句，比如“有雨”和“有大雨”，可能同时为真（由于蕴含关系,“有大雨”出现等价于两个语句同时出现）。后面说明，仅当{A₁, A₂,..., A_n}构成A的一个划分时，逻辑概率才是归一化的。

    3) 不仅逻辑概率而且逻辑概率密度的最大值为1； 而概率密度p(x)，p(y｜x)可能大于1。

虽然Q(x_i)，Q(x_i｜A_j)是主观概率，但是它们也是归一化的。

3．3 预测熵及其性质



  Shannon理论中假设信源不变，而现实通信中未必如此。

定义3.3.1 我们称

 (3.3.1)

为X的预测熵; 其中Q(X)是由过去的事实统计得到的X 的概率分布或根据经验知识预测的X的概率(主观概率)分布，P(X)是未来的一段时间内实际发生的X的概率或几率分布。

关于H_F(X)存在如下定理：

定理3.3.1 预测熵H_F(X)大于或等于Shannon熵H(X)，且Q(X)＝P(X)时，两者相等。

证明 由图3.3.1可知，存在下面不等式:

x-1≥lnx

(3.3.2)

设log 为2为底。因为

所以

H(X)≤H_F(X)

(3.3.3)

且仅当Q(X)= P(X)时两者相等。 　证毕

为了方便，后面我们有时简单地用H(X)表示H_F(X)。

3.4 映射 集合划分 Shannon熵

本书内容来自经典理论，为的是给下节内容作准备。

我们把直集上的一个子集R叫做A到B的一个关系；如果对于任一x_i，必有一个而且仅有一个y_j使得，我们就称R是从A到B的映射；这时通常是用f代替R，用y_j=f(x_i)代替；同时称y_j是x_i的象或函数，x_i是y_j的原象或逆象^[4]。显然，映射要求每个原象x_i必有一个且仅有一个象y_j，不过可能多个x_i有相同的象，有的y_j没有对应原象。

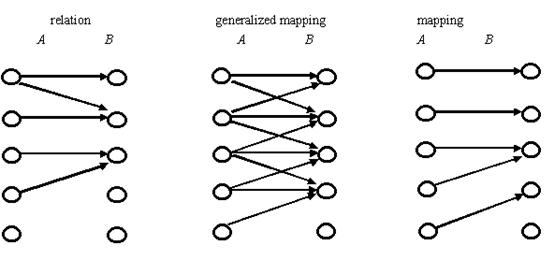
图3.41 关系，广义映射和映射比较

（书中没有，这里补充）

比如，A是所有人构成的集合，y_j=f(x_i)表示人x_i具有属性y_j (12个中的一种)，则f是映射。若y_j=f(x_i)表示x_i具有职业y_j或表示x_i会讲语言y_j，则f不是映射；因为有人没有职业，有人会讲不只一种语言。

A到B的关系可以用m行n列的0，1矩阵表示，第i行第j列的元素为1表示，为0相反。如果每行必有且仅有一个1，则所示该关系同时为映射。

例3.4.1 设A={10岁，20岁，30岁}， B={“是小孩”， “是大人”， “是老人”}由日常语义确定的A到B的关系

“是小孩”   “是大人”   “是老人”

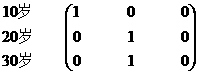
便是映射。

设A₁, A₂,…,An是A中子集，若

(空集)

(3.4.1)

则我们称A_j ={ A₁, A₂,…An}是A的一个划分。

设y_j的所有原象构成A_j，则{ A₁, A₂,…An}是A的一个划分。显然有

(3.4.2)

若y_j一定是A_j中x_i的响应，则P(y_j)= Q(A_j)，Shannon熵为

(3.4.3)

有集合划分，才有Shannon熵。比如度量天气集合的Shannon熵需要把所有天气强行为分无雨，小雨，大雨等若干个类别；度量一系列单色光的熵需要按波长把单色光分为许多小的波段。统计物理中有类似做法，一个相格就是一个划分单元。

若A_j不是A的一个划分，则(3.4.3)不成立。

3.5 广义映射 集合覆盖 广义熵

广义映射与映射不同的只是：每个x_i可能不止一个象。比如A是所有学生集合，B是各种语言集合， y_j=f(x_i)表示x_i会讲语言y_j，则f是广义映射。再比如A是所有人集合，B是语句集合{“是小孩”， “是青年”， “是成年” ”， “是老年” ”， “是大人”}，假设每个语句对每个人来说非真即假(后面谈及真假模糊时的情况)，则A到B存在的是广义映射。通常人们很少讨论广义映射，并认为A到B的广义映射可能化为A到B的幂集的普通映射来讨论。但是这里不便那样做。

设A₁, A₂,…An是A中子集，若

(3.5.1)

我们称{ A₁， A₂，…An}是A的一个覆盖。

设f是广义映射， y_j的原象构成集合A_j，则{ A₁， A₂，…An}是A的一个覆盖(证略)。

定义3.5.1 设A_j是广义映射中y_j所有原象构成的集合，我们称

(3.5.2)

是Y的广义熵(或语义熵，因为和y_j的语义或意义有关)。其中P(y_j)是y_j的选择概论，它是归一化的；而y_j的逻辑概论是Q(A_j)不是归一化的。

显然，如果Q(A_j)也是归一化的，则广义熵就变为预测熵；如果Q(A_j)= P(y_j)，广义熵就变为Shannon熵。

例3.5.1 设所有天气可分为x₁=无雨， x₂=小雨， x₃=大雨， A={ x₁， x₂， x₃}； P(x₁)= P(x₂)= P(x₃)=1/3； Q(X)= P(X)；有语句y₁=”无雨”， y₂=”小雨”， y₃=”大雨”， y₄=”有雨”， B={ y₁, y₂, y₃, y₄}；语句使用的条件概率和逻辑条件概率分别如下面两个矩阵表示:

y₁  y₂  y₃  y₄

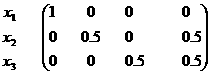
条件概率矩阵----反映语言使用规则

    y₁  y₂  y₃  y₄

逻辑条件概率矩阵----反映语义

左边矩阵第i行第j个元素代表的是P(y_j| x_i)；右边是成为广义映射的关系矩阵。于是有

P(y₁)= P(y₄)=1/3

P(y₂) = P(y₃)=1/6

Q(A₁)= Q(A₂) = Q(A₃)=1/3

Q(A₄)= Q(A₂) = Q(A₃)=2/3

                = (1/3)log3+(1/6)log3+ (1/6)log3+(1/3)log(3/2)

                   = 1.25(bit)   

这里的广义熵H(Y)也就是标志Y所指事物特殊性的熵。当语言不模糊且使用正确时，它就表示语句提供有平均信息量(第四章详述)。

例 3.5.2 均布于牛顿色盘边缘上的m种不同色调颜色构成集合A，m种色觉构成集合B，色觉y_j可能是x_j及与x_j相邻的两种颜色的象(由于人眼分辩率有限)，关系矩阵为

       y₁   y₂  y₃  y₄    …    y_n-1  y_n

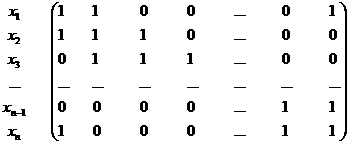
颜色和色觉都等概率，则Q(A_j)=3/m (j=1, 2, …m)色觉Y的广义熵为

  (bit)

在后面要说明它就是某种情况下色觉Y提供的平均信息量。

3.6 相似关系 相似度 不相似熵

在前面说的关系中，设B=A，若有

1) R是自反的，即对于所有I’( x_i, x_i)∈R；

2) R是对称的，即由(x_i, x_j) R可推出(x_j, x_i)∈R。

则我们称R是相似关系；

若同时有

3) R是传递的，即由(x_i, x_j)∈R和(x_j, x_i)∈R可推出(x_i, x_i)∈R

则称R是等价关系。

例3.6.1 集合A={爸爸(F)，妈妈(M)，儿子(S)上存在的相象关系是相似关系，同性别关系是等价关系，如下面矩阵所示:

    F     M    S

相似关系

    F     M    S

等价关系

注意，相似关系是不传递的。比如，由爸爸和儿子相似，儿子和妈妈相似，不能推出爸爸和妈妈相似。

A上的相似关系象广义映射一样，确定了A的一个覆盖；A上的等价关系象普通映射一样，确定了A的一个划分；反之亦然。

定义 3.6.1 令A_j是所有与x_j相似的x_i∈A构成的集合，我们称

(3.6.1)

为x_j和A中其它元素的平均相似度，其中r(x_i, x_j)∈{0，1}且仅当(x_i, x_j)∈R时r(x_i; x_j)=1.

前面我们把Q(A_j)称为y_j的逻辑概率，其实两者是相通的，后面阐述。

定义 3.6.2 设y_j的原象是A中所有与x_j相似的x_i，我们称A上相似关系确定的广义熵

(3.6.2)

是Y的不相似熵，称

(3.6.3)

是X的不相似熵——它是Y的广义熵在P(y_j)= P(x_j)时的特例，我们也称H’(X)为X或A的广义熵。

3.7 预测熵和广义熵的编码意义

我们先看预测熵H_F(X)的编码意义。

定理 3.7.1 设用一种编码规则对经验信源Q(X)作不失真编码，使得平均码长最短是L，近于

即L使得

(3.7.1)

其中为任意小的正值；则用这种编码规则对实际信源P(X)编码时，平均码长近于H_F(X)。

证明 设L_i是为x_i编码的码长，则平均码长为

比较上式和Shannon离散无记忆信源无失真编码定理，得

其中使得

则对信源P(X)编码时，平均码长为

它近于H_F(X)。 证毕

例3.7.1 设A={ x₁, x₂, x₃}，Q(x_i)，P(x_i)和编码如表3.7.1所示。

表3.7.1 可变信源编码

xi	Q(xi)	编码	P(xi)
x1	1/2	0	1/5
x2	1/4	10	2/5
x3	1/4	11	2/5

平均码长为

(bit）

而H_F(X)为

=1.8(bit)

我们再看广义熵的编码意义。

5.5节将证明，若把P(Y)看作信源(无记忆离散的)， P(X)= Q(X)看作信宿；若把y_j译码译为其源象集合A_j中任一元素时失真是允许的，则给定P(Y)时，

平均码长下限=广义熵H(Y)

下面仅举例说明编码方法。

例 3.7.2 A= B={0,1,2,…,9}，Y是信源，X是信宿，Y等概率发生，完全不失真传递信号所需平均长度为Shannon熵Hs(X)=log10=3.32比特；若仅要求|Y-X|≤1(算不失真)。试编码使平均码长近于广义熵H(Y)。

解 假设使平均码长达最短的P(X)也是等概率的。我们把信源序列分为三组，第0，3，6，9，…个分为一组，第1，4，7，10，…个分为一组，第2，5，8，11，…个分为一组；比如把548205740365…分为5273…，4046…和8505…，三组分别按表3.7.2所示规则编译码。

表3.7.2 平均码长近于广义熵H(Y)的编译方法

第一组	第二组	第三组`
信源 编码 信宿	信源 编码 信宿	信源 编码 信宿
0,1       00    0	0,1,2      00    1	0        00    0
2,3,4      01    3	3,4,5      01    4	1,2,3      01    2
5,6,7      10    6	6,7,8      10    7	4,5,6      10    5
8,9       11    9	9        11    9	7,8,9      11    8

可见平均码长为2bit。Q(A₀)=Q(A₉)=2/10，Q(A₁)= Q(A₂)=…= Q(A9)=3/10，广义熵为

H(Y)=–0.1(2log0.2+0.8log0. 3)

=0.23+1.39=1.62(bit)

和平均码长相近。因为P(X)的分布可以改进，并且对于每种编译码方法,00,01,10,11是不等概论的，因而还可以改进编码方法，使平均码长无限接近于H(Y)。由上例可以看出，X的不相似熵或广义熵H’(X)有类似的编码意义。

第五章对编码问题将作进一步讨论。

3.8 模糊映射 模糊相似关系 广义交互熵

在前面的关系矩阵中，如果元素r(x_i, y_j)∈[0，1]，则经典数学中的关系变为模糊关系。

定义 3.8.1 若模糊关系矩阵中的每一行元素之和

(3.8.1)

则我们称模糊关系为模糊映射(或模糊广义映射)；若上式等号成立，则称模糊关系为随机映射。

据此定义，条件概率矩阵表示的关系为随机映射，模糊数学中隶属度矩阵表示的关系为模糊映射。和流行的模糊映射定义不同的是，我们这里的模糊映射是由清晰到模糊的映射，而不是由模糊到模糊的映射。这里的模糊关系同理^[10]。

A上的模糊关系R可用元素为r(x_i， x_j)∈[0，1](i，j=1，2，…m)的m×m阶关系矩阵表示(下面有时把r(x_i, x_j)简写为r_ij)。

定义3.8.2 我们称直集A×A上的模糊子集R为A上的模糊相似关系，若

1) R是自反的，即r_ij=max(r_ij)；

2) R是对称的，即r_ij=r_ji；

3)

称R为模糊等价关系，若3)中等号成立(此定义也与已有定义^[10]有所不同)。

令A_j是与x_j相似的所有x_i构成的模糊集，则

Q(A_j | x_i)= Q( “x_i与x_j相似”为真)= r_ij

现在我们把相似度推广到模糊时的情况。

我们称r_ij为x_i和x_j的相似度；并且

(3.8.2)

为x_j的平均相似度(和已发生的所有X∈A相比)。

在B模糊集合代理数中^[15,16]，类似于经典数学中，称{ A₁, A₂,…,An}是A的模糊覆盖，若

称{ A₁, A₂,…,An }是A的模糊划分，若同时有

可以证明，模糊映射和模糊相似关系可分别确定A上的一个模糊覆盖；同样，随机映射和模糊等价关系分别可确定A上的一个模糊划分。反之亦然。

例3.8.1 人眼色觉分辩率可确定颜色集合A上的一个模糊相似关系，r(x_i, x_j)∈ [0,1]表示x_i, x_j相混淆的概率。这时例3.5.2中的相似关系矩阵变化大致也下：

       y₁   y₂  y₃  y₄    …    y_m-1  y_m

前面所述的广义熵H(Y)和不相似熵H (X)可以推广到映射或关系模糊时的情况，形式不变。此外，我们作如下定义：

定义3.8.2  称

(3.8.3)

为Y的模糊熵，后验广义熵或广义条件熵(它可蜕化为De Luca和Termini的模糊熵^[14])；称

 (3.8.4)

为X的模糊熵，后验预测熵或X的广义条件熵；称

(3.8.5)

为X的自模糊熵；称先验预测熵的后验预测熵之差(它等于先验广义熵和后验广义熵之差)

H(X;Y)= H (X)-H(X|Y)

= H(Y)- H(Y|X)

(3.8.6)

为广义交互熵，称

H’(X;X)= H’(X)- H’(X|X)

(3.8.7)

为广义自交互熵或自交互熵。

例3.8.2 有三种可能的降水量：x₁=0mm(毫米)，x₂=15mm， x₃=50mm， A={ x₁, x₂, x₃}； P(x₁)= P(x₂)= P(x₃)=1/3；有语句y₁=”无雨“，y₂=”小雨”， y₃=”大雨”， B={ y₁, y₂, y₃, y₄}；语句使用条件概率和逻辑条件概率分别如下面两个矩阵表示，求广义交互熵H(X;Y)。

y₁  y₂  y₃  y₄

条件概率矩阵——反映语言使用规则

y₁  y₂  y₃  y₄

逻辑条件概论矩阵——反映语义

解

P(y₁)= P(y₄)=1/3

P(y₂)= P(y₃)=0.5/3

Q(A₁)=1/3

Q(A₂)= Q(A₃)=1.2/3

Q(A₄)=2/3

(bit)

=0.46(bit) 

H(X;Y)= H(Y)-H(Y|X)=0.70(bit)

下一章将进一步讨论模糊熵和广义交互熵，并说明模糊熵正好反映语言或感觉的模糊性，广义交互熵正好成为广义信息测度。自模糊熵和自交互熵有类似意义。

3.9 隶属度确定 模糊分辩率函数

基于随机集落影理论，我们可用集值统计方法确定事件在某一模糊集比如{青年人}上的隶属度^[12]。具体方法是作多次确定清晰集合{青年人}的实验，每次确定的是随机集的一个取值，由此可统计出具有任一年龄的人在{青年人}上的隶属度。

在作者提出的B模糊集合代数中，模糊集分原子集和非原子集，适当选择原子集可使任一模糊集的隶属函数由一些原子模糊集的隶属函数算出^[15，16](见附录论文1)，从而简化统计。

作者这里提出确定隶属度的另一种方法，即假定：过去的y_j发生和X∈A_j等价，也就是

Q(x_i | A_j)= Q(x_i |y_j)，(对于所有i，j；后面不赘述)

(3.9.1)

由Bayes公式得

Q(A_j| x_i)/ Q(A_j)= Q(y_j| x_i)/ Q(y_j)

即

Q(A_j | x_i)=K _jQ(y_j|x_j)

(3.9.3)

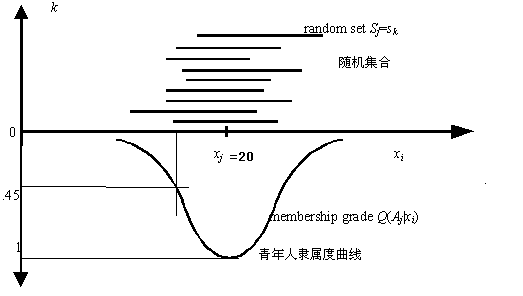
图3.9.1 由集值统计方法求得不同年龄的人在模糊集A’={青年人}上的隶属度

再假设Q(A_j | x_i)(i=1，2，…，m)的最大值是1，Q(y_j| x_i)的最大值是Q_max(y_j| x_i)，于是得

Q(A_j | x_i)= Q(y_j| x_i)/ Q_max (y_j| x_i)

(3.9.4)

在建立专家系统时，我们往往要由Q (y_j| x_i)的最大值为1假设求Q(A_j | x_i)。

例3.9.1 医疗专家把若干病人诊断为乙型肝炎病人，设y’=“乙肝”，X是病状数据；已有Q(X)、Q(y’)、Q(X| y’)，则一种症状x_i在模糊集A’={乙型病人}上的隶属度是

Q(A’| x_i)= Q(y’| x_i)/ Q_max (y’| x_i)

其中

Q(y’| x_i)= Q(y’) Q(x_i | y’)/ Q(x_i)

在上例中，如果以往病例不太充分，则Q(A’| x_i)无解，在这种情况下，可用插值方法解决。

后面我们把由感官分辩率确定的A上的相似关系矩阵中的一列，记作r(X; x_i)，叫做x_i分辩率函数；以上两种方法对于分辩率函数的确定同样适用。

为了理论分析方便，我们用钟形函数(几何曲线如图3.9.2所示)

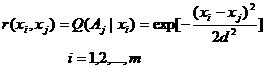
(3.9.5)

模拟真实的分辩率函数，其中d是反映分辩率高低的参数，d越小，波型越窄，分辩率越高。对于均匀的分辩空间，比如颜色光学中的匀色空间^[17]，d为常数，否则，d随j变化。

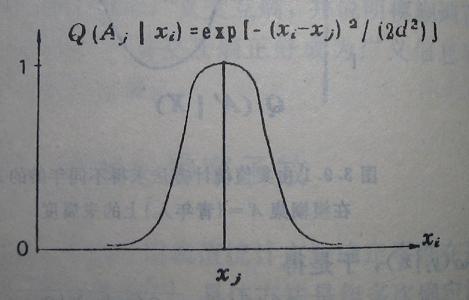
图3.9.2 钟型模糊分辩率函数

为了有效接收信息，往往感官能分辩的东西而大脑有意识地忽略它们的差别；比如电视图象上的雪花点很严重时，人脑便自动忽略细节，以便更好获得信息。我们称大脑分辩率为主观分辩率，它低于或等于感官分辩率。5.8节将讲到为什么有时降低感官或主观分辩率，比如远看屏幕，反而效果更好。

控制系统中，系统对控制信息响应的灵敏度也可用类似曲线表示。

3.10 隶属度的柏拉图解释

对于每个语句y_j，我们可以假设存在一个x_j (x_j可能不属于A)

使得

Q(y_j (x_j)为真)= Q(A_j |x_j)=1

(3.10.1)

从而可以把语句的逻辑概率Q(A_j | x_i)解释为x_i和x_j的相似度。这使我们想到柏拉图的理念哲学。

拍拉图认为^[18]，桌子有桌子的理念(idea)，马有马有理念；日常事物只是理念的影子，它们只是和理念相似，而不完全相同。上面假设的x_j就相当于y_j表达的理念，隶属度或命题的可信度Q(A_j|x_i)就相当于事物x_i和理念x_j的相似度。不同的是，这里x_j可能真地存在或属于A。

当然，我们也可以不说理念而说典型。从具体事物和典型相似的角度来看模糊集合和隶属度可以加深我们对模糊数学的理解。可以说模糊数学的生命力就在于它考虑到不同事物之间的相似性。

同时我们也看到，一种感觉或一个仪器测量值y_j就相当于一个语句“X∈A”。语义信息和感觉或测量信息在本质上相同。

参考文献

［1］张禾瑞.  近世代数基础，人民教育出版社，1978，1-30

［2］江天骥.  归纳逻辑导论，湖南人民出版社，1987，180-183

［3］陈克艰. 上帝怎样掷骰子，四川人民出版社，1987，119-28

［4］王雨田. 概率逻辑，王雨田主编，现代逻辑科学导引，中国人民大学出版社，1988，1-42

［5］Carnap R. 归纳逻辑与演绎逻辑，洪谦主编，逻辑经验主义，商务印书馆，1982

［6］Reichenbach H．概率概念的逻辑基础,洪谦主编逻辑经验主义，商务印书馆，1982

［7］〔英〕波普尔，付季重等译．猜想和反驳——科学知识的增长，上海译文出版社，1986

［8］Zadeh L A. Fuzzy sets，Infor. Contr. 8 (1965)，338—353

［9］汪培庄.  模糊集合论及其应用，北京师范大学出版社，上海科学技术出版社,1983

［10］葛苏林. 模糊子集　模糊关系　模糊映射，北京师范大学出版社，1985

［11］汪培庄. 模糊集和随机集落影，北京师范大学出版社，1984

［12］张南纶. 随机现象的从属特性与概率特性，武汉建材学院学报， 1,2(1981).

［13］Zadeh L A. Probability measures of fuzzy events，Journa of　Mathematical Analysis and Applications 23(1968)，421—427

［14］De Luca A. and Termini S. A definition of nonprobabilistic　entropy in the setting of fuzzy sets，Infor. Contr. 20(1972)，201—312

［15］Lu C G. Fuzzy switching quasi－Boolean algebra and vision simulation colour discernment，BUSEFAL 36(1988),132—138

［16］鲁晨光. B模糊集合代数及其用于语义信息和颜色视觉，北京师范大学学报，27,增2(1991),30—36

［17］鲁晨光. 色觉的译码模型及其验证，光学学报，9，2(1989)，158—163