第二章 Shannon信息论述评
Shannon信息论建立在随机事件统计理论的基础上[1]。为此,我们先简述基于频率论解释的概率理论,下一章再阐述更广意义的概率理论[2]。这里Shannon信息论只是取其要义,我们尽可能使用浅显易懂的方式叙述,以照顾不熟悉Shannon 理论的读者。本章还含有对经典信息理论的评论,熟悉Shannon 理论的读者也不妨选看。
2.1 基于频率解释的概率论
概率论诞生于赌博问题,这里我们也且用掷骰子为例来说明什么是概率。
一个骰子可能呈现的数字是1,2,3,4,5,6中的一个。一般情况下,每个数字出现的几率大致相等;比如你掷N=600下,1出现的次数N1大约为100下。设为110下,则110/600叫做1 出现的几率(或数学几率)。当掷的次数无穷多时,这个几率就无穷地接近1/6,1/6就是1出现的概率,即
P(X=1)=1/6
其中X表示随机变量,对于本例它的取值范围是集合A={1,2,3,4,5,6},即X∈A。设一般情况下,A={x1, x2,..., xm},按频率论解释,概率P(X=xi)被定义为:实验次数N为无穷大时,X=xi的次数Ni和N之比的极限; 即
![]()
(2.1.1)
按照现代概率论,只要某种测度符合概率的公理化定义,它就构成概率测度。这一公理化定义是:
设Ω是一集合,它的一些子集构成Borel域β,存在一个映射P:β→[0,1],它满足条件
(1) P(Ω)=1;
(2) 对于任一Ai∈β,有0 ≤P(Ai)≤1;
(3) 若Ai和Aj互不相交,
![]()
则称P为β上的概率测度。
其中(3)被称为概率的可加性要求。按照这一定义,除了基于频率论解释的概率,还存在其他类型的概率(见第三章)。
下面我们简单地用P(xi)表示P(X=xi)。
对于掷骰子,因为下式
P(1)=P(2)=...=P(6)=1/6
成立,所以我们称X是等概率事件。如果骰子中放了铅,重心不在骰子中心,则上式将不再成立,各数字将不再是等概率事件。但是无论如何,总有
![]()
(2.1.2)
上式又叫归一化条件。
再设Y∈B={ y1, y2,..., yn}。我们称
P(xi, yj)=P(X=xi,Y=yj)
为xi和yj的联合概率。根据定义有
![]()
(2.1.3)
![]()
(2.1.4)
我们定义
P(xi| yj)=P(xi, yj)/ P(yj)
(2.1.5)
是给定条件yj时xi|的条件概率; 同理,条件概率
P(yj| xi)=P(xi, yj)/ P(xi)
(2.1.6)
由(2.1.5)和(2.1.6)得
P(xi| yj)=P(xi)P(yj|xi)/ P(yj)
(2.1.7)
这就是著名的Bayes公式。
若P(yj |xi)=P(yj),则意味着Y=yj和X=xi无关,这时
P(xi, yj)=P(xi) P(yj)
以上各种概率都是归一化的。当A,B为连续事件,比如为[0,1](实数区间)时,P(xi)和P(yj)就变为p(x)和p(y)(大写P变为小写p),p(x)和p(y)不再表示概率,而是表示概率密度。p(x,y)等同理。这时有
![]() dx
dx
(2.1.8)
其他类推。
2.2 经典通信模型
Shannon信息论中的通信模型如图2.2.1所示。如果把编译

图2.2.1 Shannon通信模型
码部分并入信道,则该模型如图2.2.2所示。我们且讨论信源离散时的情况。这时图2.2.2 可以具体地变为图2.2.3。
图2.2.3中从xi到yj的箭头表示X=xi时Y=yj发生的条件概率是P(yj|xi)。我们用P(Y|X)表示m行n列的条件概率矩阵,因为它是物理信道的抽象,信息论中也称之为信道。
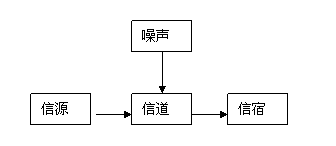
图2.2.2 简化的Shannon通信模型

图2.2.3 有噪声通信模型
2.3 经典信息量公式和Kullback信息公式
为了便于讨论,我们从单个事件之间的信息量公式出发,然后推导出Shannon互信息公式和Shannon熵公式。
经典理论中,信息量是对减少的不确定性的度量。它的数学表示通常被写为:
![]()
(2.3.1)
其中I(xi, yj)是yj提供的关于xi的信息量; P(xi)是xi的先验
概率,P(xi|yj)是xi的后验概率(给定yj时)。log 表示对数,可以是自然对数(以e为底),这时信息量单位是nat; 也可以是以2为底,这时信息量的单位是bit或比特。信息论中一般用bit。
注意:上式所求信息是一系列X和Y发生后,回过头来看yj提供关于xi的信息,而不是某一次yj提供的关于xi的信息。因为如果某次xi不相应yj出现时,就不会有这样的信息。这就是为什么Shannon 奠基性论文中没有该公式而且也不谈单个信号的信息。后面我们将看到,仅当我们考虑预测和检验,并且xi确实相应预测yj发生时,上式才能用于单个信号——比如语句“明天有雨”或电压表读数“230伏”——的信息的度量。而经典信息论不考虑预测信息。
上式也可以写成
![]()
(2.3.2)
等式右边两项分别表示先验不确定性和后验不确定性。若后验不确定性为0,则公式变为
![]()
(2.3.3)
据Bayes公式可得
![]()
![]()
![]()
(2.3.4)
这表明两个事件相互提供的信息量必然相等。若两事件相互无关,则P(xi|yj)=P(xi)且P(yj|xi)=P(yj),I(xi; yj)=0。这显然合理。
值得注意的是,I(xi; yj)也可能是负的。下面举个例子看经典信息量的计算。
例2.3.1 假设A,B是互不相容事件集合;X ∈A={x1=抽烟多的人,x2=抽烟少的人};Y∈B={ y1=有肺病,y2=无肺病};P(x1)=0.3,P(y1)=0.2,P(x1, y1)=0.12; 求I(x1; y1)和I(x2; y1)。
解
P(x1| y1)=0.12/0.2=0.6
I(x1; y1)=log(0.6/0.3)=1 bit
P(x2| y1)=1- P(x1| y1)=0.4
P(x2)=1- P(x1)=0.7
I(x2; y1)=log(0.4/0.7)=-0.81 bit 解毕
求I(xi; yj)的数学期望就得到yj提供的关于xi的平均信息量:
![]()
![]()
(2.3.5)
上式和Kullbak信息公式类似,但是有更丰富的内涵。我们且也称之为Kullback公式。后面将说明,如果把P(X|yj)
理解为预测的可能性测度,则I(X; yj) 就是预测和事实一致时的平均信息。可以证明I(X; yj)必然大于0,它不等于X的熵的减量
H(X)-H(X|yj)
该减量可能为负值。
例2.3.2 在上例的基础上,求y1提供的关于X 的平均信息量。
解
I(X; y1)=0.6×1+0.4×(-0.81)=0.28 bit
2.4 Shannon互信息公式
同样,求I(X; yj)的数学期望,我们得到X和Y 之间的平均信息量
![]()
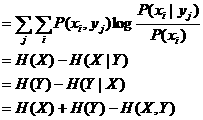
(2.4.1)
这就是著名的Shannon互信息公式;其中H(X)和H(Y)分别是X和Y的熵;H(X|Y)和H(Y|X)分别是X和Y的条件熵; H(X,Y)是X和Y的联合熵。并且
![]()
(2.4.2)
![]()
(2.4.3)
![]()
(2.4.4)
H(Y),H(Y|X)可以类推。这几种熵之间存在的关系是
H(X)+H(Y|X)=H(X,Y)=H(Y)+H(X|Y)
(2.4.5)
可以证明,上述诸熵皆大于或等于0。
当P(yj| xi)∈{0,1}(对于所有i,j)或P(Y|X)∈{0,1} 时,表示信道无噪声,这时H(Y|X)=0,I(X;Y)=H(Y)。当P(yj| xi)=P(yj)时,表明噪声极大,这时H(Y|X)=H(Y),I(X;Y)=0。
若Y=X,则H(Y|X)=H(X|X)=0,I(X;X)=H(X)。I(X;X)叫做X的自信息,因为它在数值上与H(X)相等,所以人们有时也称H(X)为自信息。但需注意,当我们说H(X)是X 的平均信息量时,我们实际上指的是I(X;X)。
2.5 连续信源的熵和交互熵
有人说,连续信源的Shannon熵存在先天不足[4]。在经典理论中,求连续信源熵的权宜方法是把连续信源离散化,然后用离散信源的Shannon熵度量。
设A=[a,b],我们把[a,b]分成m等份,每个等份的宽度是△=(b-a)/m。再设第i个区间的概率密度不变,为p(xi),则P(xi)=p(xi)△,
![]()
![]()
![]()
(2.5.1)
令m→+∞,则△→0,得到X的Shannon熵
![]()
![]()
![]()
(2.5.2)
上式中,第二项为无穷大;第一项为Hr(X),Hr(X)被称之为相对熵,它一般为有限值,但可能为负值。比如
b-a<1 且 p(x)=1/( b-a)
时,有p(x)>1,从而有
![]()
当信源和信宿皆连续时,互信息仍然存在,为
![]()
![]() dxdy
dxdy
(2.5.3)
其中p(x,y)为联合概率密度,p(y|x)是条件概率密度。Hr(Y)和Hr(Y|X)可从Hr(X)类推。
对于连续信源,虽然I(X;Y)仍有意义,但是Hr(Y)和Hr(Y|X)等皆无实际意义且可能为负值。
2.6 信道容量和信道编码
Shannon 定义了两个重要函数:信道容量和保真度信息率[1,5]。关于后者的理论后来又有所发展,并且保真度信息率被改称为信息率失真(information rate-distortion)[6]。信道容量和信息率失真分别是通信的数量和质量指标。如果把通信系统和生产系统相类比,则信道容量就相当于生产能力,而信息率失真就相当于给定产品质量要求时,单位产品所需要的最少劳动量。
首先我们介绍信道容量。
给定信道P(Y|X),信源H(X)不同,互信息I(X;Y)也不同。
信道容量被定义为:给定信道P(Y|X)时,改变信源P(X) 使得互信息I(X;Y)达最大,这个最大值就是信道容量。设PC 是所有可能的信源构成的集合,则信道容量C的数学定义是
![]()
(2.6.1)
信道容量告诉我们不要期望用有限容量的信道传递过量的信息。求信道容量的具体方法在经典信息论中有详细讨论; 下面我们只简要介绍一下连续高斯信道——即有正态分布叠加噪声的信道——的容量。
设X∈A=B=(-∞,+∞),叠加性噪声Z是均值为0,方差(或功率)为![]() 的高斯变量,则输出为Y=X+Z ,并且
的高斯变量,则输出为Y=X+Z ,并且
![]()
(2.6.2)
![]()
![]()
(2.6.3)
可以证明,在输出功率Pwo的限制下,Hr(Y)在Y为正态分布时有最大值;这时I(X;Y)也有最大值:
![]()
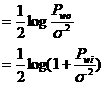
(2.6.4)
其中Pwi是输入功率。上式表示,和输入功率相比,噪声功率越小,信道容量越大。
Shannon信道编码定理告诉我们,给定信道时,只要传递的信息小于C,我们总可以通过在原信源和信道之间加一个编码环节作某种编码,使得在信道输出端无失真地译出信源信号的概率无穷地接近于1。编码的目的实际上就是使信源和信道相匹配。
2.7 Shannon熵的编码意义
使用电报通信的早期,人们用长短不同的信号表示所要传递的字母A,B,C,...。设长短信号分别用0,1表示,则一个字母可用一个0-1码,比如001表示。后来发现,用较短的0-1 码表示经常出现的字母,比如E,而用较长的0-1码表示较少出现的字母,比如X,这样就能在传递相同电文的情况下所用0-1码的总长度最短,或每个字母所用平均码长最短。然而,要想不失真地,即在H(X|Y)=0的情况下,传递电报电文,平均码长最多能缩短到多少呢?Shannon理论告诉我们,这个平均码长的极限就是H(X)(即H(X)的bit数)。
本节和下一节都假设信源信号前后无关或信源是无记忆的。
下面我们用一个例子来说明H(X)的编码意义。它来自文献[7]。
例2.7.1 假定信源可以输出8个独立的消息:
A,B,C,D,E,F,G,H;它们出现的概率、各种编码以及相应的平均码长c如表2.7.1所示。
表2.7.1 几种编码的平均码长c
|
xi A B C D E F G H |
|
P(i) 0.1 0.18 0.4 0.05 0.06 0.1 0.07 0.04 H(X)=2.55 |
|
等长码 000 001 011 010 110 111 101 100 c=3.00 |
|
Fano码 100 01 00 1110 1101 101 1100 1111 c=2.64 |
|
Haffman码 011 001 1 00010 0101 0000 0100 00011 c=2.61 |
表中结果显示,采用适当的编码方法可使平均码长c接近H(X)。如果把相继的几个字母当作一个字来编码,平均码长会无限地接近H(X)。可见Shannon熵有其客观性。
2.8 限失真编码和信息率失真论
保真度信息率之所以被改称为信息率失真,主要是因为Shannon的“保真度”是用失真度来定义的。在广义信息论中,通信质量被认为是由主观信息量的相对多少来确定的,不仅和失真,也和逼真(或信号的意义)有关,我们将用“保质(量)信息率”一词取而代之。
我们先看限失真编码问题。
设信源发出xi时,信道输出yj; 则yj可能在不同程度上失真。我们用dij∈(0,+∞)表示yj相对于xi的失真量,则Y 相对于X的平均失真量为
![]()
(2.8.1)
dij是怎么来的?在经典信息论中,它是主观人为定义的。当xi和yj皆是数字时,常用的定义是[7]
dij=f(|yj-xi|)
(2.8.2)
f是只增不减函数。比如
dij=(yj-xi) 2
下面举例说明降低失真要求可以大大缩短平均码长。
例2.8.1 设有二元信源,A=B={0,1},P(x1)=P(x2)=1/2,
![]()
我们把信源信号四个分为一组,编译码如表2.8.1所示。
表2.8.1 有失真编码
|
组号 |
信源信号 |
编码 |
译码 |
|
1 |
0001 0000 0011 1001 |
00 |
0001 |
|
2 |
1010 1011 0010 1110 |
01 |
1010 |
|
3 |
0111 0110 0101 1111 |
10 |
0111 |
|
4 |
1100 1101 1000 0100 |
11 |
1100 |
第一行是说0001和0000等四组码同样用00编码,译码同样得0001; 其他类推。较之无失真编码,如此编码使平均失真量由0 升到(3/16)a=0.188a,而平均码长则降低到2/4=0.5。
现在问:给定信源和限失真D,平均码长最短能达多少?
Shannon离散无记忆信源限失真编码定理告诉我们,这一极限就是保真度信息率或信息率失真。
设D是所要求的平均失真上限,PD是所有使d(X,Y)≤D的信道的集合,则信息率失真被定义为
![]()
(2.8.3)
之所以说信息率而不说信息是因为I(X;Y)在这里表示的是单位符号传递的信息。
求R(D)函数的一般方法是在一些限制条件下,利用拉氏(Largrange)乘子法,改变P(Y|X) (反映编译码方法改变),求I(X;Y)的极小值。下面即是。
已知
![]()
(2.8.4)
![]()
(2.8.5)
![]()
(2.8.6)
其中
![]()
令P(yj| xi)的泛函
![]()
(2.8.7)
再令F对所有P(yj| xi)的偏导数为0,得
![]()
令logλi=μi/P(xi),得
![]()
(2.8.8)
由上式和(2.8.6)得

(2.8.9)
最后得R(D)函数的参量表示:
![]()
(2.8.10a)
![]()

(2.8.10b)
可以证明dR/dD=s。s是函数R(D)的斜率,它的物理意义是增加单位失真量时信息率R的增量。因为R随D减小而增大,所以s为负值。
对于连续信源有类似结论。
现以二元信源为例说明失真函数dij对称情况下R(D) 函数的计算及其性质; 5.6节还将讨论它在广义信息论中的形式。
设二元信源和失真如例2.8.1,最后推导出
![]()
(2.8.11a)
![]()
(2.8.11b)
R(D)函数如图2.8.1所示。图中假设P(x1)=P(x2),H(X)=1bit 。图示实线表明,要想减小D,必须增大R;当D=0时,R =1 bit ,表示无失真地传递信号需要1 bit的互信息。
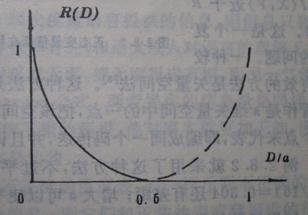
图2.8.1 二元信源失真对称时的R(D)函数
其中虚线部分是按式(2.8.1)画出来的,由于经典理论不考虑谎言信息或负信息,所以虚线部分不好理解,经典信息论中对此也避而不谈。看过本书后面保质信息率的讨论可以理解。
例2.8.3 设有连续信源和信宿A=B=(-∞,+∞),信源呈正态分布,失真函数为方差,即d(x,y)=(y-x)2时,s(D)和R(D)函数为(详见[5]):
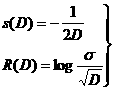
(2.8.12)
图2.8.2显示了,当D近于0时,R(D)为无穷大。这说明对于连续信源,失真不可避免。当D=![]() 时,R(D)=0;这表示,若允许失真等于y和x的方差,无须信息传递,不管X取何值,输出Y一律等于X的均值即可。
时,R(D)=0;这表示,若允许失真等于y和x的方差,无须信息传递,不管X取何值,输出Y一律等于X的均值即可。
图2.8.2 正态变量信源在均方误差准则下的R(D)函数
率失真函数告诉我们在D的限制下,信号单位符号最少需要传递多少信息;然而它并没有告诉我们怎样对信源编码才能真地在D的限制下,使I(X;Y)近于R(D)。这是一个复杂问题。一种较为有效的方法是矢量空间法[8]。这种方法是,把一组n个信源信号看作是n维矢量空间中的一点,把该空间化成若干块,每一块用一个点来代表,即编成同一个码传送,并且译码译成同样的n个信号。例2.8.2就采用了这种方法,不过平均码长0.5和极限值R(3/16)=0.304还有差距; 增大n可以使平均码长更短。
R(D)函数的反函数D(R)为给定信息率R时,失真d(X,Y) 的最小值,也有其优化通信意义。
如果dij不是yj相应xi时产生的失真量,而是价值损失,则D就表示价值损失限制,R(D) 就表示限价值损失时的最小信息率[5]。
2.9 Shannon信息论的局限性
Shannon或经典信息论局限性具体表现在:不便于度量语义信息、感觉信息、信源信道可变时的信息以及单个信号的信息。作为数据压缩理论依据的率失真理论也远不完善。究其原因,乃是因为它只考虑信号传递,而不考虑信号的意义或观察者对信号意义的理解;或者说,它只考虑客观信息,而不考虑主观信息。由于不考虑意义问题,它也就不会考虑意义的模糊性或事件之间的相似性; 不考虑预测和事实检验,从而不能度量单个语句、感觉或测量信号的信息。
我们先看忽略意义或语义所导致的种种困难。
如果允许我们总结经验知识并赋信号以意义,则即使信源信道可变,我们也可以根据经验知识或信号的意义推测实际发生的X,从而获得信息(见4.2节)。因为Shannon 理论避免考虑意义,信源信道可变时的信息就无法度量。
如果按照Shannon理论度量语言提供的信息,则信息只和语句及事件的概率和条件概率有关,和语义或人对语言的理解无关。若某气象台总是把有雨报成无雨,把无雨报成有雨,而另一气象台总是作正确预报,按Shannon公式,两者提供的信息量是同样的。而实际上,一个人如听信了错的预报,他对事实就更加无知,因而他得到的信息量就应该是负的。
再比如,一个读数不正确的温度表,或一杆斤两不正确的秤,如按Shannon理论度量信息,则它们和正常的表或秤提供的信息一样多,而实际上提供的信息更少,甚至是负的。
控制系统中的信号,比如根据雷达测量数据所做的飞机位置的预测,也是有意义的,控制的依据就是信号的意义。由于经典理论的局限性,涉及意义的信息无法度量,因而预测评价就只能用失真量,比如用均方差作为尺度。
按照常识,失真时信息就少,不失真时信息就多;失真量应能通过信息量得到反映; 常识还告诉我们,把偶然事件预测正确和把必然事件预测正确,两者应有不同的评价。后面我们看到用广义信息或语义信息作为评价尺度不仅可以反映失真,而且可以给更精确、更大胆的预测以更高的评价。
当然,作为客观信息测度,Shannon 信息量也有其重要意义。但是,现实生活中我们更关心主观信息的多少。
Shannon理论要求集合B中皆为互不相容事件。然而,对于语言来说,两个语句,比如“天将下雨”和“天将下大雨”,作为B中元素,从符号的角度来看是互不相容的,但是它们的意义可能是相容的,比如后者蕴含前者,后者出现等价于两者同时出现。这种情况使得用Shannon 理论解决语义信息问题更加不可能。对于感觉或测量信息也有类似情况。
我们再看忽略模糊性或元素之间的相似性所导致的种种困难。
Shannon理论要求两个事件xi和xj 要么完全相同,要么完全不同。若相同的元素构成一个子集,则这些子集构成集合A的一个划分。由于这一原因,用Shannon公式度量语义信息就只能象Carnap等人所做的那样;度量连续信源的自信息就必须在A中强行分类。而现实中,集合A中的事件往往是不同程度上相互类似的。
关于语义信息,比如,“青年人”所指的人就构成一个模糊集合,我们无法给出青年人和非青年人的明确界线。常识告诉我们,一方面,语言的模糊性会减少信息;另一方面,使用模糊语言是一种保守策略,可以减小失真危险。而 Shannon理论无法得出这些结论。
再看感觉信息。比如,有一系列波长连续或相似的单色光构成信源集合A ,显然人眼实际获得的信息和它的分辨率有关,而分辨率又是模糊的。按Shannon理论求X的自信息,我们得将色光强行分类,这样,很相似的色光可能被划入不同的类别,而不很相似的色光反而会被划入同一类别,这至少在理论上是不合理的。并且,由于分辨率模糊性造成的不确定性被忽略了,模糊性导致的信息损失也就被忽略了。
关于测量信息有类似情况。统计物理学熵的度量也有类似问题。
正是因为不考虑事件之间的相似性,才使得连续信源的Shannon熵、相对熵及相对条件熵要么无穷大,要么可能为负值,从而不具有实际意义。
第二章参考文献
[1]Shannon C E. A mathematical theory of communication,Bell System Technical Journal 27(1948),379-429,623-656
[2]陈克艰.上帝怎样掷骰子,四川人民出版社,1987
[3]Kullback S. Information and Statistics,John Wiley & Sons Inc.,New York,1959
[4]孟庆生. 信息论,西安交通大学出版社,1986
[5]周炯磐. 信息理论基础,人民邮电出版社,1983
[6]Berger T. Rate distortion theory, Englewood Cliffs,N.J.:Prentice-Hall,1971
[7]〔英〕 罗斯,钟义信等译. 信息与通信理论,人民邮电出版社,1978
[8]张宏基编著. 信源编码(修订本),人民邮电出版社,1987