附录: 论 文
B模糊集合代数及其用于语义信息和颜色视觉
摘要 用直集I×U上的经典集合代数定义U上的模糊集合代数,所得到的模糊集合代数(B模糊集合代数)遵循布尔代数所有定律,其中隶属度被看作是命题为真的条件概率;任一复合模糊集合的隶属函数可由构成它的各原子模糊集的隶属函数求出，文中介绍了B模糊集合代数在语义信息测度和颜色视觉模型两方面的应用,同时也讨论了它如何用于模糊推理和模糊控制。
关键词 模糊集合;布尔代数;逻辑概率;语义信息测度;颜色视觉模型;模糊推理;模糊控制
流行的模糊集合代数［１］中先定义区间［0，1］上的隶属度运算,再由隶属度
运算定义模糊集合函数。因为［0,1］上的任何一种代数不构成布尔代数,所以由此定义的模糊集合代数也不构成布尔代数;特别是互补律在其中不成立。本文将先定义一种构成布尔代数的模糊集合代数——B模糊集合代数(BFSA),然后由［0，1］上的测度推导出BFSA中隶属演算规律。这一代数和随机集落影理论［２］一致;它已在语义信息,颜色视觉等方面获得应用［３－６］。
1 B模糊集合代数
在BFSA中,模糊集分为原子集和复合集,原子集的隶属函数来自集值统计,并且 一原子集A由隶属函数μA (x)下面的区域(I×U上的子集)确定。复合集的隶属函数则由原子集的隶属函数求出。下面先定义BFSA,再讨论隶属度演算规律。
设论域U,事件x∈U;I=［0,1］,λ∈［0,1］为隶属水平;I×U为I和U的直集;H∈ρ(I×U)是I×U上的清晰集;ψ(U)是U上所有模糊子集构成的集合。
定义1 由ρ(I×U)到ψ(U)上的一一映射为
关于并、交、补运算即∪、 ∩、Ｃ有
根据定义,(ψ(U),∪,∩, c)和(ρ（I×U）,∪,∩, c)同构,后者构成布尔代数,前者也构成布尔代数。
定义2 设B0是I上的Borel域，(I, B0,m)是概率测度空间,x在A∈ψ(U)上的隶属度为
（１）
根据定义,显然有互补律成立:
（２）
对于A,B∈ψ(U),有
(3）
特别是Ａ∩Ｂ=φ（空集）时,
（４）
定义3 称
Ａ(λ)={x|(λ,x)∈HA} (5）
为A的λ水平集或λ截集［７］。
如果总有λ2≥λ1时，
(6)
则称A为原子集［5］。
后面把集合的差“\\”看作是比补“c”更为基本的运算,并且AC和Ａ∩BC只是Ｕ\Ａ和A\Ｂ的不同写法。A\Ｂ可理解为A超出B。
定理1 若A,B是原子集,则Ａ∪Ｂ，Ａ∩Ｂ也是原子集(见附图1);并且(下面省去μ后面的(x)):
(7)
(8)
(9)
证 仅证(9)：
例1
A,B,C是原子集,求
(参看附图)。
解
图1 隶属度运算
图1中，x在A、B、C上的隶属度为a(x)、b(x)、c(x)(参见图1); 垂直线x= x'在
(阴影区域)上的长度就是(x’); 水平线λ=λ'在阴影区域上的部分就是水平集
。
在 BFSA 中若A是原子集,则由μA(x)可以唯一地确定A或HA；若A不是原子集,则由μA(x)不能唯一地确定A。
定理2 设A,B,C，...∈ψ(U)为原子集,则x在任一复合集F(A,B,C,...)上的隶属函数可由μA(x), μB(x), μC(x),...求出。
证 F(A,B,C,...)总可以化为各项互不相交的析取式,比如化成标准析取式,比如化成标准析取范式,而用Demorgon律可使每一项变为下面3种形式的一种:D∩E,D∩Ec,(D∪E) c（Ｄ，Ｅ为原子集）,再按(7)—(9)和(4)即可求出μF(A,B,C,…) (x)。
例2 求μC/(A/B) (x) (A,B,C是原子集)。
解
设A'是隶属函数为μA’(x)的原子集,则有
(10）
这正是Zadeh模糊集合代数中互补律不成立的表示［１］。
2 模糊集的概率论解释及模糊推理
BFSA 中隶属度μA(x)可以被理解为命题“x∈Ａ”在不同置信水平λ等概率发生时被判定为真的概率,即
μA(x)=P(“x∈Ａ”为真)
(11)
设U={ x1, x2,...,xn },x是取值于U中元素的随机变量,则
P(A)=P(“X∈Ａ”为真)= 
(12)
不难看出, μA(xi)也就是条件概率P(A| xi)。
根据概率论,对于
,一般地有
(13)
当A和B极为相关时,上面不等号变为等号,由此可见,隶属度是在假设原子集极为相关时的概率(条件概率)。
可以这样理解模糊集的相关性:让受试者按照两个模糊命题在U中划分使命题为真的清晰集A(λ) ,B(λ) ;当对置信水平的要求下降时, A(λ), B(λ)的外延同时增大,则称A,B相关。可见,在实际应用中,适当地选择由集值统计确定的原子集——只要它们在概念上并不相互对立或排斥,则可以认为对于所有原子集,相关假设基本满足,比如人体特征空间的模糊集{重}和{高}可以同时作为原子集，而{重}和{瘦}不妥。
日常生活和控制系统中常常有“A甚于B则C”或“A超出B则C”的模糊推理,比如:
重而不高为胖,高而不重为瘦;
勇而无谋为莽,悲而不屈为崇高;
利大于弊则可行,湿而无风则有雨;
路远车慢则加速,路近车快则煞车。
对于这些概念演算,用公式
(14)
就比用公式
(15）
更加合理。
例3 设U是车速集合和距离集合的直集,其中有模糊集A={远},B={快},C={加油},D={煞车};下面是给定μA，μB时,分别按(14)和(15)求出的结果如表1所示。
表 1
|
μA |
μB |
μC |
μD |
|
|
|
0.5 |
0 |
0.5 |
0 |
0.5 |
0 |
|
0.5 |
0.3 |
0.2 |
0 |
0.5 |
0.3 |
|
0.5 |
0.5 |
0 |
0 |
0.5 |
0.5 |
|
0.5 |
1 |
0 |
0.5 |
0 |
0.5 |
按式(15),会有
，
同时不为0,意味着加油和煞车同时进行,而按式(14)求出的μC和μD则相当合理。
3 语义信息测度
Shannon 互信息公式无法度量语义信息,因为它不考虑意义和模糊性。已有的其它公式也远非理想。笔者对Shannon 公式稍加改造,得出了一个看来合理的兼涉意义和模糊性的广义互信息公式,使得模糊隶属函数被纳入其中。因为流行的模糊集合论中,隶属度和条件概率相差甚远,并且不能保证在某种情况下使广义互信息公式还原为Shannon互信息公式,而使用BFSA中的隶属可以保证。
设事件集U={ x1, x2,...,xm },可选择语句集V={Y1, Y2,... Yn}; X,Y分别是取值于U,V中元素的随机变量;模糊集
Aj ={ xi | yj (xi)为真}
(16)
我们称P(Aj)是yj的逻辑概率,它不同于yj被选择的概率P(yj)。前者取决于语言的定义,后者取决于人的具体选择;前者不必归一化,而后者必然归一化。
(X)和P(yj | xi)的差别同理。
在Shannon理论中,事件yj提供的关于xi的信息量为
(17）
对于语义信息,应有
(18)
例4 A是人的集合, X=张三,张三20岁。下面是3个不同语句及相应的(xi)、P(Aj)和I(xi; yj)。其中(xi)和P(Aj)来自常识(见表2)。
其中三个语句分别是正确且精确,虚假和非常模糊的例子。可见结果符合常理。
表 2 单位:bit
|
yj |
Ｐ(Aj | xi) |
Ｐ(Aj） |
I(xi; yj) |
|
“张三是年轻人” |
1 |
0.3 |
1.74 |
|
“张三是小孩” |
0.1 |
0.3 |
-1.59 |
|
“张三是大人” |
0.9 |
0.7 |
0.36 |
进一步,用求数学期望的方法可得平均互信息：
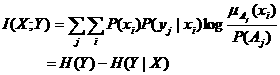
(19)
其中
(20)
(21)
式(19)即为广义互信息公式。H(Y)为广义熵,当V中所有语句互不相容且语句使用正确时,Ｐ(Aj)= P(yj),广义熵就退化为Shannon熵。 H(Y|X)可谓模糊熵;可以证明,当语言极为模糊,即(xi)=P(Aj)时，
H(Y|X)= H(Y)，I(X;Y)=0
当语言极为清晰,即(xi)∈｛０,１｝时,
H(Y|X)=0或+∞(语句虚假时)
I(X;Y)=H(Y)或－∞
常常需要在给定某种条件C*或X的条件概率分布Ｐ（xi |Ｃ*）时,求含有最多信息的语句。即求在P(xi | yj)=P(xi |Ｃ*)时,使
(22)
达最大的隶属函数(xi)。Ｐ（xi | Aj）为yj为真时xi的反条件概率。在限制条件
下,使用拉氏乘子法可得,当
Ｐ(xi | Aj)=P(xi | yj)=P(xi |Ｃ*)
(23）
时,Ｉ(Ｘ; yj)达最大。可以证明上式和
(xi)= KjP(yj
| xi) （Kj是不随i变化的常数）
(24)
等价。这就是说,给定Ｐ(xi |Ｃ*）时,选择yj使(23)或(24)成立可使语句含有最多信息。为使语句更加可信,可选择
(25）
上面分析表明,当事件不确定时,模糊语义可能提供更多信息。
式(23)或(24)可谓语言使用正确的条件。当(23)或(24)成立时,广义互信息就等 价于Shannon互信息。所以说,Shannon互信息是广义互信息的最大上限;仅在语言使用正确时广义互信息等于Shannon互信息。进一步,当语句互不相容时，{ A1, A2,...,
An}是U的一个模糊划分,即{
,
,...,
}是I×U的一个划分,于是H(Y)和H(Y|X)就退化为Shannon熵和Shannon条件熵。
广义互信息公式也可用来度量分辨率模糊时的感觉信息,这时(xi)代表的是两种物性或信号(比如颜色) xi和xj的混淆概率［4］。
4 色觉模型、模糊译码和模糊控制
流行的色觉机制模型都不具有对称性,对色盲机制和色觉进化的解释都不够直观。使用BFSA中的隶属度演方法,可以得出一个对称的,至少在理论上较为理想的色觉机制数学模型［5,6］。
设一种颜色x∈Ｕ，b,g,r∈［０，１］分别是x在B={短波色光},G={中波色光},R={长波色光}上的隶属度,由此可以求出合理的x在8个模糊集{黑色},{红色}等上的隶属度。
下面用
表示Ａ\Ｂ或Ａ∩BC，其他类推。设
M=BG∪BR∪GR， m=μΜ
按新的模型,有（证明从略）
由上面除μ黑以外的7个值就可以方便地求出x的色调,彩度和明度。注意运算的对称性,可见Young和Helmholtz的三色素说和Hering的互补色说在上面式子中得到了自然的统一。略有不同的是这里彩色互补色有三对而不是两对。这一模型也已得到颜色光学数据验证［６］。
因为上述运算方法类似于数字电路中常用的3-8译码方法,所以该模型被称为色觉的译码模型。只是其中使用的是模糊逻辑。由这种译码也可以得到一种模糊控制方法。下面举例说明。
例5 假设为使儿童体格(身高和体重)正常,用食物(肉食和钙片)进行控制,表三中
表示
，其他同理。由表3中4种特殊情况下的控制矢量ci=(ci1, ci2),就可以得出一般情况下(w,h∈［０，１］) 的控制矢量
上式可以保证w,h∈｛０，１｝时，c等于相应的ci。
表 3
|
w |
h |
输出码ei |
肉食ci1 |
钙片ci2 |
|
０ |
０ |
|
1 |
1 |
|
０ |
1 |
|
1 |
0 |
|
1 |
0 |
|
0.2 |
1 |
|
1 |
1 |
|
0.2 |
0 |
比如w=0.3,h=0.8时，=0.2,
=0,
wh=0.3 , c=0.2(1,1)+0.5(1,0)+0(0.2,1)+0.3(0.2,0)=(0.76,0.2)
上述控制方法和已有的模糊推理机中所用方法［９］类似,两相比较,其优点是无须构造输入隶属曲线,输出无须除法（因为
),多输入输出而控制规则不是很复杂时较为方便;缺点是不适于控制规则很复杂的场合。
总之,B模糊集合代数更为与经典集合论及概率论相容,它在诸方面的应用不泛巧妙性,也许读者能发现它在更多领域的应用。
本文在罗承忠教授指导下完成,并受到汪培庄教授的支持和帮助,在此一并致谢。
参考文献
［1］ Zadeh L A. Fuzzy sets， Inform． and Contr. 8 (1985)，338-353
［2］ 汪培庄. 模糊集与随机集落影,北京师范大学出版社,1885,39-47
［3］ 鲁晨光. Shannon公式改造,通信学报, 12 ，2(1991),95-96
［4］ Lu Chen-guang. Shannon equations reform and applications， BUSEFAL 4 ,No.4(1990),45-52
［5］ 鲁晨光. 色觉新说及机制模拟,心理学动态，No.2(1986),36-45
［6］ 鲁晨光. 色觉的译码模型及其验证,光学学报,8 ,2(1989),158-163
［7］ 罗承忠. 模糊集引论(上册),北京师范大学出版社,1989
［8］ Shannon C E. A mathematical theory of communication， Bell System Tech J. 27 (1948)，379-429,623-656
［9］ 钟义信. 信息的科学,人民邮电出版社,1988
［10］ 周炯磐.信息理论基础,人民邮电出版社,1983
［11］ 束越新. 颜色光学基础,山东科技出版社,1981
［原载北京师范大学报(自然科学版),1991年,27卷增2期］