诺贝尔获奖者Arrow的信息价值公式如何荒谬

科研个体户 鲁晨光

作者的信息和信息价值研究：http://survivor99.com/lcg/books/GIT/

Arrow 定义的效用函数是[17]

    (10.2.1)

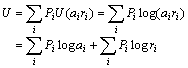ri表示一种投资或打赌的第i种收益，Pi是相应的概率，ai是投资人在第i 种收益(而不是证券)上所下赌注占自己全部资金的比例，是第i种收益发生时，投资人获得的效用。Arrow认为用对数函数作为效用函数较为合理(在Arrow那里，采用对数函数不是因为几何平均收益)，所以有上式。

在的限制下，当矢量(ai)=(Pi)时U达最大，为

      (10.2.2)

而当投资人有了信息后，准确知道哪一种收益将要发生，从而将资金全部投到它上面时，有

            (10.2.3)

信息价值被定义为有无信息时投资的效用差，它正好是Shannon熵，即

    (10.2.4)

看来收益ri表示的是回报――本金加利润。不然负的ri对数是没有意义的。

这个公式和结论流传很广,因为Arrow是诺贝尔获奖者, 得奖是否因为这个结论,我不知道. 但是他最出名的成果就是这个结论. 然而, 这个结论完全荒谬. 因为投资模型荒谬.

请问:我们能够投资某一证券或项目，但是我们怎么能投资于一个项目的某种收益ri？掷骰子打赌可以下注于某个数字，比如2，5，8…., 但是2，5，8……并不表示收益。如果你投资证券，分散也只能分散在不同证券上，而不能分散投资在一个证券的不同收益上。

 

由于这个原因，Arrow的信息价值公式完全是皇帝新衣, 没有任何应用价值。宣扬这一公式和结论的人是人云亦云.

从这个例子看, 不要迷信洋人和权威,哪怕他是诺贝尔获奖者!

 

 

附：

 

关于Arrow的公式和余斌对话

 

（注：余斌在他的书里也批判了Arrow的信息价值公式）

 

鲁晨光：

 

看到你的书了，谢谢，我对Arrow的批判不同

 

不久回国看到你的书了。你的数学好极了。

我对Arrow的批判不同：

 

诺贝尔获奖者Arrow的信息价值公式如何荒谬

http://survivor99.com/lcg/books/GIT/Arrow.htm

 

不知我的《美感奥妙和需求进化》的书是否同时寄给你了。网上地址在这里：

http://survivor99.com/lcg/books/beauty/index.htm

 

 

余斌   

 

  发表: 2005-09-03 09:55:53 第2楼

 

你关于美感奥妙的分析符合历史逻辑，我非常赞赏。真是一本好书。但是我一直都比较忙，没能好好阅读。

 

余斌 :

  发表: 2005-09-03 10:05:02 第3楼

 

你对诺贝尔获奖者Arrow的信息价值公式不同看法是正确的。但如果不把Arrow公式用于证券投资，而仅仅用于他所示例的赌博，则他的信息价值公式还是成立的。对于某种赌博，包括买彩票，我们投资的的确是其中的某一种结果。

 

鲁晨光  :

 

还是有问题。

在折骰子打赌中，我们下注的是点数，不是赔率（本益和/本）。把点数换成赔率好像不行，因为同样的赔率，点数有多种。

假设一种赔率对应一种点数， 两者赔率和发生概率的乘积一般等于常数（如果不等，大家都会选择乘积较大的i），常数等于1（或略小，因为庄家占先）。对于这样的赌博，Arrow的公式：平均效用＝sum pilog(airi)＝-sumpilog(aipi)(假设常数＝1）

可见，Arrow模型和真实赌博相差很远。

 

再者， 按Arrow说法

信息价值V=U2-U1

无信息时的效用 U1= sum pi log(ai ri)

有信息时的效用U2=sum pi log ri'

但是，U2是不对的，因为知道i'发生， U2应该是 log ri'。

所以从哪个角度讲，Arrow的分析都是错的。