四色定理简洁证明及其漏洞

鲁晨光

http://survivor99.com/lcg

四色定理：任何一张正规地图（每一点最多和三个国家相连）只用四种颜色就能使具有共同边界的国家着上不同的颜色。

证明如下：

假设存在一个数目N, 国家数目达到N时， 就可以构造一个地图――它必须用五种颜色着色（四色不够）。这也就是假设去掉其中任何一个国家，数目成为N-1时， 它应当可以用四种颜色着色。

现在我们用反证法证明。

假设我们能够证明：如果N-1个国家的地图能用四色着色， 把去掉的一个加上去也能， 那么我们就证明了不存在这样一个N, 也就证明了四色定理。

根据欧拉定理, 任何一个地图， 必然存在一国（称之为X国）， 其相邻国家数目不大于5。 或者说， 其邻国可能是1个， 2个， 3个， 4个， 或5个。

这样，我们就从N国地图中拿掉X国，这时它应当可以用四色着色。现在，如果我们能证明，把X国放回到着好四色的N-1国地图中， 通过系统颜色变换，也能用四色着色， 这样就证明了四色定理。

假如X国邻国只有1，2，3国， 这是简单的，着第四种颜色就是。现在考虑四邻国和5邻国。

前人已经通过2色通道的概念，证明四邻国可以为X国着色而不增加颜色数目。参看图1 （其中R,G,B,Y分别表示红，绿，蓝，黄四色）

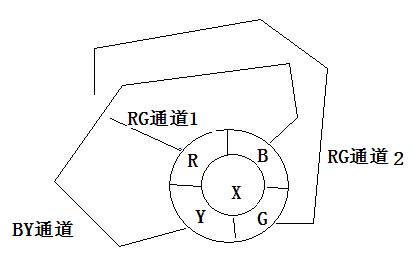
图1 四邻国问题

一个二色通道是由交替着上两种不同颜色的国家连成的。上面两个通道BY通道和RG通道总有一个是不通的。 假设RG通道不通， 则把和R国以及与之相连的RG通道1上的国家的颜色R和G互换，再把X国着上R就行了.

着好色的地图如图二。

图2. 四邻国问题解决

剩下的硬骨头是5邻国问题。我们假设最坏的情况――X邻国已经有四种颜色。现在我们可以画图三所示四个通道。

图3 五邻国问题

1）BY通道是通的， RG通道必然不通， 这好解决――改变与G国相连的RG通道颜色，再把X着色成G就行。

2）BG通道是通的，RY通道必然不通， 这也好解决――改变与Y国相连的RY通道颜色， 再把X着色成Y就行。

3）BY通道和BG通道都不通， 则RG通道和RY通道必然是通的。即如果下面两个通道不通， 则上面两个通道必然是通的。这时，我们把和左B相连的BY通道(a)颜色对调，和右B相连的BG通道(b)颜色对调，然后把X着成B就是。参看图4。

图4 五邻国问题解决

到此5邻国问题圆满解决， 四色定理证明大功告成。

这是我20年前的证明。当时我没看到Kempe的具体证明， 也不知道别人提出的反例究竟如何。我把它投寄给一位再报上介绍四色定理的数学学者， 他也没发现漏洞。后来倒是我自己发现了漏洞――图3中如果上面两条通道交叉，证明就会失败。参看图5。

图5 上两个通道交叉导致证明失败的反例

具体图例：

图6 反例

我把这个看似简洁正确方法公布出来，或许可以让后来者少走弯路。