![]()
张学文 zhangxw@mail.xj.cninfo.net
所谓对数正态分布是指变量x的概率密度的分布函数f(x)满足下面的关系
![]() x>0,(18.2.1)
x>0,(18.2.1)
这个公式与正态分布公式类似。但是系数部分的分母上多了自变量x,另外,在指数部分的x处变成了该变量的对数值了。这里的常数a,σ
的含义有变化。a是变量x的对数的平均值,σ是变量x的对数的标准差。由于对数仅能用于正实数,所以变量x必须是大于零的数。f(x)就是变量x出现于x-0.5到x+0.5
范围的概率密度。
现在用最大熵原理配合约束条件推导这个公式。
由于变量必须大于零,与公式(18.2)对应的约束条件变成了(积分下限变了)
![]() ,x>0(18.2.2)
,x>0(18.2.2)
一个新的约束是变量的对数的平均值a是固定值:
![]() ,x>0(18.2.3)
,x>0(18.2.3)
这个公式与幂分布问题中的公式(17.18)类似,都体现了变量的几何平均值为不变量。记住这个物理含义会帮助我们理解问题。
另外一个类似正态分布的约束条件就是变量的对数的标准差为固定值,即有
![]() ,x>0(18.2.4)
,x>0(18.2.4)
根据拉哥朗日方法,定义一个新函数F:
![]()
上面公式中的f就是f(x)
。
对最复杂原理的利用体现在上式对f的偏微商应当等于0,于是得到
![]()
利用(18.2.2)、(18.2.3)、(18.2.4)这些约束关系可以解出三个常数 C1,C2,C3,经过整理就得到对数正态分布公式(18.2.1)。
上面的推证是在变量必须大于0的必然要求下进行的。如果变量不仅是大于0,而且是大于某个正数b,上面各个公式中的积分下限就改为b。这实际是把坐标向右移动了b。与此对应的概率密度公式是
![]() ,x>b
(18.2.5)
,x>b
(18.2.5)
这样我们就利用最复杂原理配合这些新的约束条件得到了概率论中所谓的对数正态分布函数。图18.2给出了这个公式对应的曲线图,它是一个单锋偏态曲线。
图18.2对数正态分布图
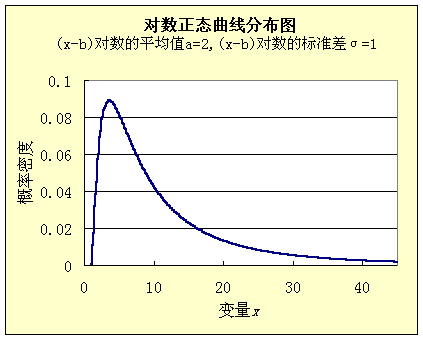
(对数正态的约束条件是我们在1992年的《熵气象学》一书中给出的,那里的推导工作是马力同志做的。至于是否有人在更早给出过我不清楚。写本稿时笔者把有关推导又做了一次。为节约篇幅,这些具体推导过程没有列出。)
下面用汉字笔画问题作为对数正态分布的示例。
中国汉字有的笔画多,有的笔画少。把所有汉字看作是一个广义集合,把每个汉字看作是一个个体,把汉字的笔画看作是标志值,于是就提出了不同笔画汉字各有多少的问题或者说关于汉字笔画的分布函数问题。
笔者在2000年猜想汉字笔画多少与该笔画的汉字的数量之间可能是对数正态分布。于是就对大量汉字资料做统计分析,发现汉字的笔画x与该笔画的汉字数量g确实符合对数正态分布公式。
要研究不同笔画的汉字各有多少当然是翻字典。但是现代字典多数是以拼音为主线编的,统计起来很费力。为了便于统计,笔者用了辞海[辞海编辑委员会,辞海,上海,上海辞书出版社,1979(1987年印)]。
表18.1.是词海中统计出来的不同笔画的汉字的个数。它显示出笔画过少或者过多的汉字都比较少,9-14画的汉字最多。
表18.1.不同笔画的汉字的个数
|
笔画 |
个数 |
笔画 |
个数 |
笔画 |
个数 |
|
1 |
3 |
13 |
1307 |
25 |
65 |
|
2 |
23 |
14 |
1188 |
26 |
34 |
|
3 |
74 |
15 |
1125 |
27 |
27 |
|
4 |
163 |
16 |
956 |
28 |
19 |
|
5 |
261 |
17 |
788 |
29 |
9 |
|
6 |
464 |
18 |
567 |
30 |
4 |
|
7 |
823 |
19 |
495 |
31 |
3 |
|
8 |
1084 |
20 |
370 |
32 |
0 |
|
9 |
1281 |
21 |
264 |
33 |
2 |
|
10 |
1357 |
22 |
208 |
34 |
0 |
|
11 |
1445 |
23 |
159 |
35 |
1 |
|
12 |
1571 |
24 |
121 |
36 |
1 |
为了检验汉字的笔画与汉字的数量的关系是否符合对数正态分布,我们先把相对密度形式的对数正态分布公式乘以汉字的总个数N,就得到了密度形式的分布函数公式g(x),
![]() (18.2.6)
(18.2.6)
这里的g(x) 表示笔画为x的汉字的个数。公式中16262是汉字(辞海)的总个数N, a是汉字笔画数x的自然对数的平均值,其值为2.4739,σ是汉字笔画的自然对数的标准差,其值为0.3827(平均值和标准差的计算公式请看第七章)。这个公式可以计算出各个笔画的汉字的理论个数,它与实际资料的对比效果显示在图18.3中。
图18.3.不同笔画汉字的实际数量(深色)与理论数量(浅色)的对比图
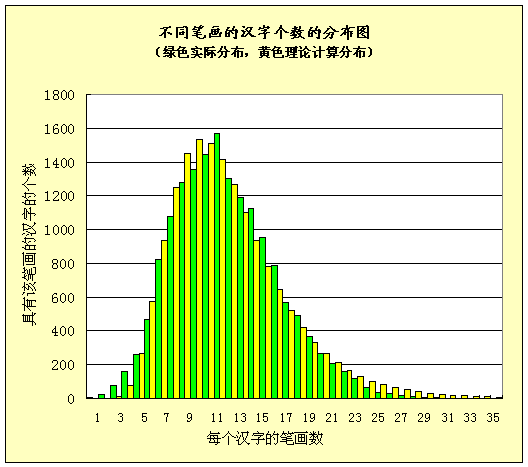
图18.3.中汉字的笔画数(从0-36画)列在横坐标上,而立柱的高度(纵坐标)代表了该种笔画的汉字的个数。深色是资料中的实际值(即表1.
的值),浅色是数学公式计算的理论值。
从图18.3 中看理论公式与实际资料的拟合是相当好(存在很小的趋势性的偏差)。浅色(理论)与深色(实际)的基本走势和具体的数值都比较接近。一个仅含三个参数(N,a,σ)的理论公式与这么多数据基本一致说明这个公式准确刻画了汉字笔画与数量的关系。
图18.3说明我们可以用这个公式代表汉字笔画与汉字数量的关系。这对于汉字研究显然有理论价值。
为什么想到汉字可能符合对数正态分布?笔画少的汉字和笔画过多的汉字都比较少的事实提示笔者它可能是正态分布。另外几何平均值为固定值的考虑(见第十七章幂分布)可能也符合汉字。确实,把这两个提示归结为两个约束条件利再考虑最复杂原理适用于汉字笔画问题,就把我们引导到对数正态分布这个模型中。当然最重要的理由仍然是这个模型确实符合汉字的实际。
汉字是几千年慢慢形成。它竟然可以用数学公式描述笔画与字数的关系,并且可以讲出一些理由来,这出乎一些人的预料。我们认为这体现了最复杂原理对与一切有随机性的事物有约束力。
多少人在欣赏书法家写的汉字的体型美,多少人赞叹数学公式之美,把汉字的笔画数与该笔画的汉字的个数联系在一起的竟然是一个光滑的可以用解析式表达的数学公式,这就是汉字的数学之美了。人们对汉字体形之美已经了欣赏多年,汉字中蕴藏的数学之美显然也应当去发现、分析和掌握。
拼音文字,例如英文,也可以分析类似的问题,但是在那里要分析的应当是所有单词中由不同字母组成的单词各有多少。英文是这样的吗?欢迎读者去做分析。我估计也应当是这样。
读者掌握了对数正态分布的形成的物理原因,就容易发现符合这些条件的客观事物,从而发现客观事物中的定量关系(规律性)。“知识就是力量”。