第三篇应用

前面两篇通过引入新的概念和原理已经组成了一个不大的知识框架（一个简单的认识客观事物的模型）。它可以概括过去的很多认识，也帮助我们更主动地去分析更多的事物。本篇要从应用的角度指出某些学科中的某些工作就是本模型的应用，也分析它可能的新应用领域与新的应用前景。

 第十六章三个概念的应用

（2001年9月公布于 http://entropy.com.cn ）

  §16.1 广义集合概念的应用

为了便于分析很多客观事物的组成问题，我们引入了广义集合概念。组成问题在气象，统计物理、概率、统计等很多自然科学中广泛应用，所以把广义集合再用到这些学科都是顺理成章的事。确实，有了广义集合概念再加上通用的分布函数概念对理解统计物理中的一些具体事物和分布有事半功倍之效。由于可以用广义集合概念定义概率、可以把概率分布看成是这里的分布函数的特例。所以，概率论和统计学的很多应用也都是广义集合的应用。广义集合、分布函数、复杂程度等等概念充实了概率与统计领域，也使概率论和统计学的知识更容易理解和学习。

物理学教授王彬指出（《物理与工程》，2001年第1期，17-21页）：力学原理帮助我们去分析恒星的轨道为什么是椭圆的，苹果为什么从树上自由落下．熵的原理帮助我们去理解为什么自然现象恰恰是这种分布律而不会是别的分布律．

如果我们只讲质点的一两个运动方程：匀加速直线运动方程，谐振动方程，而不讲牛顿运动方程，这显然是只见树木不见森林的做法．热学只讲系统的一两个分布函数：麦克斯韦速率分布律、玻耳兹曼能量分布律，而不讲最大熵原理．不能不令人遗憾地指出，这种只讲现象不讲分析原理的做法，无异于只见树木不见森林．

1991年笔者说“统计物理中的深刻思想，不应当仅供物理学家独享，它实际也是众多学科共享的理论武器，它会帮助众多学科向理论阵地迈进一大步”（在《熵气象学》一书中）。广义集合概念（连同分布函数等）使统计物理从满页公式和神秘概念中解脱出来了，我们相信在它的帮助下使其他领域借用统计物理学的概念和方法会容易很多。

 在1999年写的一个网页文章中笔者说“我们已经继承了牛顿很多的科学遗产，但是我们仅是承认麦克斯威的成绩而不是去学习他在处理“复杂”问题的基本思路，我们也就放弃了很大的一份科学遗产”。1999年麦克斯威又被公众评定为千年的10名思想家之一（第9）。我们认为广义集合概念的提出对推广麦克斯威的思想方法是有好处的。

集合概念可以描述一个物品的成分（组成）有那几种。广义集合进而描述每种成分占的数量是多少。在介绍广义集合时我们已经列举了大量的事物都可以看成是广义集合的例子。无论是玩的每手麻将牌、吃的每付中药或者西药、每次考试的全班成绩、每个原子或者分子构成等等等等都是。理解这个概念的读者再举很多例子都没有困难。

特别要强调的是广义集合概念不仅是可以用到物理和概率以外的自然科学，它也完全可以顺利地用到社会科学中。马克思早就提出要把数学用于社会科学。如何用？广义集合概念的应用是一个方面。

笔者不是数学工作者。提出广义集合这个有数学味道的词仅是迫不得已的冒风险的行为。我们强调目前它的应用重点是在自然科学中而不是数学中。这个概念在数学方面如何应用，除了第六章讨论到的广义集合多项式以外笔者没有更多的想法。如果数学界认为这是不能容忍的错误，希望指出；如果认为这个提法打开了一个数学上的新园地，希望大家培育开发。

集合概念在数学里是基础概念。但是目前在物理学化学等这些自然科学中使用集合概念表述自己的研究对象的情况比较少，有了广义集合概念不仅简化了对很多自然科学研究对象的表述，也使集合二字借着广义集合这个词汇迈入各个自然科学。

§16.2 分布函数概念早已应用

我们已经介绍了很多广义集合。要把每个广义集合具体的表示清楚就得知道它的分布函数。广义集合的具体定量应用必然用到分布函数，所以分布函数的应用领域和广义集合一样宽。

从科学历史角度看，分布函数早已没有点名（或者半点名）地被广为应用了。太阳光有很多颜色，科学上就问不同的波长（或者频率）的光子各有多少。这是统计物理学研究的问题，它称为黑体辐射的能量分布问题。在统计物理中类似问题还有不少。从我们的角度看这都是分布函数的特例。所以说分布函数在统计物理中早已应用并不为过。

概率分布问题是概率论的重要内容。概率分布又在统计学中得到了广泛应用。而我们使用的分布函数把概率分布看做是自己的特例。所以概率论和统计学的应用也说明分布函数早已广泛应用了。关于这方面的具体情况在概率论和统计学有很多介绍，我们现在的任务仅是指出这个关系，而不是重复介绍这些比较成熟的知识。

我们没有强调分布函数是自己的创造，但是从广义集合入手引入分布函数概念就比各个物质科学就事论事超脱一层。分布函数概念是统计物理中的各种分布的泛化。在抽象领域一次性地理解了什么是分布函数就为物质科学中一个个的介绍具体分布带来了很多方便。

现在小学生就明白什么是百分比。已经非常普及的电子计算器大多设有专门的功能键去计算百分比，这也说明百分比的应用范围非常广。计算不同成分（组成）占的百分比就是求一种分布函数的数据。所以分布函数的应用范围应当与百分比的应用范围一样宽。研究分布函数规律也就包含了对百分比的研究。它们是描述客观事物组成的定量语言。

§16.3 用分布函数归纳现象

“观察客观事实”是很多科学工作的起点。观察结果经常是写出报告，可能还罗列很多数字。科学工作的另一个重要内容就是从观察的客观事物（现象）中整理归纳出客观规律。如何从大量的现象中提升为精练的规律？这里好象没有明确的道路。如果研究者头脑里没有合适的、精确的定量的概念，就很难把现象升华为规律。具有了广义集合和分布函数概念以后，你也就自然地具有了概括一大类客观规律的一般思路（当然远不是全部）。它几乎可以把你领到规律的门前，它使你感到发现客观规律的事没有那么神秘，只要用心和努力，也可以有所收获。确实分布函数是概括归纳某些（当然不是全部）客观现象使之提升为规律的好工具（思想工具和数学工具）。

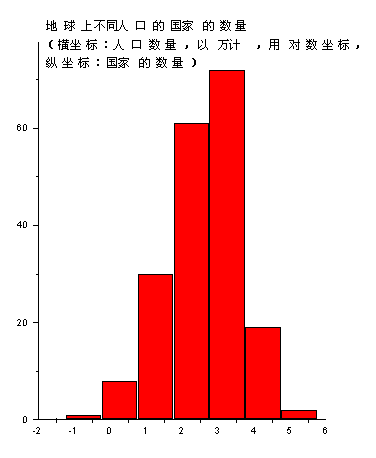
地理书籍中有关于国家名称和国家人口的资料。这些资料是事实，也很重要，但我们不好说它就是客观规律。如果有了广义集合概念，就可能想到把地球上的国家作为总体（广义集合），把每个国家作为个体，把该国的人口数量作为标志变量。有了各个国家的人口资料，我们就可以统计不同人口的国家各有多少。而这个问题符合分布函数的定义。

下面的直方图就是利用浙江电子音像出版社出版的世界知识百科光盘提供的各国人口数据而绘成的。由于各国国家的人口数量从12亿（1.2×10⁹）到数千人，这个人口的变化幅度过大，我们是把以万计的人口数量取对数再做为横坐标而后绘成图的，其纵坐标表示人口数量在各个区间内的国家的数量。此图清楚地表明世界上人口过少人口过多的国家都比较少。多数国家的人口在100万到1亿之间。

这个直方图是用离散变量描述现象的，但是本问题更象一个连续变量的问题，于是可以进一步问：能够用一个连续变量的数学公式拟合它吗？既可以为地球上的不同人口数量的国家各有多少问题找到一个定量公式吗？进而还可以问：可以提供一种理论说明为什么它会是这样的分布（组成）吗？很显然，没有分布函数概念你迈不出这一步，更不要说利用理论解释它了。看来，认真统计出人口数量与国家数量的关系，就得到了一个客观规律（对客观事物做了科学的归纳和表述）。而这一切都是在有了广义集合和分布函数概念之后变得既简单又明朗的。广义集合和分布函数几乎把规律送到了你的面前。

当然有了这些概念还有一些具体的计算技术和技巧，好在现在有很多统计书籍和软件（例如微软公司的Excel，Microcal公司的Origin）可以帮助我们， 这些具体问题也很重要，但是这不是本书的任务。

又例如，把进商店买了商品的人的总体看做是一个广义集合、把每个顾客看做是个体、把买的商品的价值看做是标志变量，就可以进而分析不同的购买力的顾客各有多少。而这就构成了一个分布函数。它描述顾客是由那些购买力的人组成的。对这个分布函数进行研究当然是有必要的。下面给出的一个分布函数就是根据某医药公司在一年间的8321次售药记录而做的统计(横坐标表示购买力，元，的对数；而纵坐标表示该购买力的顾客人数）。这个分布函数就是一个客观规律。尽管它是针对某年某个公司的，但是它也反映了一般的购买力的规律性。我们甚至也可以为它寻找一个连续变量的数学公式或者进而找出理论说明。

 
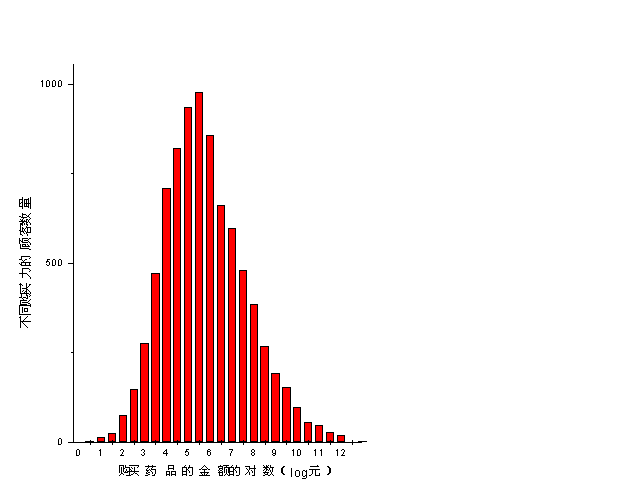
据说数学已经把经济学家武装到了牙齿，这个例子可能对他们仅是陈年旧事。但是也可能因为由于没有分布函数概念而没有想到这个方面的定量规律（定性的认识肯定有）。我们强调的就是广义集合和分布函数概念会帮助我们很快地科学地发现客观规律。这包括科学地提出问题、恰当的分析问题、理清什么是这里的个体和标志变量、迅速地得到规律（经验公式、唯象关系）。

中国字有的笔画很少，有的笔画很多。有了广义集合和分布函数概念我们就容易形成这样一个问题：把中国汉字作为总体（一个广义集合）把每个汉字作为个体，把组成该汉字的笔画的数量作为标志变量，问不同笔画的汉字各有多少？研究中国汉字的人很多，想到这个问题的可能就很少。笔者2000年利用《辞海》分析了这个问题，发现不同笔画的汉字符合所谓对数正态分布（统计学中的一种分布），后面（第18章）我们要用最复杂原理说明为什么它会是这样。

细心的读者如果是某领域的专家，有着丰富的资料、丰富的专业知识，一定可以想出一批没有研究过的分布函数来。从一定的角度去归纳、证实一个研究对象的分布函数，就是一个研究成果，这几乎也都可以写成一篇论文。

我们在第四章就提到了过去的科学分类中的上百个广义集合的例子（它们也代表了上万、10万的例子），它们当然也是分布函数在各个领域的例子。我们在第五章把广义集合分为六类。这些一般概括既是帮助大家理解广义集合和分布函数，也是希望读者掌握它们，达到举一反三，自己去发现分布函数（规律）的目的。

归纳客观现象的方法有很多，我们强调利用分布函数归纳现象也就是发现了客观规律。确实，科学活动的一个重要目标就是发现客观规律，形成准确的概念和良好的模型可能是做出发现的前提。广义集合（包括明确什么是广义集合，什么是个体和什么是标志变量）就是一种合适的概念，也提供了一个认识模型。而具体得到该广义集合的分布函数就是发现了客观规律--在这里概念与规律的关系比较简单明确。

人们研究了各种来源的水，发现它们都是由两个氢原子一个氧原子组成的。按照我们的观点，这就是得到了水分子的分布函数。写成化学分子式是H₂0，写为广义集合多项式就是 水={2H+0}。由于所有分析过的水都是仅由这两种原子按照2：1这个比例组成，这也就是一个客观规律，即化学家每知道了一种分子的组成，就是发现了一个客观规律。

麦克斯威给出了一个很复杂的公式（见下一节）描述了不同运动速率的气体分子各有多少。它符合分布函数概念，又被实验证实符合实际。这个公式显然是一个客观规律。

得到规律的道路有很多，利用广义集合和分布函数概念的密切关系是得到客观规律的一种简单又快捷途径（注意，它不能概括全部规律！）。

§16.4偏见、愚见与卓见？