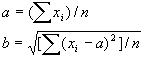
统计学里经常是根据出现的情况（一批试验观测数据）去推断一个结论（如显象管的平均寿命）。这种推断并没有绝对的把握，人们是退而求其次：以概率最高的事件作为正选答案。
概率公理没有说高概率的事件必然出现，仅是说概率最高的事件是最容易出现的事件，所以不要误以为它就是概率最高的事件必然出现。它的含义仅是比其他的事件容易出现。它与2+2必然等于4是不同。 实际上如果概率的最高值是0.6，它仅意味着在1000次实验中大约有600次是正确的。如果概率的最高值是0.99999999或者更高，情况就好了很多，它意味着在10次或者1万次抽样中都难得错一次，这已经与必然出现没有什么差别了（在实际的意义下不是理论意义下）。统计学里有个很高明的最大似然原理（方法）。它的理论根据就是“在一次随机抽样中，认定最容易出现的事件是概率最高的事件”，即概率公理。由于最大似然方法是理解概率公理一个好事例，这里做些介绍。
统计学中有时已经知道某些数据来自某个广义集合（过去称为母体），而且知道它的分布函数（对应过去的概率分布函数）是什么形状。问题是要从一批随机抽样观测数据中去推测该分布函数中的统计参数（例如平均值）是什么。最大似然方法就有一套处理这类问题的有效方法。
下面问题是个比较具体的例子：已经知道成年人的身高服从正态分布（很高和很矮的学生很少，身高与平均值接近的学生最多），又对100人测量了身高。问描述身高的正态分布函数中的两个参数----平均值a和标准差b各是多少？这里说的正态分布就是统计学中著名的高斯分布。它也是连续变量型的相对分布函数中的一种，其数学公式是
（10.1）
我们用f(x,a,b)表示这个正态分布函数，x 代表身高，a,b
是目前还不知道的参数值（平均值和标准差）。把公式写成这种格式是突出a,b的值现在还不知道，它也是未知数。而已经知道的是100个人的身高的数据。现在的问题是如何从这100个数据中反求出
a,b 的估计值（称为最大似然估计）。
设100个数据是 x1,x2,...x100,
对于x1其出现的概率为f(x1,a,b)
对于x2其出现的概率为f(x2,a,b)
...
对于x100其出现的概率为f(x100,a,b) 基于以上观测事实，根据独立事件的乘法定理（每次采样都与其他的采样无关），100个数据恰好是x1,x2,...x100 的概率P 显然是这100个概率的连乘积。所以有下面的等式P=f(x1,a,b)f(x2,a,b)...f(x100,a,b)
这个等式也可以写为
P=∏f(xi,a,b) （ i=1,2,...,100） （10.2） 即这个概率P 是另外100个概率值的连乘积。∏是连乘积符号，在这里就是100数连乘。 表面上看概率P 现在是100个x 值的函数。但是100个x 值已经观测到了。真正不知道的是a，b 的值。现在要利用对概率的分析去推断a，b 的值。 显然，如果100个学生的身高是另外一组数值，它们对应的出现概率P 的值也会是另外一个数值。这100个观测数据为什么是这100个数值而不是别的？这说明这100个数值最容易出现。 如果把这100次测量统一看成一次抽样作业，根据概率公理显然表明：100个数值恰好是这一些数值（是不是别的）的事件所对应的出现概率应当是最高的概率。 现在我们的思路一转：就是要根据“概率最高”这个结论反求出我们现在还不知道a，b 的具体数值是什么。----这就是统计学中最大似然原理（方法）的核心。 公式（10.2）左边的概率值应当是概率的最大值，而它又是a 和b 的函数，在数学上我们自然认为概率p 对a 和b 的偏微商（数学中的微积分知识）必然分别等于零。显然我们应当利用这个关系反求出a，b 的值。注意到
1.公式（10.2）右边是100数的乘积，它处理起来很麻烦； 2.一个数的对数与原来的数是单调函数关系，所以求100个数的连乘积的最大值与求它们连乘积的对数的最大值是等价的； 3.把公式（10.2）两边取对数后再求最大值在数学上容易计算。 我们对公式（10.2）的两边先取对数，再分别对统计参数a，b 求偏微商，由于概率最大（根据概率公理）时上述偏微商必然分别等于零。利用这两个等式就可以求出未知的参数a，b 。它们分别是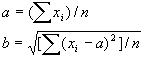
最大似然方法在统计学中得到了广泛的应用。其具体步骤可以从对应的统计书中找到。这里不代替教科书去介绍它了。大家明白用最大似然方法求得的结果比较有效的原因是它利用了概率最高这个条件。而选取“概率最高”为条件是因为它符合概率公理。
最大似然原理（方法）富有成效的原因是它巧妙地利用了概率公理。
最大似然原理是早就明确了的原理，而概率公理是现在才提出的原理。没有概率公理以前人们认为最大似然原理的思路很巧妙很合理，现在有了概率公理人们就认为最大似然原理是概率公理的一个重要推论和应用。有了概率公理，我们就向随机性事物的基本规律方面又迈进了一步；就多回答了一个为什么。