系统何以立论

系统何以立论？

王笛兴（ wangdixing@sina.com )
在 http://entropy.com.cn 公布于2002.02

一、引言

系统科学的开创者贝塔朗菲在《一般系统论的历史与现状》中指出：“基本的系统问题”可以用亚力士多德的古老命题“整体大于它的各部分的总和”来表述。全部系统研究的目标和任务集中到一点，就是阐明整体为什么大于部分之和，制定描述大于部分之和的那些整体属性的科学方法。

“整体大于部分之和”是一种形象的说法，并非科学表述。这个基本的系统问题较为科学的表述应当是：若干部分按照一定方式相互联系起来形成系统，就会产生出一些只有整体才具有的新属性，这些整体属性不可能还原为低层次的属性。与传统科学相比，系统科学的特点就是在于强调把握整体的或高层属性。

为解决这一问题，贝塔朗菲首先提出“突现”概念，把整体“多于”部分之和的那些属性称为系统的整体突现性。至于什么是突现？系统为什么要突现？突现的运作机制是什么？能否用数学工具描述突现？如何利用计算机模拟突现？等等，可以说都还没有定论。中西方的很多研究大家通过长时间的研究之后都感到困惑。

“ 突现 ” 是系统或自组织的基本问题，能否对其描述，被认为是对人类认识能力的新挑战。客观世界的突现性是否超出科学理论的能力范围？存在认识突现现象的知识限制吗？我们能够科学地刻划突现性吗？这是系统科学必须回答的理论问题。美国的圣菲（ SFI）学派曾就此举办关于《知识的限制》研讨会（1989）。会上鼓吹 “ 科学终结论的” 人把突现看作超越科学能力的现象，霍根甚至把科学界现在提出研究突现性问题本身当作科学终结的证据。霍兰在《涌现》一书中则视之为建立突现论科学的心理障碍（见参考文献 1中第177页）。为解决上述问题，系统理论不能仅限于定型描述，必须解决系统悖论问题，必须给出系统的共性定量形式化或自组织原理描述。

二 、复杂系统的定量形式化描述

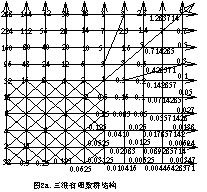
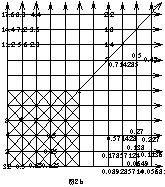
描述系统有三个要素：①、因子。②、结构。③、结构法则。构成系统的单元因子可用参量描述，单元因子的作用关系可用结构描述。显然，结构的构成要遵循一种法则，这种法则即参量之间的交互作用法则，或者说是系统产生“整体大于部分之和”的涌现性法则。就是说，关系及结构并非无原则建立，如整数集根据加减运算法则可构成加减运算关系结构，有理数集根据乘除、乘方开方、对数反对数运算法则可构成乘除、乘方开方、对数反对数运算关系结构，其描述模型统称“准全息元数学模型”，见图1图2 ：

模型反应整数之间的加减运算关系、有理数群之间的乘除、乘方开方、对数反对数运算关系，实数之间的乘方开方、对数反对数运算关系。三者之间即具独立性，又具逻辑相容统一性；可描述不同类型及多元相容一体化的复杂系统。

描述复杂系统，因子、结构、结构法则缺一不可。系统不能仅用非线性方程或公式表示，更不能单纯用语言描述，而一定要用具体参量的具体关系（结构）表示。一个极其复杂的状态转换系统，其共性描述模型必须以可能的状态（参量）为背景――如整数、有理数、实数及超越数，建立普遍性的内在联系――如加减乘除、乘方开方、对数反对数运算关系为基础。并在此基础上转换这些关系，包括参量之间的互相控制、交换等，其中最基本的关系，是参量基于运算关系的互为因果交互作用关系。这种关系可反映系统足够的复杂性，可反应诸如神经系统的本质共性。而不同程度及不同类型的系统属性都可在此基础上派生，或相容于此。

模型充分体现了系统的自组织原理，所谓的自组织，是整数集、有理数及实数集按加减、乘除、乘方开方、对数反对数运算关系组织起来所体现的整体不可还原属性。自组织意味着涌现，如整数依据加减逻辑法则自组织，即可涌现加减运算功能。自组织意味着进化及创新，且能够积累保持创新成果。自组织有两种基本类型：一种是交互作用型，系统参量呈互为因果关系；一种是协同作用型，系统参量呈整合关系。前者如人脑的中枢神经网络或联合国，具有参量的组合与分解――即逻辑思维功能，后者如各种感官的神经网络或一个国家内的行政组织，具译码整合分类――即形象思维功能。在人脑神经系统中，两种类型的自组织具有相容统一性。对这些属性的有效描述，是系统得以立论的基本前提。

根据同构相似性原理，系统不论多么复杂，总能找到同构描述模型。系统得以立论的基本前提，就是不但能够给出复杂系统的共性定量形式化描述，且能据此构造人工系统，使复杂系统的功能及各种本质特性得以再现。如以模型为逻辑结构模式，利用微电子技术，或生物芯片技术物化为人工神经元网络，即可构成以基本运算功能为基础的刺激反应模型――具有人脑中枢神经网络的所有本质结构与功能属性。如自适应、自调控机制；反馈循环、及自适应稳定机制；因果关系变换的预先矫正、及信元之间的自组织或功能耦合机制；这些机制是体现智能的基础，也是学习及创造性的基础。其可逆性及两极互变性，亦符合辩证逻辑法则；其结构的创生，符合生物进化原理。作为复杂系统的描述模型，它不象热力学所预言的那样趋向无序，而是自发地按特定法则，在开放有序的基础上更加有序。相对而言，是人工系统的有效数学理论基础。

通过准全息元数学模型，我们对于自组织及涌现性产生的机理，对复杂系统整体与局部的关系 ――尤其是非线性作用机制，就会有一个非常明确的认识。非线性尽管是多种多样的，但只要找出描述它们的共性方法，就能够在科学实践中解决大量实际问题。所谓的非线性，其实质是非整数参量体现在物理系统中的非加和性交互作用或转换机制――如有理数或实数集的乘除、乘方开方、对数反对数逻辑运算机制。

作为复杂系统的共性描述，模型可体现复杂系统的三个基本定理：①、准完备性定理。②、结构法则的多元相容性定理。③、自组织参量的互为因果关系定理。可体现系统创生的三个基本原理：①、结构法则（等价逻辑法则）内涵与外延的一致相容原理。②、互补原理。③、自组织原理。或者说：①、准全息信元逻辑相关原理。②、自组织功能耦合原理。③、准全息信元逻辑内函与外延一致性及多元相容性原理。如果说复杂系统有一般性原理的话，那就是上述原理的总和。

三、准全息元数学模型体现复杂系统的基本特性

模型可进行参量的一致有效性因果逻辑关系变换――元逻辑运算；不同的运算关系之间，具有因果逻辑关系变换的层次性，及相容性，具有质变与量变的统一性；及如下一些基本属性，这些都是描述复杂系统结构极其复杂，并具稳定与有序开放的基本前提。

①、准全息性

准全息概念，不同于所谓的全息概念，全息概念相对于系统的动态或静态描述，事实上都不存在，即全息不全。全息意味着系统是个不再进化的死系统，可以进行穷尽描述。所谓的准全息，是系统在相容已有结构法则的基础上，能一致有效地内涵或外延建构，系统编译码输入输出及处理信息的能力可以延伸或增强――即信息量可扩展，故谓准全息。

②、准完备与开放性

系统的结构法则具有内涵与外延的一致性，决定了系统具有开放性与准完备性。开放及进化是系统准完备化的基本前提。在封闭系统中，哥德尔用有穷方法已经证明其具有不完备性，被称为形式系统的不完备性定理，但不完备性定理不适用于开放系统，开放系统能相容于新的、更高阶的结构（逻辑）法则建构，而趋向高层次相对完备――准完备。准完备只能在无限渐近进化（生长）过程中逐步取得，没有终点，只能是个趋向，我们把系统的这种特性，称为准完备性，相对于不完备性定理，可称其为准完备性定理。

系统遵循逻辑内涵与外延相容性定理，其参量可以无限内涵与外延，因而具有无限开放性，说明系统可从有序向更复杂有序演变。

③、逻辑层次的多元相容性

不同类型的参量在不同的逻辑层次上，构成不同类型的自组织结构，具有参量之间交互作用的唯一确定性，使每一种结构都即有相对独立性，又能相容于更大的系统，因而系统具有多元相容性。其低层次结构法则，总是要相容于高层次的结构法则而体现逻辑一致及相容性，其结构形式及互为因果性保持不变。这种特性体现了生物界及生物系统从简单有序到复杂有序的进化特征。其结构原理与法则，及参量的互为因果动力学特性的抽象描述，无疑是模拟复杂系统结构与功能的基本前提，也是自然科学理论要解决的根本任务。

④、参量有序及互为因果性

系统具有形式与内容、及结构法则的统一性。系统参量依据结构法则，在宏观上表现一致可构造性――自组织，体现出参量的有序及互为因果性。它保证系统在同环境的交互作用中，能实现自我维持、自我组织协调、自己创造（复制）自己。在内部协调、外部适应的基础上，能保证系统内耗最小、整体功能最优，系统行为或功能的预决性（即目的性）最强。

⑤、线性与非线性，连续与离散的统一性

任何一个整数加减任何一个整数，其结果必然还是一个整数，具可数可列性及加和性，因而属线性作用关系及系统。而有理数中的乘除、乘方开方对数反对数运算，具有可逆与不可逆的统一性，如1÷7＝0.142857, 具有不可逆、不可数可列及非加和性。但它相容整数群，说明系统可由简单向复杂进行相容演变――体现突变性。

至于连续性，一是指系统的参量可以无限微细化，可在任意精确度水平上进行模/数、数/模转换，一是指系统的建构及发展，是个无限的渐进过程。相对于离散性，连续性是系统演化的动态过程，离散性则是连续性的定态阶段化体现，没有离散性，就无法描述系统的特定结构――反映参量之间的交互作用关系，也表现不出准全息性，没有连续性，系统就不能表现出进化的自组织过程，两者具有统一性。

⑥、二值、多值与准多值逻辑的统一性

系统参量既可以是连续量，也可以是离散量，既可用二值表示，也可用二值的任意中间值表示，在现实世界中，多值、二值、及二值的任意中间值，其逻辑基础具统一相容性。

在客观现实中，只有准多值逻辑才能反映事物的本质特征，可相容各种逻辑功能，并具有辩证逻辑特性。可满足二值、多值及近似确定值、或近似隶属度的逻辑处理，从而既能描述及处理确定性问题，又能描述及处理非确定性问题，既所谓的模糊性问题，同时还能一致有效的描述及预测未知数。使因果确定性与几率的描述统一；使有限与无限、可逆与不可逆、对称与非对称的描述统一。只有在准多值逻辑的基础上，才能确定二值的任意中间值，这在二值逻辑中是难以想象的，二值只是准多值的特例。

模型还可体现皮亚杰有关结构主义的三个基本特性：

1、）整体性。

结构主义一开始便明确了这样一种对立关系，即结构与组成元素之间的对立关系，认为任何结构中各个部分不是孤立存在的，而且作为和其它部分的关系存在的。整体论的哲学分析方法并不拒绝对构成整体的部分的研究，认为整体与部分之间除了存在着对立外还存在着内在的统一性。整体的性质不是从整体外去寻找，而是由互相依存的各个部分的关系来说明。

2 、）转换性

结构中各个部分必须满足转换规则。根据这个规则，可以把结构某一部分转换成相应的另一部分。正是转换规则把部分连成整体，产生整体的性质。

3 、）自身的调整性

结构中各个部分存在着互相调节的能力。皮亚杰认为，调节有两个等级，有一些调节作用，仍然留在已经构成或差不多构造完成了的结构的内部，成为在平衡状态下完成导致结构自身调整的自身调节作用。另一些调节作用，却参与构造新的结构，把早先的一个或多个结构合并构成新结构，并把这些结构以在更大结构里的子系统的形式，整合在新结构里面。正是结构的这个要素使皮亚杰的结构主义具有建构的新特点。自身的调整性对结构是极为重要的，它即保证了结构作为整体的存在（相对确定的状态）又赋予了结构对环境的适应能力（不断完善自身的组织程度）。

皮亚杰以最典型的正负整数“群²”的结构说明了上述特性。其具体的逻辑表达式是：

n+0=0+n=n

n-n=-n+n=0

(n+m)+1=n+(m+1)

相对于系统描述及功能模拟，皮亚杰的结构主义还不能解决问题，因系统描述必须反应具体参量的普遍关系，而这种关系不能仅限于语言及公式描述，而一定要以某类参量的集合为基础，给出准全息元数学模型一样的结构描述，且必须是线性与非线性作用关系的统一；及决定论与概率论的统一，这样才能使系统科学象数学一样逻辑严密，或象物理学一样实在。

四、模型的意义

从智能机器的角度讲，其基础理论只能是一般系统论、控制论、信息论与自组织等自然科学基础理论的统一；是认识论、本体论、及方法论的统一。这是因为单纯靠哪一个理论都不能全面解决智能机器及智能模拟问题。模型相对于人脑是思维模型；相对于计算机则是计算模型；相对于系统论、信息论及控制论则是三论统一的定量形式化描述模型。

关于三论合一，钱老很早就提出并有过论述。三论统一的基础是同构，假设把系统参量看作一个集合，集合内参量的交互作用关系是系统的自组织自控制关系，这时集合的输出参量对等输入参量。两个相同集合之间则施控参量等价受控参量，这时我们就会发现系统参量等价施控与受控参量，如果把施控与受控参量看成是信息，则系统参量等价控制参量，同时等价信息单元。而信息的存储处理结构与施控与受控系统参量结构，从系统的角度看亦完全同构，这就是三论统一的基础。以往三论之所以分离，是因为各自的理论高度都难以统一其它两论，即不能从高层次给出统一定量形式化描述模型。

作为一个方法论，表明一个系统的结构，就是指出它的各个部分以及各个部分之间的相互作用关系。一个集合只作为集合来看是没有什么结构的，只有指出集合的内在逻辑结构模式，及与某个原型的同构性才有意义。同构概念相对于功能模拟具有重要意义，因产生功能的基础是结构，欲有效的模拟系统功能，就必须根据同构相似性原理有效的描述系统结构。

自组织是系统得以生存和演化的基础，是自然界物质、能量及信息互相作用、互相利用、互相调整的一种形式，自组织是自成体系的整体描述方法，可以帮助我们认识系统的内在规律和结构，进而利用这些规律解释可能发生的演变。因此，学习和掌握自组织原理及方法，就能有效的利用物质、能量及信息，使其发挥最大的效益。自组织问题，不仅是本体论、认识论问题，同时也是方法论问题。对自组织方法的掌握，有助于我们了解在什么情况及条件下，才能使得自然与社会资源有效利用与再生，亦有助于了解各种功能（包括智能）的产生机理。自组织方法就是自组织的定量形式化模型方法，据此，我们可以模拟特定的系统结构与功能。相对于最具复杂性的系统功能――人类智能，如没有定量形式化的自组织结构及原理，就谈不到有效的智能模拟，也不能说系统有了完善的理论基础。人类智能模拟的神秘化，及所遇到的困难，均与未能掌握这种原理与方法有关。根据模型的同构相似形原理，根据逻辑内涵与外延相容一致性原理，我们可以有条件的根据已知推出未知，根据底层结构推知高层结构，并有条件的进性有效模拟、把握及操控复杂的巨系统。

五、结束语

通过准全息元数学模型，系统论最起码不再限于定型描述，至于构成一个完备化的理论体系肯定还需要一个过程。复杂系统具有“‘进化”的特征，智能计算机的设计和开发只能以此为基础。系统理论、技术的不断发展将在涉及智能、生命和信息等前沿科学领域内，为人类探究自然及自身奥秘发挥巨大作用。

主要参考文献：

1、苗东升，系统科学辩证法，山东教育出版社，1998.12
       2、皮亚杰（瑞士）著，倪连生等译，结构主义，商务印书馆，1984.11
       3、王迪兴，准全息元数学模型－智能机的理论基础，全国首届智能机器人学术讨论会论文，1988.10（西安）。
      4、王迪兴，定量形式化的组织理论及人脑模型，思维科学通讯，92.1、2期合刊。
    5、王迪兴，“准全息元数学模型及其应用”，系统辩证学学报98(4)
    6、王迪兴，复杂适应系统的共性描述，系统辩证学学报2001（4）
    7、王迪兴，准全息论，第九届人工智能学术会论文集，2001、11、30（北京邮电大学）