注:本文OCR于《编辑学报》1999年8月11卷3期,135-139页,顺向作者和编辑部表示谢意。文中如有误,请以原文为准。本文是写给编辑的,但是对论文作者也很有帮助,故编入--编者。
----
回归曲线的审稿要领
![]()
张文举
关键词 回归曲线 数学模型
曲线方程
摘要 简述科技论文中回归曲线模型的初步选择方法;归纳总结17种常用数学模型的特点及其拟合方法,并绘制曲线示意图;指出曲线方程显著性检验的统计学方法。
科技论文中经常出现回归曲线,编辑人员在审读这类稿件时,特别要注意回归模型的选择、拟合方法及其显著性检验等方面的问题。本文就此作一归纳。
1.曲线回归的可行性判断
编辑在审读有回归曲线的稿件时,首先要判断作者拟合由线的目的是否明确,被研究的两个变量之间是否存在内在联系,对于那些毫无关系的数据拟合曲线的稿件,应当不予发表。因为这种曲线不仅未揭示事物的客观规律,而且极有可能掩盖事物的真实联系,从而误导读者。其次,要判断作者为进行曲线拟合而选择的回归模型是否合适。初步判断的依据就是看根据自变量和因变量的实际观察值绘制出的散点图曲线是否与该回归模型的曲线图形相似。如果相似,则说明此回归模型可能选择对了;否则,没有必要再对此稿件继续审读。
由于实验的结果总会受到抽样变动的影响,所以观察值的散点图与拟合曲线稍有出入的现象很难完全避免。有人用随手画成而通过所有观察点的“光滑”曲线代替拟合曲线,甚至据此进行推论或预测,这是很不妥当的,因为随手连接散点而成的曲线其走向不一定正确。
2.回归模型的特点
根据散点图曲线能否正确判断论文中回归模型的选择是否恰当,关键在于是否掌握常用回归模型的特点和图形。下面介绍17种回归模型的特点(见附图)[1-5]。
2.1 Y=a+bX
回归线为一条直线,它是一元曲线模型的特殊情况。当b>0时,Y
随X 增大而线性增大(图la);当b<0时,Y 随X
增大而线性减小(图lb)。直线与Y 轴的交点为(0,a)。
2.2 Y=aXb
当a>0, 0<b<l时,Y
单调递增且下凹,曲线过原点;当a>0,b>l时,y单调递增且上凹,曲线过原A,(图2a);当a>0,
b<0时,Y 随X 增大单调递减上凹,以X 轴和Y
轴为渐近线(图2b)。
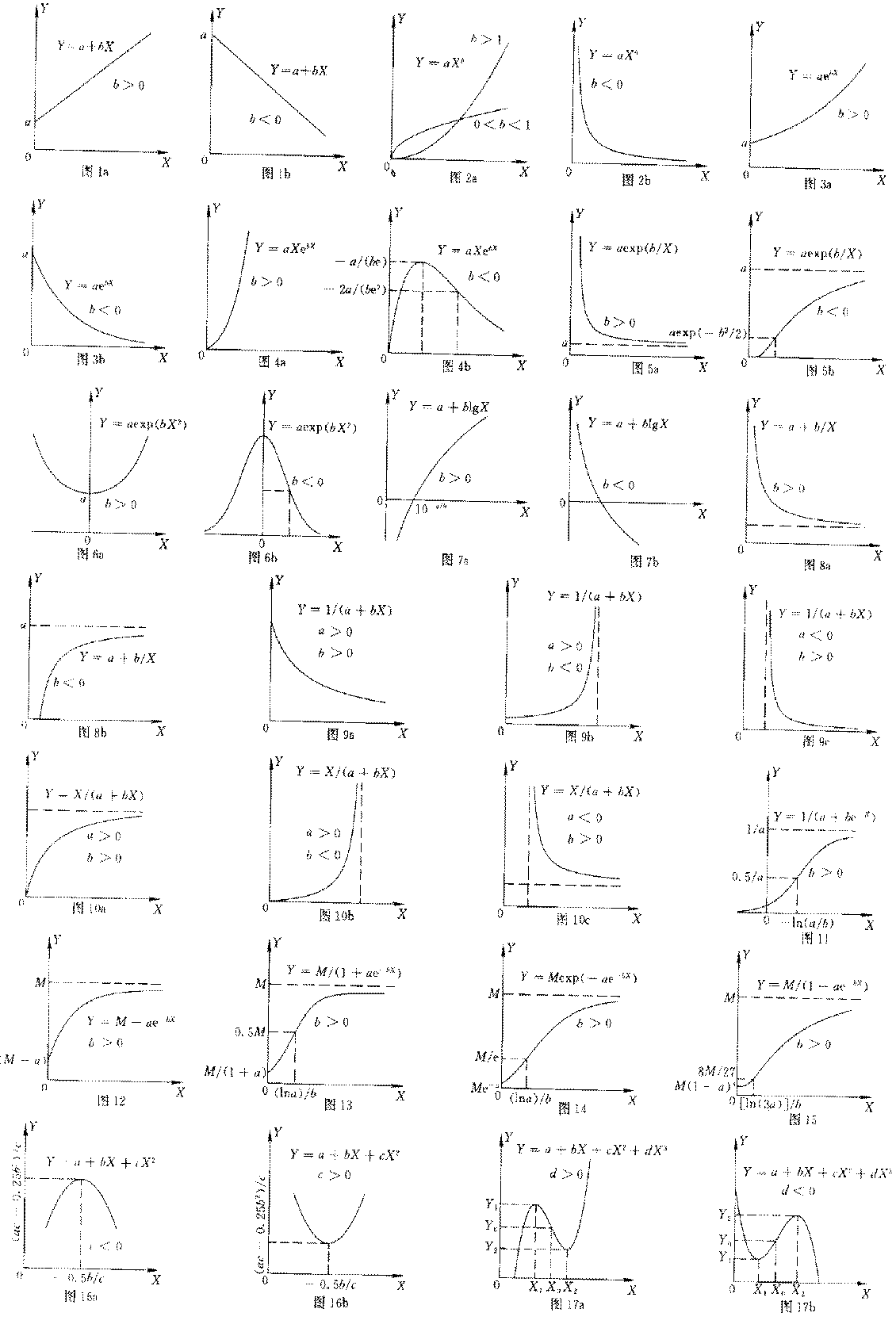
图1-17常用数学模型的示意曲线(图中未特别标注a<0者均为a>0)
2.3 Y=aebX
当a>0, b>0时,Y 随X 增大单调递增上凹(图3a);当a>0,
b<0时,Y 单调递减仍上凹,并向X 轴渐近。曲线与Y
轴的交点为(0,a)(图3b)。
2.4 Y=aXebX
当a>0, b>0时,Y 随X
增大而急速上升,曲线通过原点且上凹(图4a)。当a>0, b<0时,在X
的区间(0,-1/b)上,Y 单调递增,曲线通过原点;在X=-1/b时,Ymax=-a
/(be);在X 的区间(-1/b,+∞)上,Y
单调递减,其中,在区间(0,2/b)上,曲线下凹;在区间(-2/b,+∞)上,曲线上凹,向X
轴渐近;拐点坐标为X=-2/b,Y=-2a /(be2)(图4b)。
2.5 Y=aexp(b/X)
当a>0, b>0时,Y 随X 增大单调递减上凹,具有渐近线X=0和Y=a(图5a)。当a>0,b<0时,Y
单调递增;在X 的区间(0,-2/b)上,曲线上凹,且当X→0时,Y=0;X=-2/b,Y=aexp(-b2/2)为曲线拐点坐标;在X
的开区间(-2/b,+∞)上,曲线下凹,且以Y=a
为渐近线(图5b)。
2.6 Y=aexp(bX2)
此曲线关于Y轴对称。当a>0, b>0 时,有X=0,Ymim=a,曲线上凹(图6a),当a>0,
b<0时,有极大点(0,a);点X=(-0.5/b)0.5,Y=a/e0.5和X=-(-0.5/b)0.5,Y=a/e0.5为曲线的两个拐点(图6b)。
2. 7 Y=a+blgX
当b>0时,Y 随X 增大单调递增(图7a);当b<0时,Y单调递减。曲线与X轴的交点坐标为(10-a/b,0)(图7b)。
2.8 Y=a+b/X
当a>0, b>0时,曲线有渐近线X=0 和Y=a,Y
随X 增大单调递减,且曲线上凹(图8a);当a>0,b<0时,Y单调递增,且曲线下凹,曲线与X轴的交点坐标为(-b/a,0)(图8b)。
2.9 Y=1/(a+bX)
曲线上凹。当a>0, b>0时,Y 随X
增大单调递减,以X 轴为渐近线,曲线与Y
轴的交点为(0,1/a)(图9a);当a>0, b<0时Y
单调递增,以X=-a/b为渐近线,曲线与Y
轴的交点坐标为(0, 1/a)(图9b);当a<0, b>0时,Y
单调递减,以Y=0和Y=-a/b为渐近线(图9c)。
2.10 Y=X/(a+bX)
当a>0, b>0时,曲线通过原点,Y 随X
增大单调递增,向Y=1/b 渐近,曲线下凹(图10a);当a>0,b<0时,曲线通过原点,Y
随X 增大单调递增且向X=-a/b
渐近,曲线上凹(图10b);当a<0,b>0时,在X
的区间(-a/b,+∞)上Y
取正值,且单调递减,曲线上凹,具有渐近线X=-a/b和y=1/b(图10c)。
2.11 Y=1/(a+be-X)
当a,b均大于零时,有水平渐近线Y=O和Y=1/a;拐点坐标为X=-ln(a/b),y=0.5/a(图11)。
2.12 Y=M-ae-bX
为Mitscherlich 增长曲线,M,a,b均大于零。Y 随X
增大单调递增,且上凸。当X=O时,Y=M-a;X→+∞时,Y=M(图12)。
2.13 Y=M/(l+ae-bX)
为Logistic增长曲线,M,a,b均大于零。当X→+∞时,Y=M
。拐点坐标为X=(Ina)/b,Y=0.5M
。拐点之前曲线上凹,拐点之后曲线下凹。当X=0时,Y=M/(1+a)(图13)。
2.14 Y=Mexp(-ae-bX)
称为Gompertz增长曲线,M ,a,b均大于零。拐点坐标为X=(Ina)/b,Y=M/e,拐点之前曲线上凹,拐点之后曲线下凹。当X→+∞
时,Y=M;当X=0时,Y=Me-a(图14)。
2.15 Y=M(1-ae-bX)3
称BertallanffY增长曲线,M,a,b均大于零。拐点坐标为X=[ln(3a)]/b,Y=8M/27。拐点左侧曲线上凹,拐点右侧曲线下凹。当X→+∞时,Y=M;当X=O时,Y=M(1-a)3(图15)。
2.16 Y=a+bX+cX2
称为二次抛物线。a 是曲线与Y 轴交点之纵坐标。当c<0时,曲线有一个极大点,曲线两端斜向下方延伸(图16a);当c>0时,曲线有一个极小点,两端斜向上方延伸。极点坐标为X=-0.5b/c,Y=(ac-0.25b2)/c(图16b)。曲线两端相距的广狭程度则视系数b和c的数值而定。
2.17 Y=a+bX+cX2十dX3
这是三次抛物线。当d>0时曲线呈“N”型(图17a),当d<
0时呈“и”型(图17b);通常有极大点、极小点和拐点各一个,d值大于零和小于零时极大点和极小点的先后顺序相反。
将X0=-c/(3d)代入Y0=a+bX+cX2十dX3
可得拐点坐标(X0,Y0)。
如果三次抛物线有极点,则令3dX2+2cX+b=0可求得此一元二次方程的两个解X1
和X2 ,将X1 和X2
分别代入三次抛物线方程可求得两个极值Y1 和Y2
。
如果三次抛物线的图形中只有拐点而无极大点或极小点,便是所谓的“消退型”曲线。医学资料中有些是适于消退型曲线的,它表示Y 值始终随X 的增大而增大或y 值始终随X 值的增大而变小,虽然增大或变小的速度并不一致。
3.曲线方程的拟合方法
选择了适当的曲线模型之后,就必须采用正确的方法去拟合曲线方程。实际上就是根据实际观察值(X1,X2,...Xn
; Y1,Y2,…Yn)和观测次数n,计算出数学模型中的系数a,b,c,d
等。
3.1 一元直线方程
一元直线方程作为曲线方程的特殊情况在曲线方程的拟合中具有相当重要的作用,作者和编辑应予以掌握。
对于数学模型Y=a+bX来说,只要求出下列一组正规方程中的未知数a和b便可拟合出一元直线方程Y=a+bX:
aN+b∑X=∑y
a∑x+b∑x2=∑XY
3.2 可化为一元直线模型的曲线方程
如附表所示,前述数学模型中,除两个抛物线模型之外的其他14种模型都可化为直线模型,并按照3.1的方法拟合相应的曲线方程。当然模型转化之后,原始数据也要作相应的转化。
| 数学模型 | 转化方法 | 转化后形式 |
| Y=aXb | U=lgY,V=lgX,A=lga | U=A+bV |
| Y=aebx | U=lnY,A=lna | U=A+bV |
| Y=aXebx | U=ln(Y/X),A=lna | U=A+bV |
| Y=aexp(b/X) | U=lnY,V=1/X,A=lna | U=A+bV |
| Y=aexp(bX2) | U=lnY,V=X2,A=lna | U=A+bV |
| Y=a+blgX | V=lgX | Y=A+bV |
| Y=a+b/X | V=1/X | Y=A+bV |
| Y=1/(a+bX) | U=1/Y | U=A+bV |
| Y=X/(a+bX) | U=1/Y,V=1/X | U=A+bV |
| Y=1/(a+be-x) | U=1/Y,V=e-X | U=A+bV |
| Y=M-ae-bX | U=ln(M-Y),V=-X,A=lna | U=A+bV |
| Y=M/(1+ae-bX) | U=ln(M-Y)/Y,V=-X,A=lna | U=A+bV |
| Y=Mexp(-ae-bX) | U=ln[-ln(Y/M)],V=-X,A=lna | U=A+bV |
| Y=M(1-ae-bX)3 | U=ln[1-(Y/M)1/3,V=-X,A=lna | U=A+bV |
3.3 二次抛物线方程
二次抛物线模型Y=a+bX+cX2中有三个系数,只要解出下列一组正规方程中的未知数a,b,和c,则可拟合出二次抛物线方程Y=a+bX+cX2:
aN+b∑X+c∑X2=∑y
a∑X+b∑X2+c∑X3=∑XY
a∑X2+b∑X3+c∑X4=∑X2Y
3.4 三次抛物线方程
三次抛物线模型Y=a+bX+cX2+dX4
中有四个系数,与二次抛物线模型相似,只要解出下列一组正规方程中的未知数a,b,c,d
便可拟合出三次抛物线Y=a+bX+cX2+dX4:
aN+b∑X+c∑X2+d∑X3=∑y
a∑X+b∑X2+c∑X3+d∑X4=∑XY
a∑X2+b∑X3+c∑X4+d∑X5=∑X2Y
a∑X3+b∑X4+c∑X5+d∑X6=∑X3Y
上述简捷方法拟合的回归曲线,还可采用逐步近似法进行校正。校正方法比较繁琐,实践中又不大常用,这里就不再赘述了。
4.曲线方程的显著性判断
检验的目的有两个:一是检查所配曲线是否比较适合,例如二次抛物线是否比直线为优,或指数是否比二次曲线为优,等等;二是检查所配曲线能否代表原始资料各观察点的趋势。也就是说,此类稿件中应当阐明曲线的显著性检验。否则,读者会怀疑曲线的意义和拟合效果。检验方法通常有F检验和t检验。
参考文献
1 袁志发,顾天骥,主编。概率基础与数理统计。北京:农业出版社,
1988.221-237.
2 俞渭江,主编。生物统计:附试验设计,北京:农业出版社,1980.
114-130.
3 张文举,徽成盆地黄牛生长曲线方程的研究。甘肃畜牧兽医。1998,28(1):3-6.
4 郭祖超,编。医用数理统计方法。北京:人民卫生出版社,1963.414-458.
5 符伍儒,主编,数理统计,北京:农业出版社, 1980.223一234.
----
张文举,男,35岁,农学硕士,主任,副主编,《甘肃畜牧兽医》编辑部,
744000甘肃省平凉市崆峒东路143号
收稿日期: 1998-07一22,修回日期:1999-05一15