重力场中热力学的研究（9）

第五章 对几个具体问题的讨论（2）

三. 第二类热机

所谓第二类热机，即借助力场效应(最终等效于)将热能100%地转化为非热能的装置。示例如下：

图2

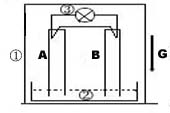
图2中，在一真空绝热罩内①(处于重力场中)，有两根相同高度铅直放置的管(不导热)，A管内充满氦气，B管内充满氡气，两管下端开口均浸在水银槽中②，上端口内分别设置温差电偶(密封)，外部用导线连成闭合回路，在导线中串接一只灯泡③。

根据重力场中的温度梯度公式()，图2中，由于g不变、高度h相等, , 又两管下端插在同一液槽中，则温度相等，T_0,He-T_0,Rn=0，其上端温差为： 因即：T _He＞T _Rn, 这表明两气柱上端有稳恒的温差，如果气柱高度均为500m，两气柱上端温差为36.83K。温差电路将产生电流使灯泡发光，这时氦柱上端电极将耗热欲使气温下降，而氡柱上端电极将生热欲使气温上升, 而场力(比势焓平衡规律) 竭力维持气柱额定的温差，使氡柱上端热量向下端转移, 氦柱下端热量向上端转移，以维持其温差(即比势焓平衡), 设这两气柱的横截面积足够大, 以保证其温度的稳定.最终以消耗水银的内能为唯一代价转换成当量的电能, 虽然热电偶一次转换效率很低, 但通过多次的热量循环, 其最终效果相当于该热电转换效率达100%。尽管它一时还未显示出实用价值，但它从原则上超出了热力学第二定律的开尔文表述。

这里不妨详尽指出，两柱的热流是不相等的，因为J_qA=ε_AI_A, J_qB =ε_BI_B, 而I_A=I_B, 因为属无支流电路, 而ε_A≠ε_B，因为T_A≠T_B，又ε=f(T), 故J_qA≠J_qB 。

笔者的目的不是想发明永动机, 尽管上例从理论上讲是可以的, 但由于地球的重力场g值太小, 使人们无法造出有实用价值的机器来, 但笔者认为宇宙中的恒星具有永动机的性质。

四.负的熵密度产生率

熵密度产生率与热流的关系式^[1]为

, (1)

(1) 式中,d_is°/dt表示只存在热流而(2) 无物质流时所导致的局域熵密度的产率,

s°为比熵(即局域的熵与局域的质量之比) ，J_q称为热流密度，▽ (1/ T) 称

为热流动力，对于匀强力场，, ▽=d/dh, 其dh为沿场力线的位移增

量, 将 (见第六章),用J_qh替代J_q代入(1) 式得

=

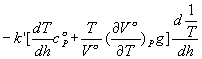= , (2)

(2)式中, 设(通常为正数) ，

(2)式简写为 (3)

对(2)式进行分析如下

1、在无重力场(g=0)或在等势面(dh=0)上, 即B =0时,

(2)式变为其值永不小于零，当有温度梯度时[(dT/dh)≠0]，热量自动地由高温区流向低温区，这种仅由温差产生的热流引起的熵产生永远大于零，这是传统的熵增原理描述的情形。

2、在重力线上

当(dT/dh)＞0(温度依高度递增，温度梯度与势函梯度方向一致) 时 ，即

A＞0, B＞0, C＞0。

由(3)式可知：(d_is°/dt)＞0，热量自动地由高比势焓区向低比势焓区转移, 此为不可逆过程。

当(dT/dh)=0(温度分布均匀) 时，即A =0, B＞0, C =0,

由(3)式可知：(d_is/dt)=0，热量必将自动地由高比势焓区向低比势焓区转移，但这已属不可逆过程, 这已不能用传统的熵增原理来理解了。

当(d T/dh)＜0(温度依高度递减)时，若｜A｜＞｜B｜, A＜0,B＞0, 必 A+B＜0, 又 C＜0,

由(3)式可知： (d_is°/dt)＞0；若｜A｜=｜B｜, A＜0, B＞0, 必 A+B=0, 又C＜0,所以(d_is/dt)=0，体系无热温商的变化, 因为这时体系处于比势焓平衡状态, 即无热流产生处于全面“静止”的状态。

总之,凡沿场力线进行热传导的过程均不服从传统的熵增原理, 其可逆过程的熵变已不再是零值。

特别情形是：在力场中,当｜A｜＜｜B｜, A＜0, B＞0, 则A+B＞0, 且C＜0, 由(3)式可知：(d_is°/dt)＜0。

这是热量由低温 (高比势焓) 区传导至高温 (低比势焓) 区的过程，这时显然与熵增原理不相容, 因为熵增原理要求任何热流过程的熵密产生率永不小于零，热力学第二定律中的克劳修斯表述说明,无论如何不可能出现热量自动地由低温区传导至高温区的现象(即反克劳修斯过程)，上述分析表明熵增原理的适用范围是有局限性的(仅适用于同一等势面上)，克劳修斯表述是要修正的,即主导热力学体系的是比势焓平衡趋势而不是传统的熵增原理。

参考文献

[1] 汪志诚 1993 热力学·统计物理(中国 高等教育出版社) 185