重力场中热力学的研究（8）

第五章 对几个具体问题的讨论（1）

一.关于净熵减的讨论

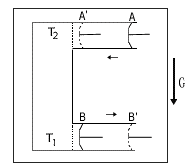图1

图1装置与外界绝热(熵孤立系统)，上下两气缸内均可容有一摩尔理想气体，竖直柱内盛满液体，气缸与液柱接触处由导热的板隔开(不能穿过物质)，液柱处于稳恒态，依据比势焓平衡规律(见第六章)的推论，液体内存在着上低下高的温度梯度，即T₂＜T₁，上气缸内气体温度与液柱上端温度(T₂)相同，下气缸内气体温度与液柱下端温度(T₁)相同, 上气缸初状态(A)气体体积V₂温度T₂, 终状态

(A′)气体体积V₂′温度T₂′,下气缸初状态(B)气体体积V₁温度T₁, 终状态(B′)气体体积V₁′温度T₁′ 。令两活塞按图示方向作绝热准静无摩擦的可逆位移，上活塞等温(T₂=T₂′)压缩气体，同时下活塞在气体等温(T₁=T₁′)膨胀下退出。

由于活塞作准静态变化，而活塞的准静态移动不能破坏液柱的稳恒态,故液

柱内各点的温度、密度不变，当然液柱的总内能也一直不变, 其熵也

一直不变^[1] 。而上下两缸均作等温可逆的体积变化, 故上下两缸中理想气体各自所拥有的内能一直不变。这就表明上缸气体吸收的外功等于下缸气体

释放的体积功。即在Q=ΔU_总 +W中,Q=0(绝热) ，ΔU_总=0，故W=0，

则 ,或 , (1)

,,

即 ,

或<0, (2)

因T₁=T₁′, T₂=T₂′ , 而理想气体的熵表达式为s=RlnV+C_VlnT ，故而可知

, 为上下两缸中气体始终态的熵变值，其值小于零，

而与之耦合的液柱的总熵 一直不变 ，这是绝热系统内总熵减少的情形。

上述情形也可从热量转移方面来分析，上气缸释放出的热量 从液柱上端向下端准静态转移，全部被下气缸吸收由(1) 式可知｜Q₁｜=｜Q₂｜= Q,其热温商由｜Q₂｜/T₂ (上气缸熵差)变为｜Q₁｜/T₁(下气缸熵差),而T₂＜T₁, 故(｜Q₂｜/T₂)＞(｜Q₁｜/T₁)或(｜Q₁｜/T₁)-(｜Q₂｜/T₂) ＜0, 即热量由低温处向高温处等量转移是热温商递减的过程，这超越了熵增原理中克劳

修斯表述的范围, 因为此例之外谁也未曾找到过绝热系统熵净减少的例子。

注释

[1].因图(1)中的液柱A′B部分无热源, 即有▽·J_q=0, 同时流过液柱各个截面的热量始终是相等的, 即有,因为,又因, 故有。而故有,或。

另一种思路是:, 其中仍表示液柱某点的熵密度改变率, 则表示因熵流()引起的熵密改变率, 而则表示由热流所导致的熵密产生率, 因其熵密改变率无外乎由这两种因素所致, 由立即可知, 与这两项要么同时为零, 要么保持一对相反数.总之只要无热源永远不会导致不等于零的熵密改变率, 故永远有。

这里用两种逻辑思路殊途同证该液柱的熵为恒定值。

二. 熵减的统计解释^[1]

上述关于图1所示过程的熵变分析是从热学角度进行的, 这里再从经典统计的思路进行再讨论。

由于图1中的竖直段液柱为稳恒态, 故其微观状态数一直保持不变。对于图1装置中的活塞移动(绝热可逆过程), 上、下两气缸中的初、终态微观状态总数会怎样变化呢？

由上一节(2) 式可知,

即： 或, (1)

(1) 式中nk=R,k为波尔兹曼常数,n为粒子数。

即 (V₁′ V₂′) ⁿ - (V ₁V₂)ⁿ ＜0, (2)

由于V与Ω成正比, 即Ω=(1/ ho)³V, 令(ho)³为体积元胞, ho为某极小极小的正数。

所以

故 Ω_V ′-Ω_V＜0, (3)

(3) 式中,Ω_V和Ω_V ′分别表示系统初态与终态时两气缸中所有分子在空间各点的分布的所有可能的方式总数,(3) 式表示终态比初态(两气缸中理想气体各分子) 可取的微观状态总数减少了！这是传统的熵增原理的违例, 因为传统的熵增原理要求任何绝热过程其体系内的微观状态数总不会减少(即混乱度总不会降低) 。但这并不意味着麦克斯韦妖的存在, 即并不意味着气体可以自动收缩, 或曰引力及其它什么因素都不能使气体在绝热收缩时而不伴随温度变化的所谓流体的单纯体收缩, 只能发生单纯体膨胀，如理想气体单纯的绝热自由扩散，但不可能发生混合流体的自动(单纯) 分离而净化的过程。

参考文献

[1] 张三慧等 1991 热学(清华大学出版社) 158