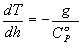重力场中热力学的研究（6）

第四章 处于重力场中的平衡态体系内

存在着稳恒的温度梯度

  二. 用“绝热稳定流能量方程” 导出温度梯度关系式

本文从《流体力学》教材中“绝热稳定流能量方程”出发，导出了“力场中绝热平静的理想气体内存在着稳恒的温度梯度,且不会导致传导热流产生” 的认识。

1 引言

过去，前人依据热力学第一定律结合稳流特征推得“绝热稳定流能量方程”, 在《流体力学》中对该方程仅讨论了当流体沿等势面流动(比势能为常数)的情形, 且得到所谓“喷射方程” ，而本文只感兴趣讨论流体作匀速运动或静止状态(比动能为常数)的情形，由此试图证明引力可导致绝热流体内存在着永恒的温度梯度。

2 “绝热稳定流能量方程” 及其讨论

对于均匀系统，其焓为

H=PV+U (1)

(1) 式中,H表示一摩尔流体拥有的焓,P表示系统的压力,V表示一摩尔流体在压力恒为P时所占有的体积, U表示一摩尔流体所拥有的内能。

而对于非均匀系统，上述焓及其它广延参量就都不适用了, 但可使用“比焓”概念，其定义式为：

H°=(H/m)=P(V/m)+U/m=PV°+U° (2)

(2)式中, H°为单位质量的焓, 此称“比焓”, 其单位为kJ/kg , m为一摩尔流质的质量,PV°称为“比流动功”, V°(V/m) 即为“比容”,U°(U/m)称为“比内能”, 这些强度参量在点函数中都具有确切的物理内涵。

同理, C_P°(C_P/m) 表示“等压比热”, C_P为摩尔热容。R°(R/m)表示某种气体“比常数”, 在下述讨论中运用了上述符号。

《流体力学》中给出了“绝热稳定流能量方程”

H°+(1/2)v²+gh=常数 (3)

(3)式中, H°为比焓,v为流体质元的流动速度,g为场力加速度, h是流体质元(可视为质点)到指定参考面的高度。(1/2)v²为流体质元的“比宏观动能”，gh为其在外场中的“比势能”。

当流体作匀速^[1]或准静态流动或静止状态时,其比动能项为一常数或逼近于零或等于零 ，这时(3)式变为

H°+gh=常数 (4)

其实(4)式也就是一切流体的静力学方程，它既适用于不可压缩流体(U°=常数), 也适用于可压缩流体(U°≠常数) 。

3 理想气体流体的静力学方程的热力学表达式

理想气体的比焓可表示为“C_P°T”, 即有下列关系式^[2]

H°= C_P°T (5)

将(5) 式代入(4)式得

C_P°T+gh=常数 (6)

(6)式就是理想气体静力学方程的热力学表达式。式中, 等压比热C_P°和力场加速度g都是不变量,只有参考高度h为自变量, 故体系各点温度T必为h的函变量, 这表明在力场中绝热平静的理想气体内各点温度是依其参考高度h而定的。

4 温度梯度公式

(1) 理想气体内存在温度梯度表达式的导出

由(6)式可得

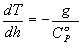(≠0) (7)

(7)式就是温度梯度表达式, 式中清楚地反映了在匀强力场中绝热平静(终极状态)的理想气体内存在着永恒的温度梯度，负号表明其温度分布是依其参考高度h递减的, 它描述的这种温度梯度是由力场导致的,即为“广义平衡态”(势焓平衡),与热源无关,这里当然不存在传导热流^[3] , 即无熵流伴随、无熵产生, 即为定熵状态。(7)式也说明, 只有在无力场空间(g=0) 或同一等势面上(dh=0)的各点温度才处处相等(dT=0)。

(2)一般流体内存在温度梯度表达式的导出

由?/FONT>比势焓平衡方程?/FONT>(▽H°+g=0或H°+gh=常数) 得

故得 (8)

(由静力平衡关系, 即dP+ρgdh=0变形得)]

(8)式即为一般流体内(匀强力场中)存在温度梯度表达式, 它表明在力场作用下的绝热静态流体内客观地存在着稳恒的温度梯度。它揭示出静态流体的温度分布总要叠加一个稳恒的温度梯度。为流质在压力恒为P时比容的相对膨胀率，它的值通常大于

零(注意V°ρ=1)。

当流体为理想气体或稀薄气体时, 依有

则 (8)式变为

若写成差分形式则为 , (9)

(9)式是理想气体在匀强重力场中的温度梯度关系式，这与《气象学》中的绝热气温直减率相雷同(即干空气块绝热准静可逆地每垂直上升100米其温度的减少值) 。(9)式中, ΔT是流质在场力线上某两点之间的温度差，负号表明温度分

布依高度递减,g是重力加速度, Δh是某两点之间的高度差，c_P°是等压比热,如单原子理想气体: c _P°=(5/2)R°,双原子分子理想气体：c_P°=(7/2)R°，R°为普适气体比常数，R°=8.3/m(焦耳/度·摩尔·千克),m为相应气体的摩尔质量.

唯象讨论示例：在地球表面,100米高度的绝热空气柱上下两端温度差是多少[空气平均摩尔质量为28.9克, g取9.8米/秒²,C_P°取(7/2)R°]？

解: =

地球表层实际大气每百米高度平均温差为-0.65K，因地球大气不是绝热静态系统，还叠加着其它因素导致的温度梯度,故温差实际值与理论值有一定差距。这里不仅仅是反映了温度梯度的事实，更主要是揭示温度梯度的成因本质及其永恒性，即力场效应(而不是全由热源因素造成的) 。

另外, “绝热稳定流能量方程”也可由“均熵方程”导出^[4] , 这充分说明第一、二种导出方案是相通的。

参阅资料

[1]由于流体密度梯度为(dρ/dh)≠0,当横截面积与其密度乘积为常数(ρS=常数) 时，即可保证其作匀速流动。

[2]邱信立等编《工程热力学》中国建筑工业出版社 1992年10月第三版 P.154

[3]绝热平静的流体内无传导热流的理论证明

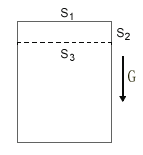
图1

图1表示绝热的园柱形容器(主视图)内容平静的流体, 处于重力场中, 该流体的上部“微元”(薄层)由上底S₁、侧面S₂、下底(虚线)S₃围成。

图1装置中, 当流体处在静态时, 该体系必属一种稳恒态，故必有,即各点温度与时间无关, 亦即有

(10)

(10) 式中，ρ为流质的密度,dV为微元体积, C′为其比热(其值还与具体过程有关, 对于稳恒态则为等容过程), 表示由热流所引起的某微元对热量的蓄积率。另外，当热力学第一定律作用于微元，则有δq=du+pdV,

 或，因是稳恒态，故有 必有。

依热流连续性方程

依积分变换

对于该微元可表示为 (11)

(11) 式中,S₁+S₂+ S₃ =S, 因S₁、S₂均为绝热壁, 故J_q1 =0, J_q2 =0, 因零的定积分为零, 即 必有 故J_q3=0(因S₃极小, 故穿过截面S₃上各点的热流近乎相等，更不可能出现互为异号, 即 因S₃≠0, 故J_q3=0) 。

上述分析表明无热流穿过S₃截面, 依此可递次推证(图示中以下)各层面均无热流穿过, 即绝热静态流体中虽然存在着永恒的温度梯度, 却无传导热流依存，故此为无熵流的“广义平衡态(势焓平衡) ”。

[4] ?/FONT>比势焓平衡方程?/FONT>(H°+gh=常数)的导出

因为有▽H°=T▽s?V〃孭 (12)

在(12)式两边同时加上一个相同的量得

▽H°+g=T▽s?V〃孭+g (13)

而▽s?0(均熵方程), 又▽P+ρg=0(静力平衡条件),ρV?1, 故有V〃孭+g=0

将其代入(13) 式即得?/FONT>比势焓平衡方程?/P>

▽H°+g=0或H°+gh=常数 (14)

其实(14) 式也就是可压缩流体的静力学方程,H°为比焓,gh为比势能,h为某点的参考高度。