说明:物理学的熵联系着统计力学。玻尔兹曼创立的统计力学不仅在物理学中取得了成功。它在其他领域也有用武之地。我们主张把它的核心思想准确地用到一切可能应用的领域去。下面这一篇文章就是把它用于气象学的降水问题的事例。它或许对大家是个启发。
编者
![]()
降水统计力学简介(1)
张学文
(新疆气象科学研究所,830002)
提要
我们曾经在1981年把统计物理学中的玻尔兹曼统计方法移植到气象学中的降水研究,这为认识降水现象提出了新思路,并且提出了“降水统计力学”一词。本文把这些年来本领域的进展做简要综合介绍。本部分(1)介绍有关概念和原理,(2)介绍应用实例等内容。
关键词:降水,统计力学
1简述
“降水统计力学”一词来自1981年《新疆气象》杂志三篇文章[1,2,3]的副标题。后来一些同志又发表有关文章约20篇,这里对它做简要介绍。
降水统计力学不同于一般的降水统计计算分析也不同于动力学的降水模型。它把统计(物理)力学中的思路用于分析降水现象,配合一些合理的假设得到了一批描述降水现象的定量的理论公式。这些公式从降水的历时、面积、深度等多侧面揭示了降水的统一的规律性。这些理论公式不是仅适用于某一个地点的经验方程,而是有普遍型(普适性)。它把气象上很困难、应用上很重要的降水问题中的未知数减少了很多。降水统计力学提供了一组关于降水的有理论有验证有实用图表的新知识。
2.用分布函数描述降水问题
降水统计力学利用分布函数[4,5]描述降水问题;用统计力学中的玻尔兹曼统计分布[6,7]寻找理论答案。本节介绍分布函数。
2.1分布函数概念
我们常说“年龄在人口中的分布、雨量在地域上的分布、财富在人群中的分布…”,“分布”一词是定性地描述事物内部结构的。现在介绍的分布函数概念则用函数描述分布,它使分布问题的答案定量化了。
例如不同的年龄的中国人关于各有多少?其答案就是年龄在人口中的分布函数。表(1)是它的概念化的表。
表(1)不同年龄的人各有多少
年龄段 |
10以下 | 10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
60-70 |
70-80 |
80以上 |
人口数 |
n1 |
n2 |
n3 |
n4 |
n5 |
n6 |
n7 |
n8 |
n9 |
一场暴雨落到了100万平方公里的面积上。根据雨量资料可以绘出一张雨量在地域上的分布图。利用这张图可以统计出如下的表:
表(2)一场暴雨的雨量在面积上的分布关系(示意)
雨量 |
小于20mm | 20-40mm |
40-60mm |
60-80mm |
80-100mm |
大于100mm |
面积 |
50 |
25 |
13 |
6 |
3 |
3 |
这个表给出了面积与雨量的对应关系。如果把第一行的雨量看成一个自变量x 的各种值而把第二行看成该雨量对应的面积值(因变量y),从数学上看即y 是x的函数。因为x与y的对应关系概括了雨量在面积上的分布,称它为分布函数。表(3)是概念化的分布函数。
特征值 |
x1 |
x2 |
x3 |
… |
xi |
… |
xk |
个体数 |
y1 |
y2 |
y3 |
… |
yi |
… |
yk |
上面的讨论表明:
1.分布函数概括一个系统的内部情况,这个系统由很多个个体组成的。在人口的例子中个体指的是每个人,在降水的例子中,个体指的是每1平方公里的雨区面积。 2.对于每个个体都有一个明确的特征值。每个人都有个明确的年龄,雨区里的每平方公里面积都有个明确的降水量。 3.分布函数给出了不同的特征值的个体各有多少。综上所述,
当把一个总体(系统、体系)恰当地看成是由多个地位相同的个体组成时,如果每个个体对某种特征(标志)都有明确但不尽相同的特征值(标志值)时,统计出不同特征值的个体各有多少,那么特征值与个体数量的关系就称为这个系统的分布函数。
2.2降水分布函数个例明确了分布函数概念后,可以把很多降水问题表示为求一个对应的分布函数问题。除了前述雨量在面积上的分布问题外,这里再举四例。
2.2.1单点的一场降水的强度分布函数 一场降水过程中有时雨急有时则慢[8]。把当地的一次降水过程的历时T (如18小时)看成一个总体(系统),而把每5分钟看成是一个个体(18小时含216个个体)。如果有降水自记记录,就可以从自记纸上读取每5分钟的降水强度。从而得到示意表(4)表(4)对降水自记记录的初步整理表
| 以5分钟为单位的各个时段 | t1 |
t2 |
t1 |
t1 |
t5 |
t6 |
t7 |
… |
ti |
… |
t216 |
| 该时段降水量r | r1 |
r2 |
r3 |
r4 |
r5 |
r6 |
r7 |
ri |
… |
r216 |
表(4)中每个时段的长度都相同(5分钟),而每5分钟内的降水量(应当称为降水强度了)不可能都相同。即r1,r2,r3,… ,r216 等等可能有相等的也会有不相等的。如果把降水强度从小到大分成6个档次,再从这个表中统计出不同降水强度的降水共计维持了多少个时段,就得出表(5)
表(5)从降水自记统计出来的不同强度的 降水的维持时间各有多少(n1,n2…)
降水强度的档次 |
1档 |
2档 |
3档 |
4档 |
5档 |
6档 |
该强度的降水共维持了几个时段 |
n1 |
n2 |
n3 |
n4 |
n5 |
n6 |
表(5)符合分布函数所要求的数据格式,它实际就是关于一场降水过程中降水强度的分布函数。
2.2.2单点的过程雨量的分布函数
天气学可以划分出一次次的降水过程来。考虑某地的每次降水过程都有一个具体的降水量,就可以研究不同的过程降水量的出现的机会的大小问题。这就是单点的过程雨量的频率分布问题[1]。有足够的资料,可以得到一个稳定的频率分布函数。
我们曾经证明[4,5]频(概)率分布与这里介绍的分布函数是等价的问题。所以过去的统计气象中的这类问题也可以归入我们的降水统计力学中。即单点的过程雨量的频(概)率分布也是一种分布函数。
在具体研究中考虑到有些地区、有些季节一场雨难得超过24小时。这可以用24小时降水量粗略代表一次降水过程的雨量。如果一个地方在某个季节有多年的降水资料,就可以统计出当地不同雨量的降水过程各有多少次。这就可得到不同的24小时雨量与出现次数(概率)的关系。它就是单点的过程雨量的分布函数的近似关系[9]。
2.2.3单点的降水历时分布函数
气象观测规定降水间歇了15分钟就是两个降水过程了。据此从气象资料中就可以得到每场雨究竟下了长的时间。在多年的(同一季节)降水资料面前我们就提出了不同的降水历时的降水各出现多少的次的问题[10]。显然,当资料样本很多时我们会统计出当地的不同的降水历时各有多少次的。把每次降水过程看成一个个体,把每次降水的维持时间看成它的特征值(标志值)。不同的维持时间与出现次数的关系就符合分布函数的含义,所以这实际上是一种关于降水历时的分布函数。它用一个函数描述了当地的降水特点。
2.2.4单点的干旱期长度的分布函数
两次降水过程之间的无雨期也称为干旱期[11]。干旱期有长有短,在充分多的气象资料面前我们可以统计出当地的不同的干旱期长度各有多少次,这又是个函数关系。把每个干旱期当做一个个体,把干旱期的长度当成标志值(特征值),那么不同标志值与不同的个体数量的关系就是一个特定的函数关系,这个关系就是关于干旱期的分布函数,它用一个函数描述了当地的又一种气候特点。
上面的四个例子和最初的雨量在面积上的分布都是分布函数概念在降水问题的应用。在后面的应用实例部分我们要给出更多的例子。现在转而研究形成这些分布函数(现象)的原因。
3.玻尔兹曼分布
上世纪麦克斯威把分布函数概念用于分子运动而玻尔兹曼求得分子动能的最可几的能量分布,这被称为玻尔兹曼分布[6,7]。我们把他的思路从微观的分子尺度移到气象尺度,把分子“能量”移植到气象上“雨量”等气象变量上。由此得到了若干与事实一致的降水的最可几的分布函数。由于这个原理与气象上的降水实践相符,统计力学的原理也就在气象领域有了立足之地。现以降水的面积分布问题为例简述之[3,12]。
3.1基本思路
大气中发生了一次降水过程,它把体积为V的雨水降落到面积为A的地面上。其平均雨量![]() 应当是
应当是
![]()
如果降水过程把雨水均匀地洒先向地面每个地方得到的雨水就是这个平均值。但是实际情况是有的地方雨多有的少,就引出了降水分布函数。
假设在雨区内布满了大小相同的N个雨量筒(成了如蜜蜂窝!)那么有的雨量筒收到的雨水多一些有的就少。经过观测和统计可以得到雨量分布函数[表(6)]。
表(6)不同的雨量(或者雨深)占了多少个雨量筒(面积)
| 雨量(以体积计算为v, 以雨深计算为r) | v1 |
v2 |
… |
vi |
… |
vq |
收到该雨量的雨量筒的个数 |
n1 |
n2 |
… |
ni |
… |
nq |
这个表把各地的雨量从最小v1到最大vq 分成了q个档次,并且列出了每个档次的降水有多少个雨量筒。由于每个雨量筒的横截面积相同,所以它的个数也就代表了面积的大小。
表中的雨量筒个数n1,n2..的合计值当然要与总的雨量筒个数N相等,于是有
![]() (1)
(1)
而总降水量V应当是各个雨量筒的雨量的合计值,即
![]() (2)
(2)
现在我们不急于回答如何从理论上得到多大的降水有多大的面积(各个vi对应于多少个雨量筒)的问题,转而考虑如下统计问题:
如果把N个雨量筒编上号,把总雨量V也分成N份[对每份的雨量的多少占不规定,但是要满足前面关系式(1),(2)]。从统计角度看每份雨水可能落在这个雨量筒也可能落到了另一个雨量筒。于是提出这样一个问题:N份雨水装入N 个雨量筒的方法有多少种?这如同剧场头排有30个位子要30人坐问有多少种坐法。在数学里这是N 个里取N 个的排列问题。答案是有N(N-1)(N-2)…3·2·1种安排方法。以!表示联乘积,就是有N!种方法。由此可见把V这么多雨水装入N个雨量筒的方法有很多种。
如果N个雨量筒中有n1个的雨量是相同的而其他的雨量都不相同,这意味着n1个雨量相同的雨量筒之间取消了自己的排列问题。由于n1个雨量筒的排列方法有n1!个。所以n1个雨量筒的雨量相同其他的各个雨量筒的雨量不同的排列方法应当是N!个方法中每有n1!个方法就退化为一个方法了。这只要把N!除以n1!就对了(n1<N)。即实现这种结局的方法应当有N!/ n1! 个。这相当于剧场头排30 个位子由30人坐虽然有30!种方法,但是30人中有5个人是一家人而且他们不计较具体坐在哪个位子上。于是真正不同的坐法仅有30!/5!。
依此类推如果实际的降水是
有n1个雨量筒的雨量相同,都是v1,并且
有n2个雨量筒的雨量相同,都是v2,并且
…
有nq个雨量筒的雨量相同,都是vq
那么实现这种结局的方法的个数 W 显然应当由下式计算
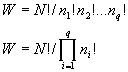 (3)
(3)
W 的这个公式有什么启发和用途呢?
上式表明W 是雨量筒总个数N 和各个档次的降水量分别占的雨量筒的个数的函数,即
![]()
它说明 n1,n2,…nq 的数值不同实现这种降水分布的可能方法的个数也不同。另外,由于不同雨量v1,v2…vq分别占有的不同的雨量筒数量n1,n2,…nq 对应了一个降水分布函数,所以不同的分布函数对应着有不同的W值(实现这种分布函数的方法有W个)。即实现某种分布函数的方法可能非常非常多而实现另外的分布函数的方法相比之下就极少。
在文献[5]中一个例子是某地区在100个雨量筒的面积上降了总量为1000的降水(平均雨量为10)。对四种降水分布函数计算了对应W的值(实现它们的办法有多少种),结果列于表(7)中
表(7)4种分布函数对应的实现办法(途径)的个数(W)差别非常大
A:每个地方的降水都是10(相同) |
W=1 |
B:99个雨量筒的雨量为99,另一个是109(合计是1000) |
W=100 |
C:50个雨量筒为5,另50个是15 |
|
D:使W值最大的那种分布函数 |
|
A 种分布(各地的降水相同)对应的方法数仅有1种,B是100种,C是![]() 种而 D是
种而 D是![]() 种(这种分布的计算方法后面谈)。这说明有的降水分布函数实现它的方法很少,有的实现它的方法非常非常多。
种(这种分布的计算方法后面谈)。这说明有的降水分布函数实现它的方法很少,有的实现它的方法非常非常多。
如果找不到什么理由说某种降水实现方法比其他的方法出现的概率更高,就假设大气中发生的降水过程中每个降水实现方法的出现概率都相同(这也正是统计力学中的一个基本假设)。结合求W 的公式我们看到如果每种方法实现的概率相同,由于有的分布函数仅对应一种实现方法,而有的分布函数对应非常多种的实现方法,最可能(有时统计力学书上称为最可几)出现的分布函数当然是 W 值最大的那一种分布函数。
这好似有一亿粒花生在袋子里让你任摸一个。袋子里99999990粒花生是好的,而另10粒有毛病。如果摸中任一粒花生的概率都相同,摸到好花生的概率就是99.99999%,它几乎就是100%。所以W值大的那一种分布函数出现的概率远比其他的分布函数出现的可能性高。统计力学中的玻尔兹曼统计的基本含义也就在这里[6,7]。
3.2求最可几的降水分布函数
既然不同的降水分布函数所对应的实现方案的数量(即W的值大小)差别很大,在每个实现方案出现的概率都相同的统计力学假设下就引出了W值最大的那一种分布函数是出现概率最高的(最可机的)结论。现在要利用这个结论从W最大反求它对应的降水分布函数(最可几分布)。
求函数的极大值是个纯数学问题,基本思路是令它对自变量的微商(偏微商)为零去求解。如果有一些约束条件要一起考虑,常用拉哥朗日乘子法[6](在大学理科的数学教科书中有介绍)。这里把具体推导过程[3]省略仅简单介绍有关的条件与结论。
求n1,n2…在什么值时W最大,要考虑到约束条件。本问题中的约束条件有两个。一个是各个ni的合计值应当等于N ,即满足公式(1)。另一个是所有雨量筒中的总雨量应当等于V ,即公式(2)应当满足。
在满足上述约束条件下如果让W的值最大(极大),那么ni 的值要与雨深ri的值保持如下关系:
![]() (4)
(4)
上式给出的是降水量在r到r+Δr 范围的雨量筒数量(因为雨量筒布满地面,它也代表了雨区面积ni 与平均雨量、总雨量筒数量的关系)。
令雨区总面积为A、一个雨量筒的截面积为ΔA ,则N=A/ΔA 。据此前面的公式变成
![]()
nΔA与AN的比值显然代表降水出现于r到r+Δr范围内的雨区占的相对面积。当Δr趋于零时公式左侧的含义应当是雨量在r处雨量每单位增量引起的相等面积的增加量。由于它是r的函数把它写成f(r)是合适的,于是有
![]() (5)
(5)
这就是雨量与面积相对关系的基本公式。它已经从离散型的公式变成了连续变量的公式了。公式左边表示降水每增加单位值时面积的相对(%)的增加量,右边说明这个增加量与降水量是负指数关系。即降水量大的占的相对面积小;降水量小的占的雨区的相对面积大(预告员早有这种定性经验,现在把这个经验提高到一个准确的公式)。
至此不仅把玻尔兹曼分析分子运动的统计力学思路引入了降水分析,也得出了雨量在面积上的分布函数。这个函数仅是众多个可能的分布函数中的一个,但是它却是最可能出现的哪个,在统计力学中称为最可几分布。本节说明了这个原理,后面会看到这个原理还可以用到其他的降水问题中。
---(1)部分结束---