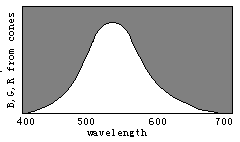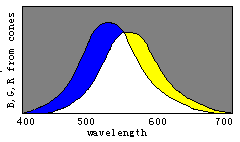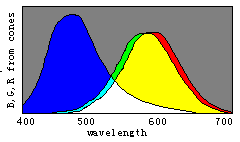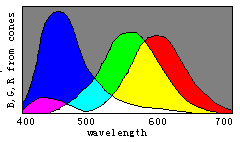
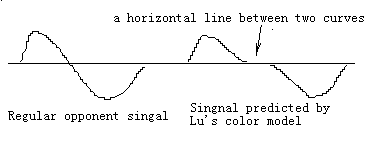
The right picture is the reversed one of the left picture. This shows that real opponet colors are Red/Cyan and Green/Magenta instead of Red/Green.
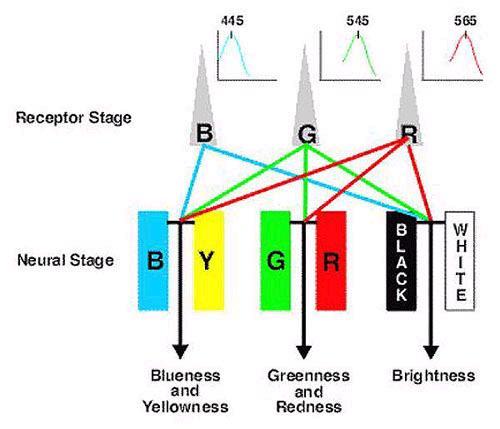
from http://webvision.med.utah.edu/KallColor.html
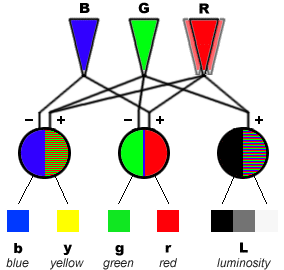
From http://www.handprint.com/HP/WCL/color1.html,Thanks.
The problem: G, R cannot be opponent or cannot compose white as indicated by Herring
(B,G,R)=(0,0,1) should be typical red color, there should be only output r>0. But The above model also yields y>0.
Problem: White can be produced without B or S signal--not compatible with Young-Helmholtz's theory and Color optics. The output r should be magenta otherwise r and g are not opponent.
(B,G,R)=(1,0,0) should be typical blue color. There should be only output b>0. But The above model also yields r>0.
(B,G,R)=c1*(0,0,1)+c2*(0,1,1)+....c7(1,1,1)
for example: (3,5,9)=3*(1,1,1)+2*(0,1,1)+4*(0,0,1)=3*white+2*yellow+4*red
Problem is how to get ci, i=1,2,...,7, which cannot be obtained only by additions and subtractions.
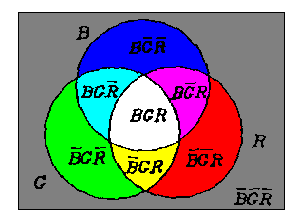
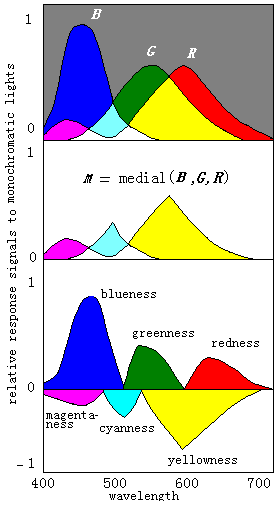
M=RGVRBVBG
R-M=RED/Cyan;G-N=Green/Magenta; B-M=Blue/Yellow
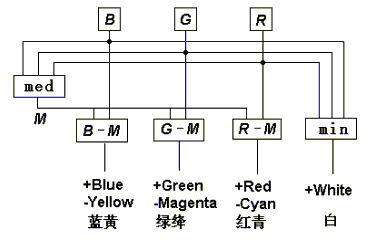
Continously logical operations:
M=middle(R,G,B)=max(min(R,G),min(R,B),min(R,B))
R-M=RED/Cyan;G-M=Green/Magenta; B-M=Blue/Yellow
กก
My explanation: michanism of color vision is evolving. Green/Magenta and Red/Cyan are not apart to much. So when we test opponent signals, we always confuse them each other.